[阿里筆試]以下是一個有向圖,我們從節點B開始進行深度優先遍歷(DFS),那麼以下5個序列中,所有正確的DFS序列是____。
題目(阿里筆試題):以下是一個有向圖,我們從節點B開始進行深度優先遍歷(DFS),那麼以下5個序列中,所有正確的DFS序列是__。
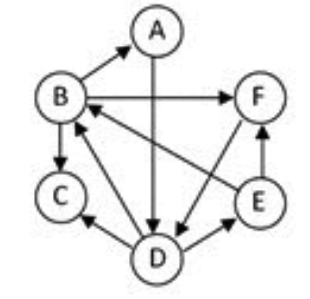
解析:深度優先遍歷是指優先探索完一條通路後才返回倒數第二個節點繼續探索另一條通路。如此往復直到所有節點都遍歷結束。答案A
相關推薦
[阿里筆試]以下是一個有向圖,我們從節點B開始進行深度優先遍歷(DFS),那麼以下5個序列中,所有正確的DFS序列是____。
題目(阿里筆試題):以下是一個有向圖,我們從節點B開始進行深度優先遍歷(DFS),那麼以下5個序列中,所有正確的DFS序列是__。 解析:深度優先遍歷是指優先探索完一條通路後才返回倒數第二個節點繼
【圖的遍歷】廣度優先遍歷(DFS)、深度優先遍歷(BFS)及其應用
bsp 及其 spa (第五版 family 實驗 條件 soft 深度優先遍歷算法 無向圖滿足約束條件的路徑 • 目的:掌握深度優先遍歷算法在求解圖路徑搜索問題的應用 內容:編寫一個程序,設計相關算法,從無向圖G中找出滿足如下條件的所有路徑 (1)給定
各種圖的創建以及廣度,深度優先遍歷(臨接矩陣存儲)
visit pos code cell stream 相關 pri inpu mar #include <stdio.h> #include <iostream> #include <limits.h> #include <
圖的深度優先遍歷(非遞迴+遞迴,詳解)
圖的深度優先遍歷 非遞迴演算法: #include<iostream> #include<stack> using namespace std; const int MaxSize=100; class MGraph{//鄰接矩陣的構建 p
圖的深度優先遍歷(鄰接矩陣,遞迴,非遞迴)
參考部落格:圖的深度優先遍歷(遞迴、非遞迴;鄰接表,鄰接矩陣) 本篇預設連通圖,非連通情況會在鄰接表處補上 1.鄰接矩陣的遞迴解法 #include<stdio.h> #define MAX 100 typedef struct { int e[MAX][MA
圖的深度優先遍歷(鄰接表,遞迴,非遞迴)
參考部落格:圖的深度優先遍歷(遞迴、非遞迴;鄰接表,鄰接矩陣) 本程式碼有個問題:就是結點是對應儲存下標的,要解決這個問題,可以增加一個定位函式(LocateVec),不修改也可以使程式碼簡潔些 關於非連通圖的bug已修改,就是增加了dfsTraverse函式迴圈遍歷一遍結點:沒訪問過則再做一次dfs
圖相關演算法(二):無向無權圖的廣度優先遍歷(BFS)-非遞迴版本
核心 採用鄰接表作為圖資料的儲存結構 對訪問過的節點進行記錄,文中採用HashSet實現 採用佇列存放未訪問的子節點,不斷更新佇列 BFS採用佇列實現很簡單,採用遞迴反而更復雜了 本文建立的圖結構如
6-1 鄰接矩陣儲存圖的深度優先遍歷 (20 分)
試實現鄰接矩陣儲存圖的深度優先遍歷。 函式介面定義: void DFS( MGraph Graph, Vertex V, void (*Visit)(Vertex) ); 其中MGraph是鄰接矩陣儲存的圖,定義如下: typedef struct GNode *PtrToG
6-1 鄰接矩陣儲存圖的深度優先遍歷 (20 分) 第七章--圖--基本概念-計算機17級
6-1 鄰接矩陣儲存圖的深度優先遍歷 (20 分) 試實現鄰接矩陣儲存圖的深度優先遍歷。 函式介面定義: void DFS( MGraph Graph, Vertex V, void (*Visit)(Vertex) ); 其中MGraph是鄰接矩陣儲存的圖
1-7 鄰接矩陣儲存圖的深度優先遍歷 (10 分)
試實現鄰接矩陣儲存圖的深度優先遍歷。 函式介面定義: void DFS( MGraph Graph, Vertex V, void (*Visit)(Vertex) ); 其中MGraph是鄰接矩陣儲存的圖,定義如下: typedef struct GNode *PtrToGNod
圖的深度優先遍歷(DFS)和廣度優先遍歷(BFS)
1 建立測試圖(鄰接矩陣和鄰接表儲存形式) 首先建立一個圖用於後續程式碼的測試,在此以無向圖為例,且所有邊的權值都為1。儲存方式分別為鄰接矩陣和鄰接表(見上一篇介紹) 鄰接矩陣: class Graph{ constructor(v,vr){ let len = v.le
C++實現圖的鄰接矩陣的建立以及其深度優先遍歷和廣度優先遍歷
#include<iostream> using namespace std; typedef char vertextype; typedef int edgetype; #define maxvex 100 #define infinity 1000 #in
圖的深度優先遍歷(DFS)和廣度優先遍歷(BFS)--解析
圖的資料結構不像二叉樹那樣,有明顯的父子節點和兄弟節點的關係,它只有一個關係就是鄰接關係。故對圖中頂點的訪問要採用標誌陣列(來確定改結點是否被訪問,去除重複訪問)。並且對圖的深度遍歷採用遞迴的方式是較高效的。 1.深度遍歷(DFS) #include<iostream
6-1 鄰接矩陣儲存圖的深度優先遍歷 (20 分) 第七章--圖--基本概念-計算機17級
6-1 鄰接矩陣儲存圖的深度優先遍歷 (20 分) 試實現鄰接矩陣儲存圖的深度優先遍歷。 函式介面定義: void DFS( MGraph Graph, Vertex V, void (*Visi
圖的深度優先遍歷(DFS)和廣度優先遍歷(BFS)
概述 圖的遍歷是指從圖中的任一頂點出發,對圖中的所有頂點訪問一次且只訪問一次。圖的遍歷操作和樹的遍歷操作功能相似。圖的遍歷是圖的一種基本操作,圖的其它演算法如求解圖的連通性問題,拓撲排序,求關鍵路徑等都是建立在遍歷演算法的基礎之上。 由於圖結構本身
Toposort Description 給出一個有向圖,判斷圖中是否存在迴路。 Input: 第1行:輸入圖的頂點個數N(1 ≤ N≤ 2,500)和C(圖的邊數,1 ≤ C ≤ 6,20
Toposort Description 給出一個有向圖,判斷圖中是否存在迴路。 Input: 第1行:輸入圖的頂點個數N(1 ≤ N≤ 2,500)和C(圖的邊數,1 ≤ C ≤ 6,200); 第2到C+1行中,第i+1行輸入兩個整數,分別表示第i條邊的起點和終點的編號
建立有向圖的鄰接表,深度優先遍歷和廣度優先遍歷的遞迴與非遞迴演算法,判斷是否是有向無環圖,並輸出一種拓撲序列
/*(1)輸入一組頂點,建立有向圖的鄰接表,進行DFS(深度優先遍歷)和BFS(廣度優先遍歷)。 寫出深度優先遍歷的遞迴和非遞迴演算法。 (2)根據建立的有向圖,判斷該圖是否是有向無環圖,若是,則輸出其一種拓撲有序序列。*/ #include<stdio.h>
給定一個有向圖,問從A點恰好走k步(允許重複經過邊)到達B點的方案數---矩陣乘法
#include <iostream> #include <cstdio> #include <algorithm> #include <cmath>
求一個有向圖G的拓撲序列
題目:已知有向圖G=(V,E),其中V={V1,V2,V3,V4,V5,V6,V7},E={(V1,V2),(V1,V3),(V1,V4),(V2,V5),(V3,V5),(V3,V6),(V4,V6
uva11090 給你一個有向圖,求出平均權值最小的環
B 【題目描述】 泡泡魚是一條調皮的魚,ta 的家住在一片珊瑚礁上。在 ta 的眼裡,這些珊瑚礁的形態 可以腦補成一個 n 個節點,m 條邊的帶權圖,在海水的腐蝕下,這些珊瑚礁形成了許多的 環,ta 想考考你能不能找出這些環中,權值的平均值最小的環。泡泡魚這麼聰明,ta
