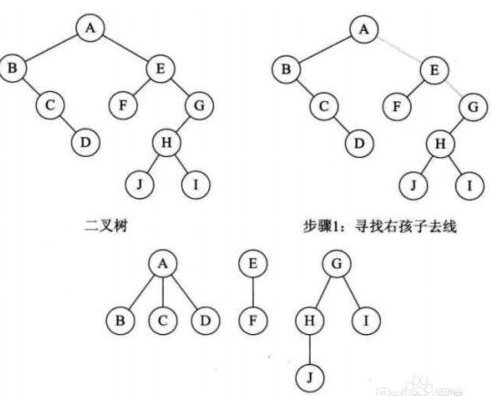
coding A&D:森林與二叉樹的轉換
首先,樹轉二叉樹:
「1」兄弟+橫線
樹中的每一個結點,如果該結點有兄弟結點,那麼就在這幾個兄弟結點之間進行連線。
「2」儲存長子線
對於樹中的每一個結點,如果其有多個子節點,儲存其第一個子節點的連線,去除其他子節點的連線。
「3」調整位置
對每個結點調整一定的位置,使其符合二叉樹的標準。
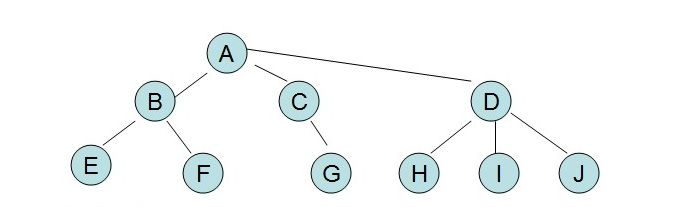
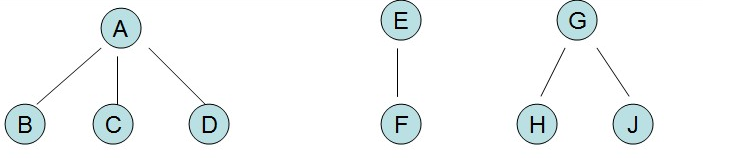
1. 森林轉換為二叉樹
【1】將每課樹轉換成二叉樹
【2】將每課樹的根結點連線起來
【3】把每棵樹的根當做兄弟結點處理,兄弟加橫線旋轉調整位置
「例題」
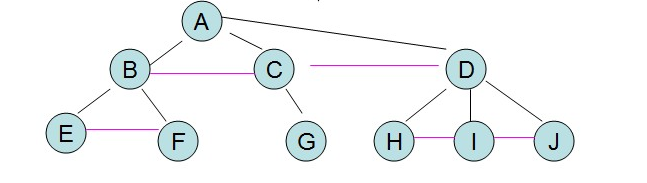
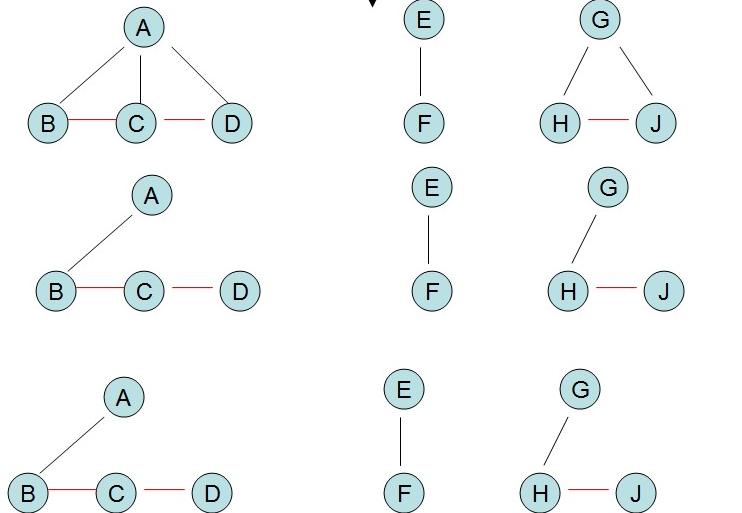
【1】將每課樹轉換成二叉樹
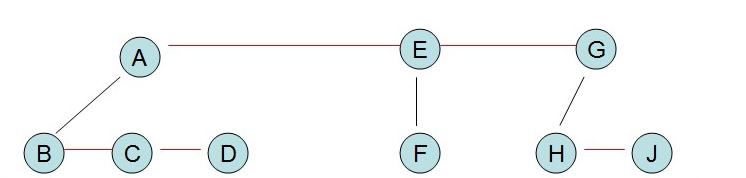
【2】根結點橫線連線
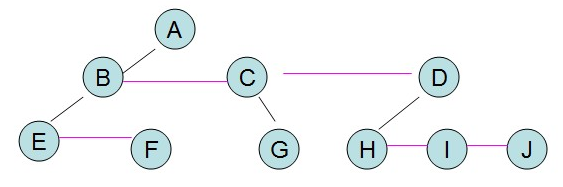
【3】調整位置,橫線變斜線
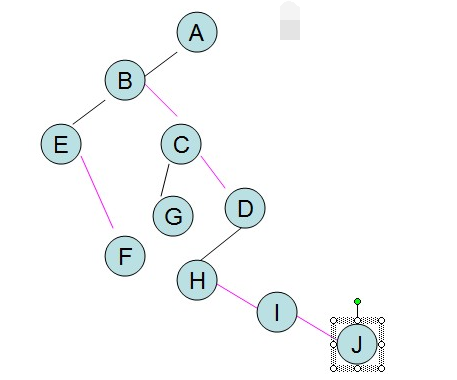
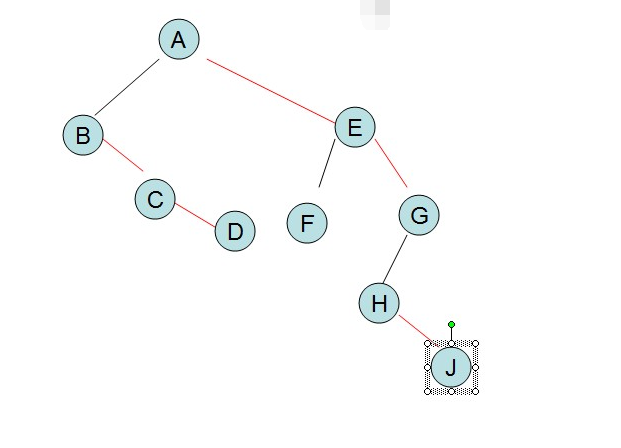
2.二叉樹轉化為森林:
【1】根+左子樹,根+左子樹,... ...
【2】調整位置
相關推薦
coding A&D:森林與二叉樹的轉換
首先,樹轉二叉樹: 「1」兄弟+橫線 樹中的每一個結點,如果該結點有兄弟結點,那麼就在這幾個兄弟結點之間進行連線。 「2」儲存長子線 對於樹中的每一個結點,如果其有多個子節點,儲存其第一個子節點的連線,去除其他子節點的連線。 「3」調整位置 對每個結點
coding A&D:AVL平衡二叉樹的旋轉(插入結點)
【1】AVL平衡二叉樹的基本概念: 平衡二叉樹建立在二叉排序樹的基礎上,目的是使二叉排序樹的平均查詢長度更小,即讓各結點的深度儘可能小,因此,樹中每個結點的兩棵子樹的深度不要偏差太大。 平衡二叉樹的遞迴定義:平衡二叉樹是一棵二叉樹,其可以為空,或滿足如下2個性質:①左右子
資料結構與演算法12-樹、森林與二叉樹的轉換
樹和森林的二叉樹轉換 對於樹來說,在滿足樹的條件下可以是任意開頭,一個結點可以有任意多個孩子,顯然對樹的處理要複雜得多,去研究關於樹的性質和演算法,真的不容易。有沒有簡單的方法來處理樹呢?當然有啦~ 前面我們提到過的樹的孩子兄弟法可以將一棵樹用二叉連結串列進行儲存,所以藉助二叉連結串列,樹和
樹、森林與二叉樹的相互轉換
eight inf http 轉換 alt 森林 技術分享 分享 相互 樹、森林與二叉樹的相互轉換
樹、森林與二叉樹的轉換總結
前言: 在樹這一塊的資料結構中最重要的就是二叉樹,但是對於我們大部分人來說二叉樹的基礎掌握還是ok的,但是有時候我們也會忽略了樹於森林(本人就是忽略了),今天就在這裡總結總結數、森林與二叉樹的轉換
資料結構——樹、森林與二叉樹的轉換
在介紹樹的儲存結構時,就說到了樹的孩子兄弟表示法可以將一棵樹用二叉連結串列進行儲存,所以藉助二叉連結串列,樹和二叉樹可以互相轉換。從物理結構上來看,它們的二叉連結串列也是相同的,只是介紹不太一樣而已。因此,只要我們設定一定的規則,用二叉樹來表示樹,甚至表示森林都
樹、森林與二叉樹的轉換
由於二叉樹和樹都可以用二叉連結串列作為儲存結構,則以二叉連結串列作為媒介可以匯出樹與二叉樹的一個對應關係,即給定一棵樹,可以找到唯一的一顆二叉樹與之對應。從物理結構上看,樹的孩子兄弟表示法語二叉樹的二叉連結串列表示法相同,即每個結點共有兩個指標,分別指向結點
樹、森林與二叉樹相互轉化
1、樹轉換為二叉樹由於二叉樹是有序的,為了避免混淆,對於無序樹,我們約定樹中的每個結點的孩子結點按從左到右的順序進行編號。將樹轉換成二叉樹的步驟是:(1)加線。就是在所有兄弟結點之間加一條連線;(2)抹線。就是對樹中的每個結點,只保留他與第一個孩子結點之間的連線,刪除它與其它孩子結點之間的連線;(3)旋轉。就
森林與二叉樹的轉換
1、森林轉二叉樹 (1)、把每棵樹轉換為二叉樹 (2)、第一棵二叉樹不動,從第二棵二叉樹開始,一次把後一棵二叉樹的根結點作為前一棵二叉樹的根結點的右孩子,用線連線起來。 轉換規則:兄弟相連,長兄為父,孩子靠左。 2、樹轉二叉樹 (1)、加線。在所有的兄弟
coding A&D:圖:最小生成樹(二):破圈法
求MST的演算法中,prim演算法和kruskal演算法思想是:“加邊”; 破圈法正好相反,破圈即為:“減邊”。 破圈法是一種貪心演算法,思想大體如下: 1.找到圖中的一個圈; 2.刪除其中的權最大的邊; 3.重複上述操作,直到圖中已無圈。 以下為bd百科中的
森林、樹與二叉樹相互轉換
節點 png http 所有 相互轉換 層次 二叉樹 根節點 images 1、森林轉二叉樹 (1)、把每棵樹轉換為二叉樹 (2)、第一棵二叉樹不動,從第二棵二叉樹開始,一次把後一棵二叉樹的根結點作為前一棵二叉樹的根結點的右孩子,用線連接起來。
實驗四:樹與二叉樹的實驗一
一、實驗目的1、 熟練理解樹和二叉樹的相關概念,掌握的儲存結構和相關操作實現;2、 掌握樹的順序結構的實現;3、 學會運用樹的知識解決實際問題二、實驗內容 自己確定一個二叉樹(樹結點型別、數目和結構自定)利用順序結構方法儲存。實現樹的構造,並完成:1) 層序輸出結點資料;2) 以合理的格式
coding A&D:關鍵路徑(AOE網)
1、AOE-網介紹 我們在學習拓撲排序(如果沒學,可以看看這篇部落格:拓撲排序詳解)的時候,已經接觸了什麼是AOV-網,AOV-網是優先考慮頂點的思路,而我們也同樣可以優先考慮邊,這個就是AOE-網的思路。 若在帶權的有向無環圖中,以頂點表示事件,以有向邊表示活
coding A&D:(選擇排序)堆排序
【概念】: 堆是具有以下性質的完全二叉樹: 每個結點的值都大於或等於其左右孩子結點的值,稱為大根堆; 或者每個結點的值都小於或等於其左右孩子結點的值,稱為小根堆。 (注意:這種結構是對父節點-左/右孩子節點之間做的約束,而對左-右孩子節點之間並沒有什麼
coding A&D:KMP演算法
一些演算法、資料結構長時間不用,就忘記了,甚至連概念都忘了,最麻煩的是忘記當初如何理解該概念的方法了。。。 瀏覽部落格時發現這兩位博主的博文有助於我重新理解kmp演算法,遂參考一下,進行總結,有助於以後使用: 總結如下: 【概念】:首先KMP是用來進行串的模
資料結構:二分查詢與二叉樹
關於二分查詢,原理其實不難,而且java Arrays類裡面有一個sorts()方法,可以先對資料進行排序,然後呼叫binarySerarch()方法,這個方法就是進行二分查詢用的。 下面是JDK的原始碼: private static int binarySe
coding A&D:計算雜湊表
例題(來源:2010年全國統考專業課408 第一題) 一. 雜湊表—線性探測法的ASL成功、不成功計算 將關鍵字序列(7、8、30、11、18、9、14)雜湊儲存到散列表中。散列表的儲存空間是一個下標從0開始的一維陣列。雜湊函式為: H(key) = (keyx3) MOD
#資料結構與演算法學習筆記#劍指Offer35:是否平衡二叉樹/AVL樹 + 測試用例(Java、C/C++)
2018.11.3 前幾天有用遞迴實現了二叉樹的深度#資料結構與演算法學習筆記#劍指Offer36:二叉樹的深度(Java),因此可以對每個結點先序遍歷進行一次平衡驗證,只要確定每個結點都是平衡的
coding A&D:最短路徑
最短路徑問題分為兩大類: #無勸圖的單源最短路徑; #帶權有向圖的單源最短路徑、各頂點之間的最短路徑。 求解最短路徑的演算法,通常都依賴於一種性質,也就是兩點之間的最短路徑也包含了路徑上其他頂點間的最短路徑 【1】無權圖的單源最短路徑: 可用BFS廣度優先搜尋;
C/C++:各種基本演算法實現小結(三)—— 樹與二叉樹
各種基本演算法實現小結(三)—— 樹與二叉樹 (均已測試通過) =================================================================== 二叉樹——先序 測試環境:VC 6.0 (C