淺顯易懂, 清楚明白, 入門之佳品, 菜鳥之福音.

轉者注:

在實際應用中, 並不實施 "以一定的概率接受較差的移動", 而是以 "在全域性範圍內隨機試探多個點, 再在每個點的鄰域內隨機試探多個點, 得到該鄰域內極值, 最終取多個點的最大(最小)值"  的方式避免最終得到區域性最優解. 這種處理其實拋棄了模擬退火的核心思想(來源於退火中溫差和降溫速率關係的計算概率的公式), 但是效果明顯優於原先. 

有種說法叫"隨機化變步長貪心法", 或許那些聲稱是"模擬退火"的題本來就不是真正的模擬退火...? 總之前者好用就對了~

===

一. 爬山演算法 ( Hill Climbing )

         介紹模擬退火前，先介紹爬山演算法。爬山演算法是一種簡單的貪心搜尋演算法，該演算法每次從當前解的臨近解空間中選擇一個最優解作為當前解，直到達到一個區域性最優解。

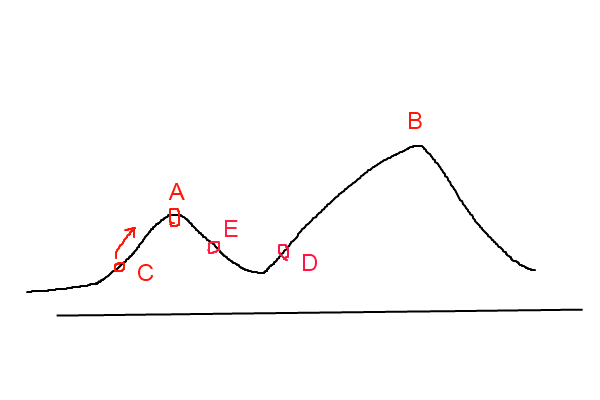
         爬山演算法實現很簡單，其主要缺點是會陷入區域性最優解，而不一定能搜尋到全域性最優解。如圖1所示：假設C點為當前解，爬山演算法搜尋到A點這個區域性最優解就會停止搜尋，因為在A點無論向那個方向小幅度移動都不能得到更優的解。

圖1

二. 模擬退火(SA,Simulated Annealing)思想

         爬山法是完完全全的貪心法，每次都鼠目寸光的選擇一個當前最優解，因此只能搜尋到區域性的最優值。模擬退火其實也是一種貪心演算法，但是它的搜尋過程引入了隨機因素。模擬退火演算法以一定的概率來接受一個比當前解要差的解，因此有可能會跳出這個區域性的最優解，達到全域性的最優解。以圖1為例，模擬退火演算法在搜尋到區域性最優解A後，會以一定的概率

         模擬退火演算法描述：

         若J( Y(i+1) )>= J( Y(i) )  (即移動後得到更優解)，則總是接受該移動

         若J( Y(i+1) )< J( Y(i) )  (即移動後的解比當前解要差)，則以一定的概率接受移動，而且這個概率隨著時間推移逐漸降低（逐漸降低才能趨向穩定）

　　這裡的“一定的概率”的計算參考了金屬冶煉的退火過程，這也是模擬退火演算法名稱的由來。

　　根據熱力學的原理，在溫度為T時，出現能量差為dE的降溫的概率為P(dE)，表示為：

　　　　P(dE) = exp( dE/(kT) )

　　其中k是一個常數，exp表示自然指數，且dE<0。這條公式說白了就是：溫度越高，出現一次能量差為dE的降溫的概率就越大；溫度越低，則出現降溫的概率就越小。又由於dE總是小於0（否則就不叫退火了），因此dE/kT < 0 ，所以P(dE)的函式取值範圍是(0,1) 。

　　隨著溫度T的降低，P(dE)會逐漸降低。

　　我們將一次向較差解的移動看做一次溫度跳變過程，我們以概率P(dE)來接受這樣的移動。

　　關於爬山演算法與模擬退火，有一個有趣的比喻：

　　爬山演算法：兔子朝著比現在高的地方跳去。它找到了不遠處的最高山峰。但是這座山不一定是珠穆朗瑪峰。這就是爬山演算法，它不能保證區域性最優值就是全域性最優值。

　　模擬退火：兔子喝醉了。它隨機地跳了很長時間。這期間，它可能走向高處，也可能踏入平地。但是，它漸漸清醒了並朝最高方向跳去。這就是模擬退火。

下面給出模擬退火的偽程式碼表示。

三. 模擬退火演算法虛擬碼

/*
 *  J(y)：在狀態y時的評價函式值
 *  Y(i)：表示當前狀態
 *  Y(i+1)：表示新的狀態
 *  r： 用於控制降溫的快慢
 *  T： 系統的溫度，系統初始應該要處於一個高溫的狀態
 *  T_min ：溫度的下限，若溫度T達到T_min，則停止搜尋
*/

while( T > T_min )
{
　　dE = J( Y(i+1) ) - J( Y(i) ) ;  

　　if ( dE >= 0 )  //表達移動後得到更優解，則總是接受移動
        Y(i+1) = Y(i) ;  //接受從Y(i)到Y(i+1)的移動
　　else
　　{
    // 函式exp( dE/T )的取值範圍是(0,1) ，dE/T越大，則exp( dE/T )也
        if ( exp( dE/T ) > random( 0 , 1 ) )
            Y(i+1) = Y(i) ;  //接受從Y(i)到Y(i+1)的移動
　　}
　　T = r * T ;  //降溫退火 ，0<r<1 。r越大，降溫越慢；r越小，降溫越快
　　/*
　　* 若r過大，則搜尋到全域性最優解的可能會較高，但搜尋的過程也就較長。若r過小，則搜尋的過程會很快，但最終可能會達到一個區域性最優值
　　*/
　　i ++ ;
}

四. 使用模擬退火演算法解決旅行商問題

　　旅行商問題 ( TSP , Traveling Salesman Problem ) ：有N個城市，要求從其中某個問題出發，唯一遍歷所有城市，再回到出發的城市，求最短的路線。

　　旅行商問題屬於所謂的NP完全問題，精確的解決TSP只能通過窮舉所有的路徑組合，其時間複雜度是O(N!) 。

　　使用模擬退火演算法可以比較快的求出TSP的一條近似最優路徑。（使用遺傳演算法也是可以的，我將在下一篇文章中介紹）模擬退火解決TSP的思路：

1. 產生一條新的遍歷路徑P(i+1)，計算路徑P(i+1)的長度L( P(i+1) )

2. 若L(P(i+1)) < L(P(i))，則接受P(i+1)為新的路徑，否則以模擬退火的那個概率接受P(i+1) ，然後降溫

3. 重複步驟1，2直到滿足退出條件

　　產生新的遍歷路徑的方法有很多，下面列舉其中3種：

1. 隨機選擇2個節點，交換路徑中的這2個節點的順序。

2. 隨機選擇2個節點，將路徑中這2個節點間的節點順序逆轉。

3. 隨機選擇3個節點m，n，k，然後將節點m與n間的節點移位到節點k後面。

五. 演算法評價

        模擬退火演算法是一種隨機演算法，並不一定能找到全域性的最優解，可以比較快的找到問題的近似最優解。 如果引數設定得當，模擬退火演算法搜尋效率比窮舉法要高。