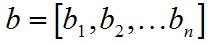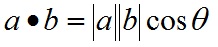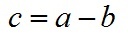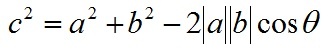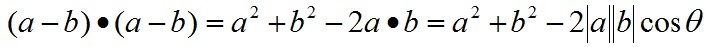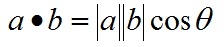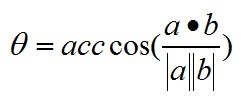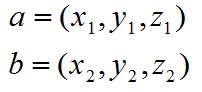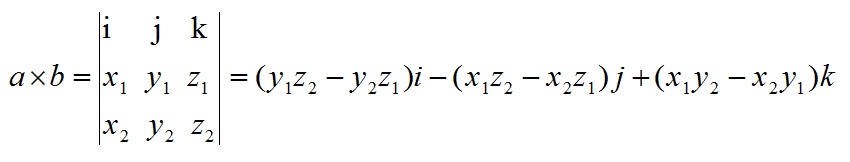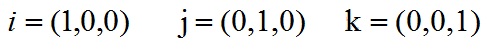宣告： 本文轉自這裡

向量是由n個實陣列成的一個n行1列（n*1）或一個1行n列（1*n）的有序陣列；

向量的點乘,也叫向量的內積、數量積，對兩個向量執行點乘運算，就是對這兩個向量對應位一一相乘之後求和的操作，點乘的結果是一個標量。

點乘公式

對於向量a和向量b：

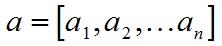
a和b的點積公式為：

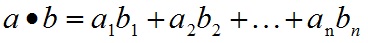
要求一維向量a和向量b的行列數相同。

點乘幾何意義

點乘的幾何意義是可以用來表徵或計算兩個向量之間的夾角，以及在b向量在a向量方向上的投影

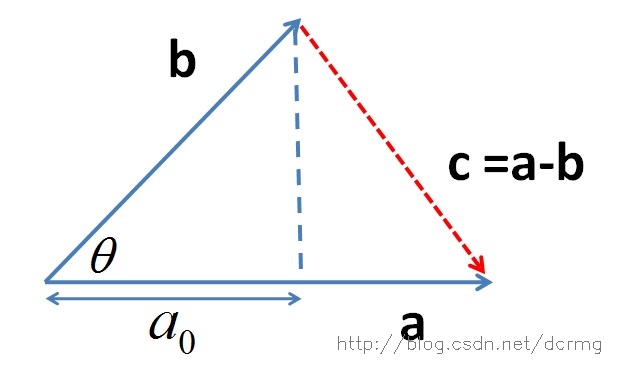
推導過程如下，首先看一下向量組成：

定義向量：

根據三角形餘弦定理有：

根據關係c=a-b（a、b、c均為向量）有：

即：

向量a，b的長度都是可以計算的已知量，從而有a和b間的夾角θ：

根據這個公式就可以計算向量a和向量b之間的夾角。從而就可以進一步判斷這兩個向量是否是同一方向，是否正交(也就是垂直)等方向關係，具體對應關係為：

     a·b>0    方向基本相同，夾角在0°到90°之間

     a·b=0    正交，相互垂直  

     a·b<0    方向基本相反，夾角在90°到180°之間 

叉乘公式

兩個向量的叉乘，又叫向量積、外積、叉積，叉乘的運算結果是一個向量而不是一個標量。並且兩個向量的叉積與這兩個向量組成的座標平面垂直。

對於向量a和向量b：

a和b的叉乘公式為：

其中：

根據i、j、k間關係，有：

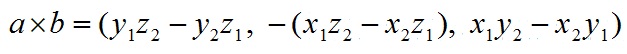
叉乘幾何意義

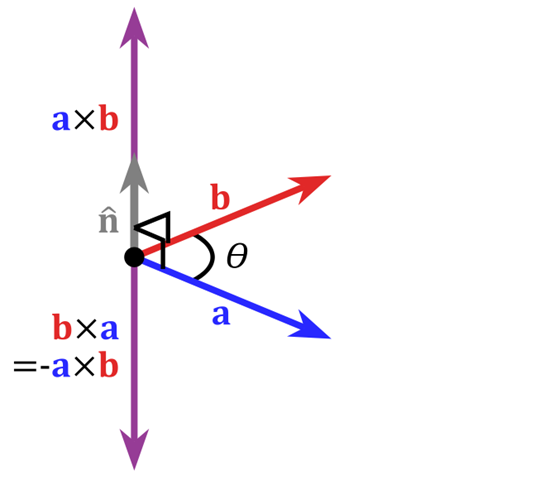
在三維幾何中，向量a和向量b的叉乘結果是一個向量，更為熟知的叫法是法向量，該向量垂直於a和b向量構成的平面。

在3D影象學中，叉乘的概念非常有用，可以通過兩個向量的叉乘，生成第三個垂直於a，b的法向量，從而構建X、Y、Z座標系。如下圖所示： 

在二維空間中，叉乘還有另外一個幾何意義就是：aXb等於由向量a和向量b構成的平行四邊形的面積。