資料結構(六)-圖(二)--演算法篇
圖-常用演算法
4. 圖的連通性問題
在無向圖中,如果無向圖是連通圖,僅需從任意一點出發,進行深度優先搜尋或廣度優先搜尋,邊可訪問到圖中所有頂點。對非連通圖,則多個頂點出發進行搜尋,而每一次從一個新的起始點出發進行搜尋過程中得到的頂點訪問序列恰為其各個連通分量中的頂點集。
在有向圖中,儘可能多的若干頂點組成的子圖中,這些頂點都是相互可到達的,則這些頂點成為一個強連通分量。
由於無向圖中求解連通分量只用DFS即可,下面重點討論一下強連通分量如何求解。
4.1 有向圖的強連通分量
有向圖的強連通分量求解方法其實和無向圖求解方法類似,均是利用了DFS。具體步驟分為兩步:
- 從任意節點出發,對該節點進行DFS遍歷,將遍歷過程放入堆疊中,最後將出棧順序取反。
- 依次逆DFS上述步驟得到的取反出棧順序序列,每次DFS即可得一個強連通分量。
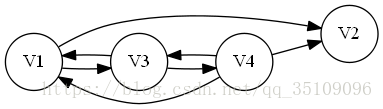
下面以一個例項來進行說明:
按照演算法步驟:
- 從V1開始遍歷,先入棧v1,再入棧v2,v2出,在入棧v3,最後入棧v4,最後v4,v3,v1呼喊。現在棧的出棧順序為(v2,v4,v3,v1)。。
- 從得到的序列從後向前(如開始取v1)開始逆DFS遍歷,有v1->v3->v4,無法在繼續遍歷。所以從剩下的點(剩下v2)開始逆DFS,得到v2。
綜上,有兩個強連通分量,分別為(v1,v3,v4)和(v2)。
那麼程式碼如何實現呢,首先應該考慮使用什麼樣的資料結構,方便實現。前一篇文章中,共提到4中儲存結構,分別是–鄰接矩陣,鄰接表,十字連結串列,鄰接多重表。注意到在整個演算法中,既要前向DFS,也要反向DFS,也即需要方便知道任意節點有哪些入度邊,有哪些出度邊。所以十字連結串列
//
// Created by Raven on 2018/8/3.
//
/**
* 連通分量的求解。
* 無向圖:直接DFS
* 有向圖:兩次DFS+堆疊
*/
#include <stack>
#include <vector>
#include <algorithm>
#include "Public.h"
//---------------資料結構採用:十字連結串列------------
#define MAX_NODES_NUM 20
typedef struct ArcNode {
int 4.2 最小生成樹
現在有這樣一種需求:假設要再n個城市之間建立通訊聯網網,則連通n個城市之需要n-1條線路。這時,產生了一個問題,如何才能在最節省經費的前提下建立這個通訊網?這就是最小生成樹的作用了。常用的演算法有兩種,Prim演算法(從節點出發,進行生成),Kruskal演算法(從邊出發,進行生成)。
下面貼出完整程式碼:
4.2.1 Prim演算法
//
// Created by Raven on 2018/8/1.
//
#include <vector>
#include "Public.h"
/**
* 最小生成樹-prim演算法
*/
#define MAX_VALUE 1000
const int N = 6;
int adj[N][N] = {
{0, 6, 1, 5, 0, 0},
{6, 0, 5, 0, 3, 0},
{1, 5, 0, 5, 6, 4},
{5, 0, 5, 0, 0, 2},
{0, 3, 6, 0, 0, 6},
{0, 0, 4, 2, 6, 0}
};
bool visted[N];
bool allAdded() {
return visted[0] & visted[1] & visted[2] & visted[3]
& visted[4] & visted[5];
}
int main(void) {
vector<int> v; //選點序列
v.push_back(0); //假設從0開始
visted[0] = true;
while (!allAdded()) {
int index = -1; //記錄本次迴圈中最小的點
int minValue = MAX_VALUE;
for (vector<int>::iterator iter = v.begin(); iter < v.end(); iter++) {
int p = *iter;
for (int i = 0; i < N; i++) {
if (!visted[i] && adj[i][p]) {
if (minValue > adj[i][p]) {
index = i;
minValue = adj[i][p];
}
}
}
}
visted[index] = true;
v.push_back(index);
}
for (int i : v) {
cout << i << " " ;
}
return 0;
}4.2.2 Kruskal演算法
//
// Created by Raven on 2018/8/1.
//
#include <vector>
#include "Public.h"
/**
* 最小生成樹:克魯斯卡爾演算法
*/
typedef struct{
int start;
int end;
int weight;
}Edge;
/**
* 簡單選擇排序
* @param edge
* @param e
*/
void sort(Edge edge[],int e){
for(int i = 0;i<e-1;i++){
for(int j = i;j<e;j++){
if(edge[i].weight > edge[j].weight){
Edge temp = edge[i];
edge[i] = edge[j];
edge[j] = temp;
}
}
}
}
//---------------並查集------------
/**
* 由於K演算法中要判定是否成環,所以需要使用到並查集
*/
/**
* 找到集合的根節點
* @param S
* @param e 本集合中的其中一個節點
* @return
*/
ElemType findParent(ElemType S[], ElemType e) {
ElemType x = e;
while (x != S[x]) {
x = S[x];
}
//路徑壓縮
ElemType root = x;
x = e;
while (x != S[x]) {
S[x] = root;
x = S[x];
}
return root;
}
/**
* 判定是否是同一節點
* @param S 儲存所有節點資訊(雙親節點)
* @param e1 元素1
* @param e2 元素2
* @return
*/
bool isSameSet(ElemType S[], ElemType e1, ElemType e2) {
if (findParent(S, e1) == findParent(S, e2)) {
return TRUE;
} else {
return FALSE;
}
}
/**
* 合併集合
* @param S
* @param e1
* @param e2
*/
void merge(ElemType S[], ElemType e1, ElemType e2) {
ElemType root1 = findParent(S, e1);
ElemType root2 = findParent(S, e2);
S[root1] = root2;
}
/**
* 輸入:
* n個點,e條邊
* 接下來e行,每行3個數,i,j,w。代表i->j這條邊,權重為w
* 輸入樣例:
* 9
* 0 1 6
* 0 2 1
* 0 3 5
* 1 2 5
* 1 4 3
* 2 3 5
* 2 4 6
* 2 5 4
* 4 5 6
* 輸出樣例
* @return
*/
int main(void){
int n,e;
cin>>n>>e;
Edge edges[e];
for(int i = 0;i<e;i++){
cin>>edges[i].start>>edges[i].end>>edges[i].weight;
}
//排序
sort(edges,e);
//K演算法
vector<Edge> v; //裝入邊序列
int S[n]; //並查集
for(int i = 0;i<S[n];i++) S[i] = i; //初始並查集,最開始各自為一個集合
int k = 1; //指向當前將要取出的指標
v.push_back(edges[0]);
while(v.size() != n-1){
Edge p = edges[k++];
//判斷是否與以選擇的邊構成環
if(!isSameSet(S,p.start,p.end)){
merge(S,p.start,p.end);
v.push_back(p);
}
}
for(Edge c :v){
cout<<"start="<<c.start<<" end="<<c.end<<" weight="<<c.weight<<endl;
}
return 0;
}
4.3 關節點
學習過“通訊網理論基礎”的朋友應該知道割端集的概念,關節點其實就是割點。當然沒有學習過的朋友,下面我給出它的定義:假設在刪去頂點v以及和它相關聯的各邊之後,將圖的一個聯通分量分割成兩個或兩個以上的連通分量,則稱頂點v為該圖的一個關節點。關節點有重要意義,如在戰爭中,破壞敵軍的運輸關節點,可使對方運輸中斷。沒有關節點的圖其連通性必然較好,更為健壯。那麼如何去求解一個圖中的關節點呢?
其中最重要的有兩句話與一個公式(在我的程式碼中也有詳盡的註釋)
- 若生成樹的根有兩顆或兩顆以上的子樹,則次根節點必為關節點。
- 若生成樹中某個非葉子頂點v,其某顆子樹的根和子樹中的其他節點均沒有指向v的祖先的回邊,則v為關節點。
以及一個公式:
其中:
- w為v的孩子節點
- k為v的父親節點
- low[v] 代表 v能回溯到的最高層節點
- visited[v] 代表樹的前序遍歷的次序
判決一個點是否為關節點的條件為:
如果成立,則v一定是關節點,反之則不是。
下面是完整程式碼:
//
// Created by Raven on 2018/8/1.
//
#include "Public.h"
/**
* 尋找關節點(割點)演算法
* 公式:
* low[v] = min{visited[v],low[w],visited[k]}
* w為v的孩子節點
* k為v的父親節點
* 判決條件:
* low[w]>=visited[v]
* 說明:
* low[v] 代表 v能回溯到的最高層節點
* visited[v] 代表樹的前序遍歷的次序
*/
//---------------連結串列結構------------
#define MAX_VEXNODE_NUM 20
typedef struct ArcNode{
int adjNode; //指向節點
struct ArcNode *nextArc; //下一條弧
}ArcNode;
typedef struct {
int data; //表頭資訊
ArcNode *firstArc; //第一條弧
} VNode[MAX_VEXNODE_NUM];
typedef struct AlGraph {
VNode vexs;
int vexnum, arcnum;
} ALGraph;
/**
* 建立連結串列
* @param graph
* @return
*/
Status createGraph(ALGraph &graph) {
cout << "please input the vexnum and arcnum" << endl;
cin >> graph.vexnum >> graph.arcnum;
cout<<"now input the nodes info"<<endl;
for(int i =0;i<graph.vexnum;i++){
cin>>graph.vexs[i].data;
graph.vexs[i].firstArc = NULL;
}
cout << "now input the arc info" << endl;
for (int i = 0; i < graph.arcnum; i++) {
int s, e;
cin >> s >> e;
ArcNode *s_next = new ArcNode;
*s_next = {e, graph.vexs[s].firstArc};
ArcNode *e_next = new ArcNode;
*e_next = {s, graph.vexs[e].firstArc};
graph.vexs[s].firstArc = s_next;
graph.vexs[e].firstArc = e_next;
}
}
//---------------求關鍵點演算法------------
int count = 0; //輔助求visisted
int visited[MAX_VEXNODE_NUM];
int low[MAX_VEXNODE_NUM];
void DFS(AlGraph G, int v) {
int min = visited[v] = ++count;
//遍歷
for (ArcNode *p = G.vexs[v].firstArc; p; p = p->nextArc) {
int w = p->adjNode;
if(!visited[w]){
DFS(G,w); //遞迴完後,會求出low[w]
if(low[w] < visited[v]){
min = low[w];
}else{ //low[w]>=visited[v]
cout<<G.vexs[v].data<<" ";
}
}else{ //如果已經遍歷過,說明w為v的祖先
if(visited[w] < min){
min = visited[w];
}
}
}
low[v] = min;
}
void getKeyPoint(AlGraph &graph){
//從0開始遍歷,把0作為根
count = 1; visited[0] = 1;
for(int i = 1;i<graph.vexnum;i++){
visited[i] = 0; //其餘節點沒有遍歷
}
//遍歷第一顆樹
ArcNode *p = graph.vexs[0].firstArc;
int v = p->adjNode;
DFS(graph,v);
if(count < graph.vexnum){
cout<<" "<<graph.vexs[0].data;
p = p->nextArc;
while(p){
DFS(graph,p->adjNode);
p = p->nextArc;
}
}
}
/**
* 輸入:
* n個點,e條邊
* n個點的資訊
* e行,每行兩個,i--j
* 輸入樣例:
* 7 7
* 0 1 2 3 4 5 6
* 0 2
* 1 2
* 2 3
* 2 4
* 3 5
* 4 5
* 5 6
* 輸出樣例:
* 5 2 2(為什麼多了個2,我也不知道,可能演算法原本就是這樣,搜尋了一些網上程式碼,似乎也會重複出來)
* @return
*/
int main(void) {
ALGraph graph;
createGraph(graph);
getKeyPoint(graph);
return 0;
}一定要理解那個公式再去寫程式,就變得豁然開朗了。
4. 有向無環圖及其應用
有向無環圖,簡稱為DAG圖,是一種描述工程或系統的進行過程的有效工具。幾乎所有工程都可分為若干個稱為活動的子工程,而這些子工程之間,通常受一定的約束,如其中某些自工程的開始在另一些子工程完成之後(拓撲排序)。另外,我們還關心一個問題,一個工程的完成最短需要多長時間?(關鍵路徑)
4.1 拓撲排序
拓撲排序常用於構建工程之間的先後關係:說個最通俗易懂的“工程”吧,在玩遊戲時,對角色的技能進行加點操作,我們能看到的技能點樹其實就是由拓撲排序生成的,某個技能的實現需要一定的前置技能。又如:大學課程有些課程一定是建立在某些先導課程的。如數字訊號處理需要訊號系統的知識,訊號系統需要高等數學知識等等。
常用的拓撲排序有兩種方式:
- 刪源法,依次刪除圖中入度為0的點,構成的序列就是拓撲排序。
- DFS逆棧法,其實在前文中求解有向圖的強連通分量時就使用了這個方法。
注意:拓撲不止一種排序結果。
還是來個例子說明一下:
那麼刪源法是如何操作的呢:
首先檢視圖中哪些點的入度為0?
顯然V1,V6入度為0,將兩點連通邊刪除後,得到:
現在刪去V3,V4。得到
所以整個拓撲排序為:V1,V6,V3,V4,V2,V5。
下面貼出兩種方式的具體程式碼
//
// Created by Raven on 2018/8/2.
//
#include "Public.h"
#include <stack>
#include <vector>
#include <algorithm>
/**
* 拓撲排序
* 有兩種方式可生成拓撲排序:
* 1.刪源法:依次刪除入度為0的節點
* 2.DFS棧反轉:根據DFS入棧,將出棧順序反轉即為拓撲排序
*/
//---------------方法一:刪源法------------
#define MAX_NODS_NUM 20
/**
* 使用連結串列來儲存
*/
typedef struct ArcNode {
int adjVertex; //弧指向節點
struct ArcNode *nextArc; //下一條弧
};
typedef struct VNode {
int data;
int indegree; //入度
struct ArcNode *firstArc;
};
typedef struct AlGraph {
VNode vertexs[MAX_NODS_NUM];
int vernum, arcnum;
};
/**
* 方法一:刪源法
* 設立零入度棧
* @param graph
* @return
*/
Status deleteOrigin(AlGraph graph) {
stack<int> s; //儲存零入度節點
for (int i = 0; i < graph.vernum; i++) {
if (!graph.vertexs[i].indegree) {
s.push(i);
}
}
int count = 0; //輔助變數,用於檢視是否能遍歷完
while (!s.empty()) {
int v = s.top();
s.pop();
cout << v << " ";
count++;
for (ArcNode *p = graph.vertexs[v].firstArc; p; p = p->nextArc) {
int w = p->adjVertex;
graph.vertexs[w].indegree--;
if (!graph.vertexs[w].indegree) {
s.push(w);
}
}
}
if (count < graph.vernum) {
return ERROR; //存在環
}
return OK;
}
/**
* dfs
* @return
*/
stack<int> sk; //dfs入棧順序
vector<int> vec; //出棧順序
bool visited[MAX_NODS_NUM];
Status dfs(AlGraph graph, int v) {
visited[v] = true;
sk.push(v);
for (ArcNode *p = graph.vertexs[v].firstArc; p; p = p->nextArc) {
int w = p->adjVertex;
if (!visited[w]) {
dfs(graph, w);
}
}
vec.push_back(sk.top());
sk.pop();
}
Status dfsTop(AlGraph graph) {
for (int i = 0; i < graph.vernum; i++) {
if (!visited[i]) {
dfs(graph, i);
}
}
}
Status createGraph(AlGraph &graph) {
cout << "please input the vnums and arcnum" << endl;
cin >> graph.vernum >> graph.arcnum;
//初始化表頭向量
for (int i = 0; i < graph.vernum; i++) {
graph.vertexs[i] = {i, 0, NULL};
}
cout << "please input the arc start and arc end" << endl;
for (int i = 0; i < graph.arcnum; i++) {
int s, e;
cin >> s >> e;
ArcNode *arc = new ArcNode;
// if (!arc) exit(ERROR);
*arc = {e, graph.vertexs[s].firstArc}; //構造邊
graph.vertexs[s].firstArc = arc;
graph.vertexs[e].indegree++; //增加入度
}
}
/**
* 輸入:
* n個節點,e條邊
* 接下來e行,i-> j
* 輸出拓撲排序:
*
* 輸入樣例:
* 6 8
* 0 1
* 0 3
* 0 2
* 2 1
* 2 4
* 3 4
* 5 3
* 5 4
* 輸出樣例:
* 5 0 3 2 1 4
* @return
*/
int main(void) {
//初始化連結串列
AlGraph graph;
createGraph(graph);
//方法一--刪源
deleteOrigin(graph);
cout << endl;
//方法二--dfs
dfsTop(graph);
reverse(vec.begin(), vec.end());
for (int v:vec) {
cout << v << " ";
}
return 0;
}4.2 關鍵路徑
什麼是關鍵路徑?關鍵路徑能什麼?
在網路中,路徑長度最長的那條路稱為關鍵路徑。關鍵能夠估算工程完成所需要花費的最短時間。以及如何對路徑中的某些活動(工程)進行優化能夠提升整個工程的速率。
關鍵路徑的求解使用到了拓撲排序,所以掌握了拓撲排序在加一點點動態規劃的思想,關鍵路徑的求解也不困難啦。
下面貼出具體程式碼,註釋得很詳細啦。
//
// Created by Raven on 2018/8/2.
//
#include <stack>
#include "Public.h"
/**
* 關鍵路徑
* 公式:
* e(i) = ve(i)
* l(i) = vl(k) - dut(<j,k>)
* k是i的後驅
* e代表弧(活動)的最早開始時間,l代表最晚開始時間
* ve代表邊(事件)的最早發生時間,vl代表最晚發生時間
* dut代表<j,k>耗時長
*
* ve(j) = Max{ve(i) + dut(<i,j>)} i為j的前驅 ,拓撲
* vl(i) = Min{vl(j) - dut(<i,j>)} ,逆拓撲
* 判定:
* e(i) == l(i) i為關鍵路徑上的關鍵活動
* ve(i) == vl(i) i為關鍵路徑上的關鍵事件
*/
//---------------實現------------
#define MAX_NODS_NUM 20
/**
* 使用連結串列來儲存
*/
typedef struct ArcNode {
int adjVertex; //弧指向節點
int weight; //權重,在這裡可作為活動時長
struct ArcNode *nextArc; //下一條弧
};
typedef struct VNode {
int data;
int indegree; //入度
struct ArcNode *firstArc;
};
typedef struct AlGraph {
VNode vertexs[MAX_NODS_NUM];
int vernum, arcnum;
};
//這裡採用刪源法求拓撲排序,當然dfs也可以
stack<int> rsk; //出棧順序即為逆拓撲排序
int ve[MAX_NODS_NUM];
int vl[MAX_NODS_NUM];
int e[MAX_NODS_NUM];
int l[MAX_NODS_NUM];
/**
* 求解拓撲排序,得到ve向量和逆拓撲排序棧
* @param graph
* @return
*/
Status deleteOrigin(AlGraph graph) {
stack<int> s; //儲存零入度節點
for (int i = 0; i < graph.vernum; i++) {
if (!graph.vertexs[i].indegree) {
s.push(i);
}
}
//初始化
for (int i = 0; i < graph.vernum; i++) {
ve[i] = 0;
}
int count = 0; //輔助變數,用於檢視是否能遍歷完
while (!s.empty()) {
int v = s.top();
s.pop();
rsk.push(v);
count++;
for (ArcNode *p = graph.vertexs[v].firstArc; p; p = p->nextArc) {
int w = p->adjVertex;
graph.vertexs[w].indegree--;
if (!graph.vertexs[w].indegree) {
s.push(w);
if (ve[w] < (ve[v] + p->weight)) {
ve[w] = ve[v] + p->weight;
}
}
}
}
if (count < graph.vernum) {
return ERROR; //存在環
}
return OK;
}
/**
* 關鍵路徑
* @param graph
* @return
*/
Status KeyPath(AlGraph graph) {
if (!deleteOrigin(graph)) return ERROR;
//初始化vl
for (int i = 0; i < graph.vernum; i++) {
vl[i] = ve[graph.vernum - 1];
}
//根據逆拓撲排序得到vl
while (!rsk.empty()) {
int v = rsk.top();
rsk.pop();
for (ArcNode *p = graph.vertexs[v].firstArc; p; p = p->nextArc) {
int w = p->adjVertex;
if (vl[v] > vl[w] - p->weight) {
vl[v] = vl[w] - p->weight;
}
}
}
//得到e和l
for (int i = 0; i < graph.vernum; i++) {
for (ArcNode *p = graph.vertexs[i].firstArc; p; p = p->nextArc) {
int k = p->adjVertex;
e[i] = ve[i];
l[i] = vl[k] - p->weight;
if (e[i] == l[i]) {
cout << i << "--" << k << endl;
}
}
}
}
Status createGraph(AlGraph &graph) {
cout << "please input the vnums and arcnum" << endl;
cin >> graph.vernum >> graph.arcnum;
//初始化表頭向量
for (int i = 0; i < graph.vernum; i++) {
graph.vertexs[i] = {i, 0, NULL};
}
cout << "please input the arc start and arc end" << endl;
for (int i = 0; i < graph.arcnum; i++) {
int s, e, w;
cin >> s >> e >> w;
ArcNode *arc = new ArcNode;
// if (!arc) exit(ERROR);
*arc = {e, w, graph.vertexs[s].firstArc}; //構造邊
graph.vertexs[s].firstArc = arc;
graph.vertexs[e].indegree++; //增加入度
}
}
/**
* * 輸入:
* n個節點,e條邊
* 接下來e行,i,j,w i-->j w為權重
* 輸出關鍵路徑:
*
* 輸入樣例:
* 6 8
* 0 1 3
* 0 2 2
* 1 3 2
* 1 4 3
* 2 3 4
* 2 5 3
* 3 5 2
* 4 5 1
* 輸出樣例:
* 0--2
* 2--3
* 3--5
* @return
*/
int main(void) {
AlGraph graph;
createGraph(graph);
//得到拓撲排序
KeyPath(graph);
return 0;
}
5. 最短路徑
這個應該沒啥說的了,寫程式碼都快寫吐了的兩個演算法。
5.1 某個源點到其餘個頂點–Dijkstra
//
// Created by Raven on 2018/8/2.
//
#include <algorithm>
#include "Public.h"
/**
* Dijkstra演算法
* 從某個源點到其餘各定點的最短路徑
*/
#define INF 10000
const int N = 6;
int D[][N] = {
{0, 6, 1, 5, INF, INF},
{6, 0, 5, INF, 3, INF},
{1, 5, 0, 5, 6, 4},
{5, INF, 5, 0, INF, 2},
{INF, 3, 6, INF, 0, 6},
{INF, INF, 4, 2, 6, 0}
};
bool allVisited(bool visited[N]) {
for (int i = 0; i < N; i++) {
if (!visited[i]) {
return false;
}
}
return true;
}
int chooseMin(int cost[N], bool visited[N]) {
int min = INF;
int ind = -1;
for (int i = 0; i < N; i++) {
if (!visited[i] && min >= cost[i]) {
ind = i;
min = cost[i];
}
}
return ind;
}
/**
* D演算法,求v到其餘各點的最短路徑長
* @param D
* @param v
* @return
*/
Status Dijkstra(int D[][N], int v) {
int cost[N];
int pathTree[N];
//初始化一些引數
bool visited[N];
for (int i = 0; i < N; i++) {
cost[i] = D[v][i];
visited[i] = false;
pathTree[i] = i;
}
int cur = v;
visited[v] = true;
while (!allVisited(visited)) {
for (int i = 0; i < N; i++) {
if (!visited[i]) {
if (cost[i] > D[v][cur] + D[cur][i]) {
cost[i] = D[v][cur] + D[cur][i];
pathTree[i] = cur;
}
}
}
//選擇最小的
cur = chooseMin(cost, visited);
visited[cur] = true;
}
//輸出
for (int i = 0; i < N; i++) {
if (cost[i] != INF) {
cout << v << "-->" << i << " len:" << cost[i] << " path:";
int p = i;
char c[2]; //不知道C語言這字串怎麼拼接才對,可能處理得比較蹩腳。(用慣java,感覺還是java的字串好用多了)
sprintf(c, "%d", p);
string path(c);
while (p != pathTree[p]) {
p = pathTree[p];
sprintf(c, "%d", p);
path = path + ">--" + c;
}
sprintf(c, "%d", v);
path = path + ">--" + c;
reverse(path.begin(), path.end());
cout << path << endl;
} else if (i != v) {
cout << v << " can't go to " << i << endl;
}
}
}
int main(void) {
Dijkstra(D, 0);
return 0;
}5.2 每一對頂點之間的最短路徑–Floyd
//
// Created by Raven on 2018/8/2.
//
#include "Public.h"
/**
* Floyd 演算法
* 每一對頂點之間的最短路徑
* 演算法主要內容:
* 存在兩個矩陣:D和P陣
* D:存放最短徑長
* P:存放<i,j>之間的中轉
*/
#define INF 10000
const int N = 6;
int G[][N] = {
{0, 6, 1, 5, INF, INF},
{6, 0, 5, INF, 3, INF},
{1, 5, 0, 5, 6, 4},
{5, INF, 5, 0, INF, 2},
{INF, 3, 6, INF, 0, 6},
{INF, INF, 4, 2, 6, 0}
};
int main(void) {
int D[N][N], P[N][N];
//初始化
for (int i = 0; i < N; ++i) {
for (int j = 0; j < N; ++j) {
D[i][j] = G[i][j];
if (D[i][j] != INF) {
P[i][j] = j;
}
}
}
//FLoyd
for (int k = 0; k < N; k++) {
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
if (D[i][j] > D[i][k] + D[k][j]) {
D[i][j] = D[i][k] + D[k][j];
P[i][j] = P[i][k];
}
}
}
}
//輸出
int v;
cout << "please input which node you wanna to know" << endl;
cin >> v;
for (int i = 0; i < N; i++) {
if (D[v][i] != INF) {
cout << v << "--" << i << " len:" << D[v][i] << " path:";
cout << v;
int p = P[v][i];
相關推薦
資料結構實驗六是否同一顆二叉樹
資料結構與演算法實驗報告
第六次實驗
姓名:孫瑞霜
一、實驗目的
1、熟練掌握學習的每種結構及其相應演算法;
2、理論聯絡實際,會對現實問題建模並設計相應演算法。
3、優化演算法,使得演算法效率適當提高
二、實驗要求:
1. 認真閱讀和掌握教材上和本實驗相關的內
資料結構(六)-圖(二)--演算法篇
圖-常用演算法
4. 圖的連通性問題
在無向圖中,如果無向圖是連通圖,僅需從任意一點出發,進行深度優先搜尋或廣度優先搜尋,邊可訪問到圖中所有頂點。對非連通圖,則多個頂點出發進行搜尋,而每一次從一個新的起始點出發進行搜尋過程中得到的頂點訪問序列恰為
考研資料結構複習之線性表(二)
單鏈表的學習
#pragma once
typedef char DataType;
class SSeqListTest
{
public:
SSeqListTest();
~SSeqListTest();
};
typedef struct Node {
資料結構實驗之棧與佇列二:一般算術表示式轉換成字尾式(SDUT 2132)
題目連結
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int ok(char ch, char sh)
{
if(sh == '(')return 1;
if((ch ==
浙大版《資料結構》習題4.3 是否二叉搜尋樹 (25 分)
本題要求實現函式,判斷給定二叉樹是否二叉搜尋樹。
函式介面定義:
bool IsBST ( BinTree T );
其中BinTree結構定義如下:
typedef struct TNode *Position;
typedef Position BinT
資料結構實驗之查詢一:二叉排序樹 (SDUT 3373)
二叉排序樹(Binary Sort Tree),又稱二叉查詢樹(Binary Search Tree),也稱二叉搜尋樹。
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
struct nod
資料結構-高精度大整數(二)
接著上一篇文章的內容,這次來實現加減乘除演算法。
先來回顧一下上次學過的內容,給出大數類的儲存定義:
struct BigInteger
{
friend BigInteger operator - (BigInteger, BigInteger);
fr
資料結構作業19—靜態查詢表與二叉排序樹(選擇題)
2-1將{ 5, 11, 13, 1, 3, 6 }依次插入初始為空的二叉搜尋樹。則該樹的後序遍歷結果是:(3分)
A.1, 3, 11, 6, 13, 5
B.1, 3, 5, 6, 13, 11
C.3, 1, 6, 13, 11, 5
D.3, 1
《 常見演算法與資料結構》符號表ST(4)——二叉查詢樹刪除 (附動畫)
符號表ST(4)——二叉查詢樹刪除 (附動畫)
本系列文章主要介紹常用的演算法和資料結構的知識,記錄的是《Algorithms I/II》課程的內容,採用的是“演算法(第4版)”這本紅寶書作為
資料結構中常見的樹(BST二叉搜尋樹、AVL平衡二叉樹、RBT紅黑樹、B-樹、B+樹、B*樹)
BST樹
即二叉搜尋樹:
1.所有非葉子結點至多擁有兩個兒子(Left和Right);
2.所有結點儲存一個關鍵字;
3.非葉子結點的左指標指向小於其關鍵字的子樹,右指標指向大於其關鍵字的子樹;
如:
資料結構之---C語言實現平衡二叉樹(AVL樹)
//AVL(自動平衡二叉樹)
#include <stdio.h>
#include <stdlib.h>
typedef int ElemType;
//每個結點的平均值
typedef enum
{
EH = 0,
LH =
資料結構實驗9:圖的相關操作(待填坑)
實驗9
姓名: 學號:班級:
8.1 實驗目的
(1) 掌握圖的基本概念。
(2) 掌握圖的儲存結構的設計與實現,基本運算的實現。
(3) 熟練掌握圖的兩種遍歷演算法、遍歷生成樹及遍歷演算法的應用。
8.2 實驗任務
分別設計圖(網)的鄰接矩陣、鄰接表儲存結構,編寫演算法實
【資料結構樹表的查詢】二叉排序樹詳解和程式碼(生成、插入、查詢、最大值、最小值、刪除、中序遍歷、銷燬)
二叉排序樹(簡稱BST)又稱二叉查詢(搜尋)樹,其定義為:二叉排序樹或者是空樹,或者是滿足如下性質的二叉樹:
(1)若它的左子樹非空,則左子樹上所有記錄的值均小於根記錄的值;
(2)若它的右子樹非空,則右子樹上所有記錄的值均大於根記錄的值;
JAVA資料結構--根據樹高生成完全二叉樹(java實現)
public class BTree {
private int node;
private BTree LChild ;
private BTree RChild ;
private BTree(int node){
this.node = nod
Redis資料結構詳解之List(二)
Redis中關於List列表的命令詳解
1、redis中list列表的資料插入命令:lpush,rpush,linsert
127.0.0.1:6379>rpush mylist 1 ---結果為:(integer) 1
127.0.0.1:6379&g
資料結構-----Binary Tree Inorder Traversal (二叉樹的中序遍歷)
Binary Tree Inorder Traversal (二叉樹的中序遍歷)
題目描述:
Given a binary tree, return the inorder traversal of its nodes' values.
For example:
Giv
資料結構之紅黑樹(二)——插入操作
插入或刪除操作,都有可能改變紅黑樹的平衡性,利用顏色變化與旋轉這兩大法寶就可應對所有情況,將不平衡的紅黑樹變為平衡的紅黑樹。
在進行顏色變化或旋轉的時候,往往要涉及祖孫三代節點:X表示操作的基準節點,P代表X的父節點,G代表X的父節點的父節點。
我們先來大體預覽一下插入的
資訊學奧賽一本通(C++版) 第三部分 資料結構 第四章 圖論演算法
資訊學奧賽一本通(C++版) 第三部分 資料結構 第四章 圖論演算法
http://ybt.ssoier.cn:8088/
第一節 圖的遍歷
//1341 【例題】一筆畫問題
//在想,是輸出尤拉路,還是歐拉回路
//從哪點開始遍歷,
//點的資料範圍,邊的資料範圍
2015年大二上-資料結構-陣列與廣義表(2)-4.下三角矩陣的壓縮儲存及基本運算
/*
*Copyright (c) 2014,煙臺大學計算機學院
*All rights reserved.
*檔名稱:Annpion.cpp
*作者:王耀鵬
*完成日期:2015年12月16日
*版本號:v1.0
*
*問題描述:下三角矩陣的壓縮儲存及基本運算
*輸入描述
2015年大二上-資料結構-陣列與廣義表(2)-3.上三角矩陣的壓縮儲存及基本運算
/*
*Copyright (c) 2014,煙臺大學計算機學院
*All rights reserved.
*檔名稱:Annpion.cpp
*作者:王耀鵬
*完成日期:2015年12月16日
*版本號:v1.0
*
*問題描述:上三角矩陣的壓縮儲存及基本運算
*輸入描述