資訊學奧賽一本通(C++版) 第三部分 資料結構 第四章 圖論演算法
資訊學奧賽一本通(C++版) 第三部分 資料結構 第四章 圖論演算法
http://ybt.ssoier.cn:8088/
第一節 圖的遍歷
//1341 【例題】一筆畫問題
//在想,是輸出尤拉路,還是歐拉回路
//從哪點開始遍歷,
//點的資料範圍,邊的資料範圍
//尤拉路的理解,經過所有點,歐拉回路的理解,某點出發,最後回到某點,中間經過其他所有的點
//一直很困後,尤拉路,還是歐拉回路,突然想到在尤拉路里加一層判斷,進一步判斷是否有歐拉回路
//從資料輸出來看,該題是個無向圖,準備用鄰接矩陣來儲存資料
//提交,兩個結果,不是答案錯誤,就是執行超時
//歐拉回路
//看了此文,深受啟發https://www.cnblogs.com/sssy/p/6682871.html?utm_source=itdadao&utm_medium=referral
//大幅修改程式碼
//提交,沒有超時了,不過,全是答案錯誤,
//參考http://www.cnblogs.com/zhourongqing/archive/2012/09/18/2690185.html 提供一組測試資料
//輸入:
//6 9
//1 2
//2 3
//3 4
//4 2
//4 5
//2 5
//5 6
//4 6
//輸出:
//5 6 4 5 2 4 3 2 1
//明白了,自己對尤拉路或迴路的誤解,並不是每個點只通過一次,而是每條邊最多通過一次,將所有點都遍歷了,
//具體到每個點,可以通過多次,那麼該題的核心是對邊的處理
//參考了https://wenku.baidu.com/view/f533dc147c1cfad6185fa7bb.html寫法 除錯程式過程中,發現該寫法是錯誤的
//程式繼續大改,樣例繼續通過,提交AC 2017-11-11 22:46
//尤拉演算法與回溯演算法很不同。
//成熟的方法 2017-11-13 18:48
#include <stdio.h>
#include <string.h>
int a[510][510],b[1100],du[510],n,cnt=0;//b存路徑
void dfs(int i){
int j;
for(j=1;j<=n;j++)
if(a[i][j]){
a[i][j]=0,a[j][i]=0;
dfs(j);
}
b[cnt++]=i;
}
int main(){
int m,i,j,u,v,count=0,start;
memset(a,0,sizeof(a)),memset(du,0,sizeof(du));
scanf("%d%d",&n,&m);
for(i=1;i<=m;i++){
scanf("%d%d",&u,&v);
a[u][v]=1,a[v][u]=1,du[u]++,du[v]++;
}
start=1;//起點,歐拉回路
for(i=1;i<=n;i++)
if(du[i]%2==1){
count++;
if(count==1)
start=i;//尤拉路徑
}
dfs(start);
for(i=cnt-1;i>=0;i--)printf("%d ",b[i]);
return 0;
}
不成熟的方法:
#include <stdio.h>
#include <string.h>
int a[1000][1000],n,m,d[1000],b[1000],count=0;
void dfs(int i){//尤拉路
int j;
for(j=1;j<=n;j++){
if(a[i][j]==1){
a[i][j]=0,a[j][i]=0;
dfs(j);
b[count++]=j;
}
}
}
int main(){
int i,j,u,v,cnt=0;
memset(a,0,sizeof(a));
memset(d,0,sizeof(d));
scanf("%d%d",&n,&m);
for(i=1;i<=m;i++){//此處寫成 for(i=1;i<=n;i++)大失水準
scanf("%d%d",&u,&v);
a[u][v]=1,a[v][u]=1;
d[u]++,d[v]++;
}
u=1;
for(i=1;i<=n;i++)
if(d[i]%2==1){
cnt++;
if(cnt==1)
u=i;
}
dfs(u);
for(i=0;i<count;i++)
printf("%d ",b[i]);
printf("%d",u);
return 0;
}
//1374 鏟雪車(snow)
//看完題目後,明顯感覺題目的樣例輸出部分有問題
//搜尋網路,https://www.cnblogs.com/olahiuj/p/5781343.html給出詳細輸入輸出資料,經確認與該題不符
//繼續搜尋,http://www.oier.cc/ssoj2426%E9%93%B2%E9%9B%AA%E8%BD%A6%E9%97%AE%E9%A2%98/樣例與該題相符 ,摘抄如下
//輸入:
//0 0
//0 0 10000 10000
//5000 -10000 5000 10000
//5000 10000 10000 10000
//輸出:
//3:55
//思路也摘抄如下:
//每一條路都只剷雪一遍,這樣是最節省時間的;因為是雙向道路,
//所以可以從任何一個點走一圈回到起點,這就是歐拉回路。知道路程和速度,
//就可以快速求出時間,輸出時注意時間的格式以及精確到分鐘需要四捨五入就行。
//(平方可能會超過int,建議使用long long)
//不得不承認,上述在該題寫的程式碼相當棒,美中不足就是程式碼是圖片版本的。
//本人對該題看法:
//該題,沒說明那些道路有雪,那些道路無雪,從解題的情況來看,是每個道路都有雪,並且是兩個車道都有雪
//AC 2017-11-12 9:26
#include <stdio.h>
#include <math.h>
int main(){
long long s,e,x1,y1,x2,y2,h,m;
double d=0,ans;
scanf("%lld%lld",&s,&e);//這句只是為了讀取,在題中資料無用,因是歐拉回路,故算總路程,哪點出發都行
while(scanf("%lld%lld%lld%lld",&x1,&y1,&x2,&y2)!=EOF)
d+=sqrt((x2-x1)*(x2-x1)+(y2-y1)*(y2-y1));//此處寫成d=sqrt((x2-x1)*(x2-x1)+(y2-y1)*(y2-y1));//若用int 該題資料會溢位
ans=d*2/1000/20;//此處寫成ans=d/1000/20;//2兩倍距離1000化成km,20對應小時
h=(long long)ans;
m=(long long)((ans-h)*60+0.5);//0.5四捨五入
printf("%lld:%02lld",h,m);//還要注意時間的輸出格式,注意補零 ,該題要做對很不容易
return 0;
}
//洛谷 P2731 騎馬修柵欄 Riding the Fences
//1375 騎馬修柵欄(fence)
//開始以為柵欄對應點,以為該題是哈密爾頓迴路,整道題讀完,發現柵欄對應邊,該題是尤拉路徑
//該題難點,總的點的個數沒有說明,看了一眼https://www.cnblogs.com/gzhonghui/p/5707943.html程式碼
//需區分尤拉路徑,歐拉回路
//樣例通過,提交,測試點6,7,8答案錯誤
//重新看了一遍https://www.cnblogs.com/gzhonghui/p/5707943.html程式碼,發現最小的點竟然可能不是1,也得自個求
//修改,提交,測試點6,7,8答案錯誤
//搜尋網路,https://www.luogu.org/wiki/show?name=%E9%A2%98%E8%A7%A3+P2731
//提到,兩頂點間可能有多個柵欄,於是我們就要統計2個點之間的柵欄條數(好坑啊)
//馬上修改,提交,還是錯了測試點6,7,8
//下載測試點6的資料,才發現,問題是意識到了,但讀取資料的時候沒有做邊的自增修改,
//修改,提交,發現錯了測試點7,8
//繼續下載測試點7的資料,
//仿照他人程式碼就行修改,提交AC 2017-11-12 19:14
//一個疑問,記錄路徑時,放在dfs()之前,與放在迴圈結束之後,為什麼會有偏差,函待解決。
#include <stdio.h>
#include <string.h>
int a[510][510],b[2000],begin=999999,n=0,du[510],cnt_b=0;//b[]記錄走過的點,注意點可以重複,注意b要開得大些 n點的數目
int max(int a,int b){
return a>b?a:b;
}
int min(int a,int b){
return a<b?a:b;
}
void dfs(int i){
int j;
for(j=begin;j<=n;j++)//此處寫成 for(j=1;j<=n;j++)
if(a[i][j]){
a[i][j]--,a[j][i]--;//此處寫成 a[i][j]=0,a[j][i]=0;
//b[cnt_b++]=j;//為了解決測試點7,8
dfs(j);
}
b[cnt_b++]=i;//為了解決測試點7,8
}
int main(){
int m,i,j,u,v,cnt_du=0,start;
memset(a,0,sizeof(a)),memset(du,0,sizeof(du));
scanf("%d",&m);
for(i=1;i<=m;i++){
scanf("%d%d",&u,&v);//無向圖
a[u][v]++,a[v][u]++,du[u]++,du[v]++;//此處寫成 a[u][v]=1,a[v][u]=1,du[u]++,du[v]++;
n=max(n,max(u,v)); //參考他人程式碼,才想到的
begin=min(begin,min(u,v));
}
start=begin;//此處寫成start=1;//歐拉回路,從第1個點開始
for(i=begin;i<=n;i++)//此處寫成 for(i=1;i<=n;i++)
if(du[i]%2==1){
cnt_du++;
if(cnt_du==1)start=i;//尤拉路徑,從第i個點開始
}
dfs(start);
//printf("%d\n",start);//為了解決測試點7,8
//for(i=0;i<cnt_b;i++)printf("%d\n",b[i]);//為了解決測試點7,8
for(i=cnt_b-1;i>=0;i--)printf("%d\n",b[i]);//為了解決測試點7,8
return 0;
}
2017-11-12 20:50 AC該節內容
第二節 最短路徑演算法
//1342 【例4-1】最短路徑問題
//因n<=100,可以考慮Floyd演算法
//樣例很快通過,提交AC 2017-11-12 23:01
#include <stdio.h>
#include <math.h>
#define INF 1999999999
double d[110][110];
long long x[110],y[110];
int main(){
int n,m,i,j,k,u,v;
double s;
scanf("%d",&n);
for(i=1;i<=n;i++)scanf("%lld%lld",&x[i],&y[i]);
scanf("%d",&m);
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
d[i][j]=d[j][i]=INF;
for(i=1;i<=n;i++)d[i][i]=0;
for(i=1;i<=m;i++){
scanf("%d%d",&u,&v);
s=sqrt((x[u]-x[v])*(x[u]-x[v])+(y[u]-y[v])*(y[u]-y[v]));
d[u][v]=s,d[v][u]=s;//無向圖
}
for(k=1;k<=n;k++)//以某個點為中轉,整個鄰接邊重新算一遍,故k打頭
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(d[i][j]>d[i][k]+d[k][j])
d[i][j]=d[i][k]+d[k][j];
scanf("%d%d",&u,&v);
printf("%.2lf",d[u][v]);
return 0;
}
//1342 【例4-1】最短路徑問題
//n<=100 考慮用Floyd演算法,簡單,方便,快捷
//樣例通過,提交AC 2017-11-27
#include <stdio.h>
#include <math.h>
#define INF 999999999
struct node{
int x,y;
}p[110];
double a[110][110],d;
int main(){
int i,j,k,n,m,u,v,x1,y1,x2,y2,s,t;
scanf("%d",&n);
for(i=1;i<=n;i++)scanf("%d%d",&p[i].x,&p[i].y);
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(i==j)a[i][j]=0;
else a[i][j]=INF;
scanf("%d",&m);
for(i=1;i<=m;i++){
scanf("%d%d",&u,&v);
x1=p[u].x,y1=p[u].y,x2=p[v].x,y2=p[v].y;
d=sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
a[u][v]=d,a[v][u]=d;//無向圖
}
scanf("%d%d",&s,&t);
for(k=1;k<=n;k++)
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(a[i][j]>a[i][k]+a[k][j])
a[i][j]=a[i][k]+a[k][j];
printf("%.2lf",a[s][t]);
return 0;
}
//1343 【例4-2】牛的旅行
//P1522 牛的旅行 Cow Tours
http://blog.csdn.net/mrcrack/article/details/70112975
//首先說明一點,翻譯得很不好,還是看原版的比較好。
//http://blog.csdn.net/supersnow0622/article/details/9763979此文寫得不錯,摘抄如下:
//分析:首先要連在一起修路的這兩個牧區,之前是不連通的。其次就是這兩個牧區修路之後,
//相隔最遠的兩個牧區的距離最小。其實,只要列舉任意不連通的兩個牧區在計算這種情況下的最遠的距離就好了,
//然後在這些最遠的距離中找到距離最小(題目要求半徑最小)的一個就是所求了。
//關鍵是在兩個不連通的牧區修路之後求牧場的半徑呢?假設已將one牧區種的D和two牧區中的F相連,
//想一下,這個牧場的半徑是不是等於與D相距最遠的點到D的距離+D與F的距離+與F相距最遠的點的距離呢?
//這樣的求法是滿足題目所說的牧場的半徑是相距最遠的兩個點的距離。
//所以思路很快就出來了:
//1.用floyed計算任意兩點間的距離
//2.計算每個點與其他點的最遠距離
//3.計算任意兩個不連通的點修路之後牧場的半徑。
//http://www.xuebuyuan.com/1457314.html此文給出了英文原版題目,讀下來,配合中文意思,弄懂題目了。
//http://www.nocow.cn/index.php/USACO/cowtour根據該文,弄懂了,為什麼
//那我們只需要計算新連成的區塊的直徑,然後與原來的所有區塊的直徑放在一起,取最大直徑就可以了
//突然對為什麼取最大直徑,又心存疑慮,想了3個小時,想不通,暫時擱置吧。
//老外的題,與中國的題,確實存在著文化差異。感嘆。
//編碼的過程中,真是服了,洛谷的樣例輸入資料有問題。查找了一通,發現沒有問題,資料格式本就是如此。折騰了一場。
#include <stdio.h>
#include <string.h>
#include <math.h>//洛谷中,該標頭檔案,必須以C++形式提交。
#define INF 1000000
int x[150+10],y[150+10];
double a[150+10][150+10],d[150+10],minD=INF;
char s[200];
double dis(int x1,int y1,int x2,int y2){
return sqrt((double)(x1-x2)*(x1-x2)+(double)(y1-y2)*(y1-y2));//別忘了強轉,否者容易溢位100000*100000
}
int main(){
int i,j,k,n,w;
memset(d,0,sizeof(d));
scanf("%d",&n);
for(i=1;i<=n;i++)
scanf("%d%d",&x[i],&y[i]);
for(i=1;i<=n;i++){
scanf("%s",s+1);
for(j=1;j<=n;j++){
if(i!=j){
if(s[j]=='0')
a[i][j]=a[i][j]=INF;
else{
a[i][j]=a[j][i]=dis(x[i],y[i],x[j],y[j]);
}
}else
a[i][j]=0;
}
}
for(k=1;k<=n;k++)//floyd演算法
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(a[i][j]>a[i][k]+a[k][j])
a[i][j]=a[i][k]+a[k][j];
for(i=1;i<=n;i++)//連通區塊裡找最大值
for(j=1;j<=n;j++)
if(a[i][j]<INF&&a[i][j]>d[i])
d[i]=a[i][j];
for(i=1;i<=n;i++)//連線兩個牧區,找最小值。
for(j=1;j<=n;j++)
if(a[i][j]==INF&&minD>d[i]+d[j]+dis(x[i],y[i],x[j],y[j]))
minD=d[i]+d[j]+dis(x[i],y[i],x[j],y[j]);
for(i=1;i<=n;i++)//此處想不明白,為什麼找最大值。 等水平高了再回看此題。2017-6-20 21:23
if(minD<d[i])
minD=d[i];
printf("%.6lf\n",minD);//1此處寫成printf("%d\n",minD);低階錯誤
return 0;
}
//1344 【例4-4】最小花費
//從題目構成看,是求最短路徑
//1<=n<=2000 Floyd演算法用不了,上Dijkstra演算法
//因資料範圍限制,不採用鄰接矩陣,採用鄰接表的方式儲存圖資料
//但轉念一想,該題沒給邊的資料範圍,故還是採用鄰接矩陣進行儲存
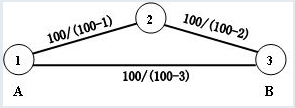
//在測試樣例的過程中,發現 樣例 輸入 輸出竟然 沒弄懂。
//1->3 3 100/(1-0.03)=103.09278350515463917525773195876
//1->2 2->3 100/((1-0.01)(1-0.02))= 103.09278350515463917525773195876
//寫到此刻,意識到,該題挺難的。
//暫時擱置2017-11-27
//http://blog.sina.com.cn/s/blog_4f3b79d00100aqi7.html此文介紹得不錯
//【試題解析】
//本題其實是求從A到B的最短路徑問題(可用Dijstra或SPFA演算法),解題的關鍵是構圖:
//以人員編號為頂點,若x號人和y號人之間可以相互轉賬則在x和y之間連一條邊,邊的權為100/(100-z)。對於樣例構圖如下:
//最小花費——一道最短路徑試題
//因為B到帳後收到100元,所以,原題等價於求從B到A的最短路徑(權值相乘),由於乘法滿足交換律,故也可求從A到B的最短路徑。對於樣例,從A到B的最短路徑為:1→2→3,權值為:[100/(100-1)]*[100/(100-2)]= 1.0307153164,最後的結果為:103. 07153164(保留小數點後8位)。
//演算法是與一般的最短路徑不同,
//樣例通過,提交,測試點,答案全部錯誤,一查,漏了二維陣列的初始化,新增,提交AC, 2017-12-1
#include <stdio.h>
#include <string.h>
#define INF 999999999
int n,m,vis[2010],A,B;
double d[2010],a[2010][2010];
int findMin(){
int i,k;
double min=999999999;
for(i=1;i<=n;i++)
if(vis[i]==0&&d[i]<min)
min=d[i],k=i;
return k;
}
void Dijkstra(){//剩下n-1個點
int cnt=1,k,i;
while(cnt<n){//此處寫成 cnt<n 花了點時間
cnt++;
k=findMin();
vis[k]=1;
for(i=1;i<=n;i++)
if(vis[i]==0&&d[i]>d[k]*a[k][i])//以k為中轉
d[i]=d[k]*a[k][i];
}
}
int main(){
int i,j,u,v,w;
memset(a,0,sizeof(a));memset(vis,0,sizeof(vis));
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++)//漏了初始化,提交答案全部錯誤
for(j=1;j<=n;j++)
if(i==j)a[i][j]=0;
else a[i][j]=INF;
for(i=1;i<=m;i++)scanf("%d%d%d",&u,&v,&w),a[u][v]=a[v][u]=100.0/(100-w);//此處不能寫成a[u][v]=a[v][u]=100.0*100/(100-w);仔細想過,確實錯的//無向圖
scanf("%d%d",&A,&B);
vis[A]=1;
for(i=1;i<=n;i++)
if(a[A][i])
d[i]=a[A][i];
Dijkstra();
printf("%.8lf",d[B]*100);
return 0;
}
//1345 【例4-6】香甜的黃油
//若用Floyd演算法,該題很快能解決,無奈牧場數P(2≤P≤800)超時是必然
//準備採用SPFA演算法,但對超時還是有顧忌,演算法複雜度 N*P*C
//準備翻看他人程式碼,但轉念一想,還是要驗證自己的思路
//先自個編。
//翻看了http://blog.csdn.net/loi_imcy/article/details/49405447
//https://www.cnblogs.com/zbtrs/p/5947209.html
//兩篇文章,發現,想是想到了,就欠缺一步編碼,可惜了。
//樣例通過,提交AC 2017-12-24 16:49
//翻看 https://www.luogu.org/problemnew/solution/P1828
//SPFA演算法,O(kE) E是邊數,k是常數,平均值為2。Bellman-Ford演算法的一種佇列實現
//該題,演算法複雜度O(k*E*p)
#include <stdio.h>
#include <string.h>
#define INF 999999999
int n,p,c,head[810],cnt=0,d[810],q[10*810],vis[810],a[510];
struct node{
int to,next,w;
}e[1500*2];//無向圖
void SPFA(int s){
int u,v,b,h,t,i,w;
memset(vis,0,sizeof(vis));
for(i=1;i<=p;i++)d[i]=INF;
d[s]=0,h=t=1,q[t]=s,t++,vis[s]=1;
while(h<t){
u=q[h];
for(b=head[u];b;b=e[b].next){
v=e[b].to,w=e[b].w;
if(d[v]>d[u]+w){
d[v]=d[u]+w;
if(vis[v]==0)q[t]=v,t++,vis[v]=1;
}
}
vis[u]=0;
h++;
}
}
void add_edge(int u,int v,int w){
cnt++,e[cnt].to=v,e[cnt].w=w,e[cnt].next=head[u],head[u]=cnt;
}
int main(){
int i,j,u,v,w,ans=INF,sum;
memset(head,0,sizeof(head));
scanf("%d%d%d",&n,&p,&c);
for(i=1;i<=n;i++)scanf("%d",&a[i]);
for(i=1;i<=c;i++){
scanf("%d%d%d",&u,&v,&w);
add_edge(u,v,w),add_edge(v,u,w);
}
for(i=1;i<=p;i++){
SPFA(i),sum=0;
for(j=1;j<=n;j++)sum+=d[a[j]];
ans=ans>sum?sum:ans;
}
printf("%d",ans);
return 0;
}
//1376 信使(msner)
//1<=n<=100採用floyd演算法,簡單,易寫
//在最短路徑中找最大值,既為最短時間,請注意,起點是指揮所1,終點是剩下的n-1個點
//樣例通過,提交AC 2017-11-30
#include <stdio.h>
#define INF 999999999
int a[110][110];
int main(){
int i,j,k,n,m,max=-999999999,u,v,w;
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(i==j)a[i][j]=0;
else a[i][j]=INF;
for(i=1;i<=m;i++){
scanf("%d%d%d",&u,&v,&w);
a[u][v]=w,a[v][u]=w;//無向圖
}
for(k=1;k<=n;k++)
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(a[i][j]>a[i][k]+a[k][j])
a[i][j]=a[i][k]+a[k][j];
for(j=1;j<=n;j++)
if(a[1][j]>max)max=a[1][j];
if(max==INF)printf("-1");
else printf("%d",max);
return 0;
}
//1377 最優乘車(travel)
//懷疑該題的輸入資料有誤
//翻看http://codevs.cn/problem/1722/發現是同一道題
//輸入資料如下:
//3 7
//6 7
//4 7 3 6
//2 1 3 5
//http://blog.csdn.net/u011434547/article/details/37925685通過此文基本弄明白了資料的讀取以及處理
//思路摘抄如下:
//主要的還是對資料的處理,一個巴士線路上的站都只要乘一次就到了,那麼我們建立圖,
//如果i站點和j站點同時出現在一個巴士線路上就連一條邊,他們之間的權值為1.
//然後用最短路處理,dijkstra和floyed都能處理
//為了方便讀取,採用C++方式編寫
//樣例通過,提交,測試點1-3,6-8,10答案錯誤
//scanf("%d%d\n",&m,&n);//請注意此處寫法,scanf("%d%d\n",&m,&n);原來寫成 scanf("%d%d",&m,&n);getchar();測試點1-3,6-8,10答案錯誤
//提交AC 2017-12-24 21:46 該題很大一部分難在資料讀取。
//該題是有向圖
#include <iostream>
#include <sstream>
#include <string>
#include <cstdio>
using namespace std;
#define INF 999999999//此處寫成 999999999
int num[510],a[510][510];
int main(){
int m,n,i,j,k,len,x;
string str;
scanf("%d%d\n",&m,&n);//請注意此處寫法,scanf("%d%d\n",&m,&n);原來寫成 scanf("%d%d",&m,&n);getchar();測試點1-3,6-8,10答案錯誤
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(i==j)a[i][j]=0;
else a[i][j]=INF;
for(k=1;k<=m;k++){//以下讀取手法,請注意學習
getline(cin,str);
stringstream in(str);
len=0;
while(in>>x)num[++len]=x;
for(i=1;i<=len;i++)
for(j=i+1;j<=len;j++)
a[num[i]][num[j]]=1;
}
for(k=1;k<=n;k++)//此處寫成 for(k=1;k<=n;k++)
for(i=1;i<=n;i++)//此處寫成for(i=1;i<=n;i++)
for(j=1;j<=n;j++)//此處寫成 for(j=1;j<=n;j++)
if(a[i][j]>a[i][k]+a[k][j])
a[i][j]=a[i][k]+a[k][j];
if(a[1][n]==INF)printf("NO");//此處寫成 if(a[1][n]==INF)
else printf("%d",a[1][n]-1);//此處寫成 else printf("%d",a[1][n]-1);
return 0;
}
//1378 最短路徑(shopth)
//n<=80採用Floyd演算法
//該題,資料讀取遇到了極大的障礙
//翻看http://www.oier.cc/ssoj2433%e6%9c%80%e7%9f%ad%e8%b7%af%e5%be%84shopth/程式碼,讀取資料受到啟發
//樣例通過,提交AC,Floyd演算法真牛,能處理負邊。2017-12-13
#include <stdio.h>
#define INF 999999999
int a[100][100];
int main(){
int n,s,i,j,b,k;
scanf("%d%d",&n,&s);
for(i=1;i<=n;i++){
for(j=1;j<=n;j++){
if(scanf("%d",&b)==1)a[i][j]=b;//資料讀取技巧
else a[i][j]=INF;
}
}
for(k=1;k<=n;k++)
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(a[i][j]>a[i][k]+a[k][j])a[i][j]=a[i][k]+a[k][j];
for(j=1;j<=n;j++)
if(j!=s)printf("(%d -> %d) = %d\n",s,j,a[s][j]);
return 0;
}
//1379 熱浪(heatwv)
1.//P1339 [USACO09OCT]熱浪Heat Wave
http://blog.csdn.net/mrcrack/article/details/70112975
//無向圖
//鄰接矩陣2500*2500佔空間有點多,準備嘗試鄰接表
//Dijkstra 鄰接表的寫法,這篇文章寫得不錯 https://www.douban.com/note/296102336/
//很快編寫好,樣例通過,提交AC,一次性成功,程式碼寫下來,竟然不用除錯,難得。2017-6-16 21:26
//程式效率:耗時:159ms 記憶體:8535kb
#include <stdio.h>
#include <string.h>
#define INF 9999
struct node{
int to,next,w;
}e[6200*2+100];
int head[2500+100],cnt=0,vis[2500+100],d[2500+100];
void add(int u,int v,int w){//無向圖
cnt++,e[cnt].to=v,e[cnt].next=head[u],head[u]=cnt,e[cnt].w=w;//從頭插入,head[u]指向節點u對應的邊,cnt邊,e[cnt].to,cnt邊對應的終點,e[cnt].w,cnt邊對應的權重w
cnt++,e[cnt].to=u,e[cnt].next=head[v],head[v]=cnt,e[cnt].w=w;
}
int main(){
int t,c,ts,te,i,j,k,u,v,w,min;
memset(head,0,sizeof(head));
memset(vis,0,sizeof(vis));
scanf("%d%d%d%d",&t,&c,&ts,&te);
for(i=1;i<=c;i++){
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);
}
for(i=1;i<=t;i++)
d[i]=INF;
d[ts]=0;
for(i=1;i<=t;i++){//剩下t個點
u=0,min=INF;
for(j=1;j<=t;j++)
if(vis[j]==0&&d[j]<min){//找d[j]中的最小值
min=d[j];
u=j;
}
vis[u]=1;
k=head[u];//k是邊
while(k!=0){//鄰接表處理
v=e[k].to;
if(vis[v]==0&&d[u]+e[k].w<d[v])
d[v]=d[u]+e[k].w;
k=e[k].next;
}
}
printf("%d\n",d[te]);
return 0;
}
//1379 熱浪(heatwv)
//P1339 [USACO09OCT]熱浪Heat Wave
http://blog.csdn.net/mrcrack/article/details/70112975
//準備試試SPFA演算法,這篇文章介紹得不錯http://blog.csdn.net/muxidreamtohit/article/details/7894298
//鄰接表方式
//樣例很快通過,提交,測試點3,7,8,10WA
//查出的問題還不少,主要有兩處:vis[u]=0;//2 漏了此句
//if(vis[v]==0){//3 整個if語句寫到上面if語句的外面,寫錯位置了 提交AC
#include <stdio.h>
#include <string.h>
#define INF 9999;
struct node{
int to,next,w;
}e[6200*2+100];
int q[2500+100],h,t,cnt=0,head[2500+100],vis[2500+10],d[2500+10];
void add(int u,int v,int w){//無向圖,加入邊,採用鄰接表形式
cnt++,e[cnt].to=v,e[cnt].w=w,e[cnt].next=head[u],head[u]=cnt;
cnt++,e[cnt].to=u,e[cnt].w=w,e[cnt].next=head[v],head[v]=cnt;
}
int main(){
int t,c,ts,te,i,j,u,v,w,b;
memset(head,0,sizeof(head));
memset(vis,0,sizeof(vis));
scanf("%d%d%d%d",&t,&c,&ts,&te);
for(i=1;i<=c;i++){
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);
}
for(i=1;i<=t;i++)
d[i]=INF;
d[ts]=0;
h=t=1;
q[t]=ts;
vis[ts]=1;
t++;
while(h<t){
u=q[h];
b=head[u];
while(b!=0){
v=e[b].to;
if(d[v]>d[u]+e[b].w){//1 此處寫成 if(d[v]<d[u]+e[b].w)低階錯誤
d[v]=d[u]+e[b].w;
if(vis[v]==0){//3 整個if語句寫到上面if語句的外面,寫錯位置了
vis[v]=1;
q[t]=v;
t++;
}
}
b=e[b].next;
}
vis[u]=0;//2 漏了此句
h++;
}
printf("%d\n",d[te]);
return 0;
}
2017-6-18 13:54 補充SPFA演算法。
//1380 分糖果(candy)
//感覺與樹的深度有關
//即糖果從樹根下落,每一層上的小朋友都要得到糖果,糖果最多能到的層數
//大致有了基本思路,算最短路徑,之後將路徑排序,按由小到大的路徑進行糖果分配
//該題的關鍵,又到了最短路徑,問題是:1≤n≤100000 如何儲存邊的資料?
//c的資料沒有給定範圍,這樣,資料先開到系統能承受的範圍
//採用鄰接表,SPFA演算法
//樣例通過,提交,測試點7-8答案錯誤,測試點9-10執行錯誤
//http://codevs.cn/problem/2197/裡提交AC
//將 e[maxn*10] 改成 e[maxn*200] 提交AC 2017-12-23 17:31
//經測試 陣列需開到 e[maxn*20];
#include <stdio.h>
#include <string.h>
#define maxn 100100
#define INF 999999999
int n,p,c,m,head[maxn],cnt=0,q[maxn*10],d[maxn],vis[maxn];
struct node{
int to,next,w;
}e[maxn*20];//對 e[maxn*10] 資料範圍心存疑慮
void add_edge(int u,int v,int w){
cnt++,e[cnt].to=v,e[cnt].next=head[u],e[cnt].w=w,head[u]=cnt;
}
void SPFA(int s){
int i,u,v,b,h,t;
for(i=1;i<=n;i++)d[i]=INF;
d[s]=0,h=t=1,vis[s]=1,q[t]=s,t++;
while(h<t){
u=q[h];
for(b=head[u];b;b=e[b].next){
v=e[b].to;
if(d[v]>d[u]+e[b].w){
d[v]=d[u]+e[b].w;
if(vis[v]==0){
q[t]=v,t++,vis[v]=1;
}
}
}
h++;
}
}
int main(){
int i,u,v,max=0,j;
memset(head,0,sizeof(head)),memset(vis,0,sizeof(vis));
scanf("%d%d%d%d",&n,&p,&c,&m);
for(i=1;i<=p;i++){
scanf("%d%d",&u,&v);
add_edge(u,v,1),add_edge(v,u,1);
}
SPFA(c);
for(i=1;i<=n;i++)
if(d[i]>max)max=d[i];
printf("%d",max+m+1);
return 0;
}
//1381 城市路(Dijkstra)
//看了資料範圍,1<=n<=2000 1<=m<=10000鄰接表儲存圖比較合適
//樣例通過,提交,測試點5,7,9,10,11答案錯誤
//突然想到無向圖,邊數要*2,提交,測試點5 答案錯誤
//用輸出結果全為-1測試了一下,發現,測試點全部錯誤
//急需 測試點5 資料,或他人程式碼,搜尋網路無果,重新讀題,偶然發現"當然也可能有多條"
//立馬明白,在多條中,選擇最短一條。
//重改程式碼,將鄰接表改成鄰接矩陣
//修改,提交AC 2017-11-27
//在想,遇到重邊,用鄰接表如何處理
//對鄰接表如何處理,進行了深入思考,實現,沒問題,但是相對鄰接矩陣麻煩多了
#include <stdio.h>
#include <string.h>
#define INF 999999999
int a[2100][2100],cnt=0,n,m,d[2100],vis[2100];
int findMin(){
int i,k,min=999999999;
for(i=1;i<=n;i++)
if(vis[i]==0&&d[i]<min)min=d[i],k=i;
return k;
}
void Dijkstra(){
int i,count=1,k;
for(i=1;i<=n;i++)d[i]=a[1][i];
vis[1]=1;
while(count<n){
count++;
k=findMin(),vis[k]=1;
for(i=1;i<=n;i++)
if(vis[i]==0&&d[i]>d[k]+a[k][i])d[i]=d[k]+a[k][i];
}
}
int main(){
int i,j,u,v,w;
memset(vis,0,sizeof(vis));
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(i==j)a[i][j]=0;
else a[i][j]=INF;
for(i=1;i<=m;i++){
scanf("%d%d%d",&u,&v,&w);
if(a[u][v]>w)a[u][v]=w,a[v][u]=w;//多條邊處理
}
Dijkstra();
if(d[n]==INF)printf("-1");
else printf("%d",d[n]);
return 0;
}
//1381 城市路(Dijkstra)
// 一直對 鄰接表 如何處理 重邊念念不忘,天天想,翻資料,偶然間想到了解決方法,初始化d[i]時要注意,其他處理手法照舊。修改程式碼,提交AC 2017-11-30
#include <stdio.h>
#include <string.h>
#define INF 999999999
int head[2100],cnt=0,n,m,d[2100],vis[2100];
struct node{
int to,w,next;
}e[30200];//此處寫成 e[10100]
void add_edge(int u,int v,int w){
cnt++,e[cnt].to=v,e[cnt].w=w,e[cnt].next=head[u],head[u]=cnt;
}
int findMin(){
int i,k,min=999999999;
for(i=1;i<=n;i++)
if(vis[i]==0&&d[i]<min)min=d[i],k=i;
return k;
}
void Dijkstra(){
int i,b,u,v,count=1,k,w;//b邊
for(i=1;i<=n;i++)d[i]=INF;
d[1]=0,vis[1]=1;
for(b=head[1];b;b=e[b].next){
v=e[b].to;
if(d[v]>e[b].w) d[v]=e[b].w;//新增此行判斷,處理重邊 針對測試點5
}
while(count<n){
count++;
k=findMin(),vis[k]=1;
for(b=head[k];b;b=e[b].next){
v=e[b].to,w=e[b].w;
if(vis[v]==0&&d[v]>d[k]+w)d[v]=d[k]+w;
}
}
}
int main(){
int i,j,u,v,w;
memset(head,0,sizeof(head)),memset(vis,0,sizeof(vis));
scanf("%d%d",&n,&m);
for(i=1;i<=m;i++){
scanf("%d%d%d",&u,&v,&w);
add_edge(u,v,w),add_edge(v,u,w);//無向圖
}
Dijkstra();
if(d[n]==INF)printf("-1");
else printf("%d",d[n]);
return 0;
}//1382 最短路(Spfa)
//有幸再次編寫該題,沒有翻任何資料,一把成功AC,編的過程中,不斷有記憶湧現,一些易錯的點全部湧現出來,感覺這是能力記憶的體現,化為自身的能力了。2018-9-19 21:18
#include <stdio.h>
#include <string.h>
#define maxm 500100
#define maxn 100100
#define INF 900000000
int head[maxn],cnt=0,n,m,q[10*maxn],d[maxn],vis[maxn];
struct node{
int to;
int w;
int next;
}e[maxm*2];
void addEdge(int u,int v,int w){//無向圖
cnt++,e[cnt].to=v,e[cnt].w=w,e[cnt].next=head[u],head[u]=cnt;
}
void spfa(){
int h,t,u,v,w,b,i;
memset(vis,0,sizeof(vis));
for(i=1;i<=n;i++)d[i]=INF;
d[1]=0;
h=t=0;
q[t]=1,vis[1]=1,t++;
while(h<t){
u=q[h];
b=head[u];
while(b){
v=e[b].to;
w=e[b].w;
if(vis[v]==0&&d[v]>d[u]+w){
d[v]=d[u]+w;
q[t]=v;
t++;
}
b=e[b].next;
}
vis[u]=0;
h++;
}
printf("%d\n",d[n]);
}
int main(){
int i,j,u,v,w;
memset(head,0,sizeof(head));
scanf("%d%d",&n,&m);
for(i=1;i<=m;i++){
scanf("%d%d%d",&u,&v,&w);
addEdge(u,v,w),addEdge(v,u,w);
}
spfa();
return 0;
}
//1382 最短路(Spfa)
//樣例通過,提交,測試點3 執行超時
//參考了《資訊學奧賽一本通(C++版)》將 q[100000+100] 改成 q[100000*10+100]
//仔細一想確實如此,因一個點可能多次放入佇列中,故佇列開到點的10倍為好,提交AC 2017-12-22
//至此,該題已被擱置10天之久。
#include <stdio.h>
#include <string.h>
#define INF 999999999;
struct node{
int to,next,w;
}e[500000*2+100];
int q[100000*10+100],h,t,cnt=0,head[100000+100],vis[100000+10],d[100000+10];//q[100000+100]測試點3 執行超時
void add(int u,int v,int w){//無向圖,加入邊,採用鄰接表形式
cnt++,e[cnt].to=v,e[cnt].w=w,e[cnt].next=head[u],head[u]=cnt;
cnt++,e[cnt].to=u,e[cnt].w=w,e[cnt].next=head[v],head[v]=cnt;
}
int main(){
int n,m,i,j,u,v,w,b;
memset(head,0,sizeof(head));
memset(vis,0,sizeof(vis));
scanf("%d%d",&n,&m);
for(i=1;i<=m;i++){
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);
}
for(i=1;i<=n;i++)
d[i]=INF;
d[1]=0;
h=t=1;
q[t]=1;
vis[1]=1;
t++;
while(h<t){
u=q[h];
b=head[u];
while(b!=0){
v=e[b].to;
if(d[v]>d[u]+e[b].w){//1 此處寫成 if(d[v]<d[u]+e[b].w)低階錯誤
d[v]=d[u]+e[b].w;
if(vis[v]==0){//3 整個if語句寫到上面if語句的外面,寫錯位置了
vis[v]=1;
q[t]=v;
t++;
}
}
b=e[b].next;
}
vis[u]=0;//2 漏了此句
h++;
}
printf("%d\n",d[n]);
return 0;
}
2017-12-24 21:46 AC 該節內容
第三節 圖的連通性問題
//1383 燒錄光碟(cdrom)
//樣例通過,提交,測試點7,8,9答案錯誤
//想新增入度進行描述,發現題中樣例都通不過。
//網上搜索了一通,http://blog.csdn.net/cherish0222/article/details/57079677也只有該程式碼能通過
//受到啟發,該題用並查集處理.
//程式碼重寫,經編寫,發現不成功,同樣,測試點7,8,9答案錯誤
//一通研究,發現程式碼像並查集,但又不是並查集。
//樣例通過,提交AC 2017-12-30 21:33
//覺得程式碼寫得不夠漂亮,還是決定再重寫程式碼。
//樣例通過,提交AC 2017-12-30 21:40
//提供一組輸入輸出資料
//輸入:
//12
//2 6 0
//3 0
//4 0
//5 0
//1 0
//7 0
//8 0
//9 0
//10 0
//1 0
//1 0
//1 0
//1 0
//輸出:
//3
#include <stdio.h>
#include <string.h>
int a[210][210],pre[210];//pre[i] i節點對應的根節點
int main(){
int n,i,j,k,ans=0;
memset(a,0,sizeof(a));
scanf("%d",&n);
for(i=1;i<=n;i++)pre[i]=i;
for(i=1;i<=n;i++)
while(scanf("%d",&j)&&j)a[i][j]=1;
for(i=1;i<=n;i++)
for(k=1;k<=n;k++)
for(j=1;j<=n;j++)
if(a[i][k]&&a[k][j])a[i][j]=1;
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(a[i][j])pre[j]=pre[i];
for(i=1;i<=n;i++)
if(pre[i]==i)ans++;
printf("%d",ans);
return 0;
}
//1384 珍珠(bead)
//http://www.oier.cc/ssoj2427%E7%8F%8D%E7%8F%A0/此文程式碼寫得真不賴
//樣例通過,提交AC 2017-12-30 22:18
#include <stdio.h>
#include <string.h>
int a[110][110];
int main(){
int i,j,k,u,v,n,m,ans=0;
memset(a,0,sizeof(a));
scanf("%d%d",&n,&m);
for(i=1;i<=m;i++)
scanf("%d%d",&u,&v),a[u][v]=1;
for(k=1;k<=n;k++)//類似Floyd演算法
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(a[i][k]&&a[k][j])//i重於k k重於j 推出 i重於j
a[i][j]=1;//i重於j
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
a[0][j]+=a[i][j],a[i][0]+=a[i][j];//a[0][j]統計重於j的珍珠個數 a[i][0]統計輕於i的珍珠個數
for(i=1;i<=n;i++)
if(a[0][i]>n/2||a[i][0]>n/2)
ans++;
printf("%d",ans);
return 0;
}
2017-12-30 22:18 AC 該節內容
第四節 並查集
//1346 【例4-7】親戚(relation)
//2017-11-11 23:05 AC
#include <stdio.h>
int f[20100];
int getf(int u){
if(f[u]==u)return u;
return f[u]=getf(f[u]);
}
void merge(int u,int v){
int f1=getf(u),f2=getf(v);
if(f1!=f2)
f[f2]=f1;
}
int main(){
int i,n,m,u,v,q;
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++)f[i]=i;
for(i=1;i<=m;i++){
scanf("%d%d",&u,&v);
merge(u,v);
}
for(i=1;i<=n;i++)f[i]=getf(i);//新增此句提高效率
scanf("%d",&q);
for(i=1;i<=q;i++){
scanf("%d%d",&u,&v);
if(f[u]==f[v])printf("Yes\n");
else printf("No\n");
}
return 0;
}
//1347 【例4-8】格子游戲
//此文介紹得不錯,http://blog.csdn.net/clove_unique/article/details/48682185摘抄如下:
//這道題讓我學會了用結構體實現二維的並查集。其實也並不是很難,在每一次比較的時候只需要把x和y都比較一下就可以了;
//每一次劃線,先判斷一下,如果起點在集合裡,終點也在集合裡,那麼符合條件,輸出當時的步數就可以了;如果不符合上面的條件,把點入集合;如果到最後還沒有符合條件的情況,輸出draw就可以了。
//樣例通過,修改,提交AC 2017-11-18 9:53
#include <stdio.h>
struct node{
int r,c;
}f[210][210],f1,f2;
struct node getf(struct node f3){
if(f[f3.r][f3.c].r==f3.r&&f[f3.r][f3.c].c==f3.c)return f3;
return f[f3.r][f3.c]=getf(f[f3.r][f3.c]);
}
int main(){
int n,m,i,j,r,c;
char cmd[5];
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
f[i][j].r=i,f[i][j].c=j;
for(i=1;i<=m;i++){
scanf("%d%d%s",&r,&c,cmd);
if(cmd[0]=='D'){
f1=getf(f[r][c]),f2=getf(f[r+1][c]);
}else if(cmd[0]=='R'){
f1=getf(f[r][c]),f2=getf(f[r][c+1]);
}
if(f1.r==f2.r&&f1.c==f2.c){
printf("%d",i);
return 0;
}else{//合併 左靠
f[f2.r][f2.c]=f1;
}
}
printf("draw");
return 0;
}
//1385 團伙(group)
//https://www.cnblogs.com/GXZlegend/p/6405309.html受啟發,開始編碼
//將n個人擴充到2*n個人,1-n與n+1-2n人對立
//該題,在1-n中找不同的爸爸個數
//AC 2017-11-12 22:39
#include <stdio.h>
#include <string.h>
int f[2100],vis[2100];
int getf(int u){
if(f[u]==u)return u;
return f[u]=getf(f[u]);
}
void merge(int u,int v){
int f1=getf(u),f2=getf(v);
if(f1!=f2)f[f2]=f1;
}
int main(){
int n,m,i,p,x,y,cnt=0,father;
memset(vis,0,sizeof(vis));
scanf("%d%d",&n,&m);
for(i=1;i<=2*n;i++)f[i]=i;
while(m--){
scanf("%d%d%d",&p,&x,&y);
if(p==0)merge(x,y);
else merge(x,y+n),merge(x+n,y);
}
for(i=1;i<=n;i++){
father=getf(i);
if(vis[father]==0)
vis[father]=1,cnt++;
}
printf("%d",cnt);
return 0;
}
//1386 打擊犯罪(black)
//"第一個整數表示該行除第一個外還有多少個整數"這句話花了些時間,對照輸入樣例總算弄明白了
//看了樣例的圖後,感覺這題在求關節點,似乎與並查集扯不上關係
//http://blog.csdn.net/u011123263/article/details/39010779此文介紹得不錯,程式碼也夠短,思路摘抄如下:
//題解:我們求刪點完後剩下的圖組成的集合,假設刪點刪到了k那剩下的圖就是由k~n之間的
//點組成,如果他們組成的結合最大子圖節點數不大(n+1)/2則說明k不該刪,則繼續往前推.(注意:刪除1~k)
//http://www.cnblogs.com/fujudge/p/7577741.html此文用鄰接表寫的,感覺很對胃,思路摘抄如下:
//不容易刪點,所以考慮倒著加點,找到一組不滿足要求了輸出即可。
//樣例通過,提交AC 2017-12-1 20:57
#include <stdio.h>
#include <string.h>
#define maxn 1010
struct node{
int to,next;
}e[maxn*maxn];
int head[maxn],cnt=0,f[maxn],size[maxn];
void add_edge(int u,int v){//鄰接表方式
cnt++,e[cnt].to=v,e[cnt].next=head[u],head[u]=cnt;
}
int getf(int u){//找爸爸
if(f[u]==u)return u;
return f[u]=getf(f[u]);
}
int main(){
int n,i,j,t,k,f1,f2,b;//b邊
memset(head,0,sizeof(head));
scanf("%d",&n);
for(i=1;i<=n;i++){
f[i]=i,size[i]=1;
scanf("%d",&t);
for(j=1;j<=t;j++){
scanf("%d",&k);
add_edge(i,k),add_edge(k,i);//無向圖
}
}
for(i=n;i>=1;i--){//逆向新增
f1=getf(i);
for(b=head[i];b;b=e[b].next){
j=e[b].to;
if(j>i){//在i之前的點
f2=getf(j);
if(f1!=f2){
f[f2]=f1;
size[f1]+=size[f2];
if(size[f1]>n/2){
printf("%d",i);
return 0;
}
}
}
}
}
return 0;
}
//1387 搭配購買(buy)
//粗看題目,覺得挺難的,但細細一讀,發現,屬同一個爸爸的都需要購買
//在買得起的集團中選價值最大的。
//提交,只有測試點1,8答案正確
//看了這篇文章http://blog.csdn.net/xiaofang3a/article/details/39324067的文字,才明白,想法確實有誤,摘抄如下
//買ui就必須買vi,同理,如果買vi就必須買ui。可以用並查集把這這物品些歸結到一起,形成一個新的物品,然後重新得到一系列物品,然後使用01揹包就OK了。
//此文http://blog.csdn.net/u011123263/article/details/39312835程式碼與本人相似較高,研究01揹包部分
//修改,提交AC。2017-11-20 22:17
//本題證明,並查集掌握爐火純青,但01揹包還有欠缺,尤其是一維陣列形式
#include <stdio.h>
#include <string.h>
int c[10100],d[10100],f[10100],dp[10100];
int max(int a,int b){
return a>b?a:b;
}
int getf(int u){
if(f[u]==u)return u;
return f[u]=getf(f[u]);
}
void merge(int u,int v){
int f1=getf(u),f2=getf(v);
if(f1!=f2)f[f2]=f1,c[f1]+=c[f2],d[f1]+=d[f2];
}
int main(){
int n,m,w,i,j,u,v;
memset(dp,0,sizeof(dp));//別忘了初始化
scanf("%d%d%d",&n,&m,&w);
for(i=1;i<=n;i++)f[i]=i;
for(i=1;i<=n;i++)scanf("%d%d",&c[i],&d[i]);
for(i=1;i<=m;i++){
scanf("%d%d",&u,&v);
merge(u,v);
}
for(i=1;i<=n;i++)getf(i);//更新最新的爸爸
for(i=1;i<=n;i++)
if(f[i]==i){
for(j=w;j>=c[i];j--)
dp[j]=max(dp[j],dp[j-c[i]]+d[i]);//01揹包的一維陣列優化要好好學學
}
printf("%d",dp[w]);
}
//1388 家譜(gen)
//該題的難點在於,資料是字串,如何將字串對映成數字是難點
//翻看了一下,基本上都要用到map,那好吧,開始學習。
//http://blog.csdn.net/xiaofang3a/article/details/39583367此文程式碼寫得夠好,map用得夠漂亮,值得學習
//用C++來編寫
//樣例通過,提交,測試點6,7,8答案錯誤
//洛谷 P2814 家譜 提交,同樣 測試點6,7,8 WA
//在正確程式碼的基礎上,進行程式碼修改,逐漸逼近本人程式碼,發現了問題所在,找到的爸爸可能還不是祖宗。
//修改,提交AC 2017-11-20
#include <iostream>
#include <string>
#include <map>
using namespace std;
map<string,string> f;
string getf(string a){
if(f[a]==a)return a;
return f[a]=getf(f[a]);
}
int main(){
string s,b,c,d;
while(cin>>s&&s!="$"){
if(s[0]=='#'){
b=s.substr(1,s.size()-1);
if(f[b]=="")f[b]=b;
}else if(s[0]=='+'){
c=s.substr(1,s.size()-1);
getf(b);
f[c]=f[b];
}else if(s[0]=='?'){
d=s.substr(1,s.size()-1);
getf(d);//漏了此句, 測試點6,7,8 WA
cout<<d<<" "<<f[d]<<endl;
}
}
return 0;
}
//1389 親戚
//樣例通過,提交AC,請注意,此刻,網路上還搜尋不到該題的解法。2017-11-20
#include <stdio.h>
int f[100100],cnt[100100];//cnt[i]統計以i為父親的家族人數
int getf(int a){
if(f[a]==a)return a;
return f[a]=getf(f[a]);
}
void merge(int a,int b){//左靠
int f1=getf(a),f2=getf(b);
if(f1!=f2)
f[f2]=f1,cnt[f1]+=cnt[f2];//此句很關鍵 cnt[f1]+=cnt[f2],自個想到的,真是很佩服自己
}
int main(){
int n,m,i,j,a,b;
char cmd[10];
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++)f[i]=i,cnt[i]=1;
while(m--){
scanf("%s",cmd);
switch(cmd[0]){
case 'M':
scanf("%d%d",&a,&b);
merge(a,b);
break;
case 'Q':
scanf("%d",&a);
printf("%d\n",cnt[getf(a)]);
break;
}
}
return 0;
}
//1390 食物鏈
2.//P2024 食物鏈
http://blog.csdn.net/mrcrack/article/details/70112975
//靠自己,想不到要分成三塊x的同類,x吃的動物,被x吃的動物
//f[x] f[x+n] f[x+2*n]x的同類,x吃的動物,吃x的動物
//f[y] f[y+n] f[y+2*n]y的同類,y吃的動物,吃y的動物
//審題不清,沒往腦子裡去:A 吃 B,B吃 C,C 吃 A。
//http://www.cnblogs.com/zbtrs/p/5819576.html分析得不錯,摘抄如下 :
//分析:吃與被吃和同類是三種邏輯關係,而三種邏輯關係對應的動物又有很多,而動物之間又可以形成集合,所以考慮並查集.因為有3種邏輯關係,所以用大小n*3的並查集.
//可以參考noip2010的關押罪犯,對於一個犯人而言,另一個犯人只有可能和他在同一個監獄或者在不同監獄,那麼建立n*2大小的並查集,那麼對於本題也是一樣,用x表示和x同種的動物集合,x+n表示被x吃的動物,x+2*n表示吃x的動物,那麼對於另一種動物y,如果是第一種說法,那麼x和y一定是同類(廢話......),那麼如果y在x+n的集合中或者y在x+2*n的集合中,就是假話,當然,要先判斷x或y是否大於n並且是否相等,之後合併一下x和y,x+n和y+n,x+2*n和y+2*n.
//那麼對於第二種說法呢?如果x和y是同類,那麼肯定是假話,如果y吃x,那麼肯定也是假話,那麼判斷x和y或者x+2*n和y是否在同一個集合即可,之後合併x和y + 2 * n,x + n和 y,x + 2*n和y + n(因為食物鏈是環,吃x的必然被y吃),那麼本題就結束了.
//提交30分,只AC了測試點1,3,9明白是判斷同類,異類出了問題。 修改,提交還是30分
//錯在:如果是第一種說法,那麼x和y一定是同類(廢話......),那麼如果y在x+n的集合中或者y在x+2*n的集合中,就是假話
//錯在:那麼對於第二種說法呢?如果x和y是同類,那麼肯定是假話,如果y吃x,那麼肯定也是假話
//歸根結底,對題目分析不夠,望日後有重做的機會2017-6-4 23:18
#include <stdio.h>
int f[3*50000+100];
int getf(int z){
if(f[z]==z)
return z;
f[z]=getf(f[z]);
return f[z];
}
void merge(int a, int b){//靠左規則
int f1=getf(a),f2=getf(b);
if(f1!=f2)
f[f2]=f1;
}
int main(){
int n,k,i,j,x,y,t,ans=0;
scanf("%d%d",&n,&k);
for(i=1;i<=3*n;i++)
f[i]=i;
for(i=1;i<=k;i++){
scanf("%d%d%d",&t,&x,&y);
if(x>n||y>n)
ans++;
else if(t==1){
if(getf(x+n)==getf(y)||getf(x+2*n)==getf(y))//2getf(x+n)==getf(y)||getf(x)==getf(y+n) x吃y 或者 y吃x 非同類 1getf(x+n)==getf(y)||getf(x+2*n)==getf(y+n)||getf(x)==getf(y+2*n)
ans++;
else{
merge(x,y);
merge(x+n,y+n);
merge(x+2*n,y+2*n);
}
}else if(t==2){
if(getf(x)==getf(y)||getf(x+2*n)==getf(y))//2getf(x)==getf(y)同類 同類1getf(x)==getf(y)||getf(x+n)==getf(y+n)||getf(x+2*n)==getf(y+2*n)
ans++;
else{
merge(x+n,y);
merge(x+2*n,y+n);
merge(x,y+2*n);
}
}
}
printf("%d\n",ans);
return 0;
}
2017-12-1 20:57 AC 該節內容
第五節 最小生成樹
//1348 【例4-9】城市公交網建設問題
//使用Prim演算法未果,多次修改均無效,網上搜索了一堆程式碼,發現,全是無法AC的程式碼。
//採用Kruskal演算法
//很快樣例通過,提交AC 2017-12-4
//該題有幾點要注意:
//輸出,按邊的第一個點的序號自小到大輸出,若第一個序號相同,按第二個點的序號自小到大輸出
//要列印加入路徑,Kruskal演算法絕對要好過Prim演算法,Prim演算法與Dijkstra演算法比較接近。2017-12-4
#include <stdio.h>
int f[110];
struct node{
int a,b,w;
}e[110*110],e_t,d[110];
int getf(int u){
if(f[u]==u)return u;
return f[u]=getf(f[u]);
}
int merge(int u,int v){
int f1=getf(u),f2=getf(v);
if(f1!=f2){
f[f2]=f1;
return 1;
}
return 0;
}
void quicksort(int left,int right){//自小到大排列
int i=left,j=right,mid=e[(left+right)/2].w;
while(i<=j){
while(e[i].w<mid)i++;
while(e[j].w>mid)j--;
if(i<=j)e_t=e[i],e[i]=e[j],e[j]=e_t,i++,j--;
}
if(i<right)quicksort(i,right);
if(left<j)quicksort(left,j);
}
int main(){
int n,m,i,j,u,v,w,t,cnt=0;
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++)f[i]=i;
for(i=1;i<=m;i++){
scanf("%d%d%d",&u,&v,&w);
if(u>v)t=u,u=v,v=t;//讓小的點在前面
e[i].a=u,e[i].b=v,e[i].w=w;
}
quicksort(1,m);
for(i=1;i<=m;i++)
if(merge(e[i].a,e[i].b)){
cnt++;
d[cnt].a=e[i].a,d[cnt].b=e[i].b,d[cnt].w=e[i].w;
if(cnt==n-1)break;
}
for(i=1;i<=cnt;i++)//自小到大排序
for(j=i+1;j<=cnt;j++)
if(d[i].a>d[j].a)e_t=d[i],d[i]=d[j],d[j]=e_t;
else if(d[i].a==d[j].a&&d[i].b>d[j].b)e_t=d[i],d[i]=d[j],d[j]=e_t;
for(i=1;i<=cnt;i++)
printf("%d %d\n",d[i].a,d[i].b);
return 0;
}
//1349 【例4-10】最優佈線問題
//最小生成樹 採用Prim演算法
//樣例通過,提交,只有測試點1答案正確,靜態檢查程式碼,發現 scanf("%d",&n);//此處寫成 scanf("%d%d",&n);只對了測試點1
//修改,提交AC 2017-12-3 21:28
#include <stdio.h>
#include <string.h>
#define INF 999999999
int vis[110],d[110],a[110][110],n;//d[]到生成樹的最短距離
int findMin(){//返回未訪問過的最小的d[i]的i值
int i,j,min=999999999;
for(i=1;i<=n;i++)
if(vis[i]==0&&d[i]<min)min=d[i],j=i;
return j;
}
void Prim(){
int i,j,k;
memset(vis,0,sizeof(vis));
for(i=1;i<=n;i++)d[i]=a[1][i];
for(i=1;i<=n;i++){//n個點
k=findMin(),vis[k]=1;
for(j=1;j<=n;j++)
if(vis[j]==0&&d[j]>a[k][j])d[j]=a[k][j];
}
}
int main(){
int i,j,u,v,w,sum=0;
scanf("%d",&n);//此處寫成 scanf("%d%d",&n);只對了測試點1
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
scanf("%d",&a[i][j]);
Prim();
for(i=1;i<=n;i++)sum+=d[i];
printf("%d",sum);
return 0;
}
//1350:【例4-11】最短網路(agrinet)
//Kruskal
//沒有參考任何資料,獨立編寫,往日的一些注意事項湧現出來,很成功,一把AC。
//仔細思考了 並查集 在此種演算法中的作用。
//程式碼編寫還是花了些時間,主要花在思考上。2018-9-19 22:20
#include <stdio.h>
int n,b=0,f[110];
struct node{
int u,v,w;
}e[100*100/2