2. 程式人生 > >基數估計演算法(二)：Linear Counting演算法

基數估計演算法(二)：Linear Counting演算法

阿新 • • 發佈：2019-01-30

簡介

Linear Counting是KYU-YOUNG WHANG，BRAD T. VANDER-ZANDEN和HOWARD M. TAYLOR大佬們1990年發表的論文《A linear-time probabilistic counting algorithm for database applications》中提出的基於概率的基數估計演算法。

基本思想及實現

Linear Counting的實現方式非常簡單。
首先定義一個hash函式：
function hash(x): -> [0,1,2,…,m-1]，假設該hash函式的hash結果服從均勻分佈。

接著定義一個長度為m的bit陣列，開始每一位上都初始化為0.

然後對可重複集合裡的每個元素進行hash得到k，如果bitmap[k]為0則置1。

最後統計bitmap數組裡為0的位數u。

設集合基數為n，則有：
n^=−mlnum，且其為n的最大似然估計。

簡單的虛擬碼如下：
BLC虛擬碼

舉個例子說明下吧，如下：

LC示例
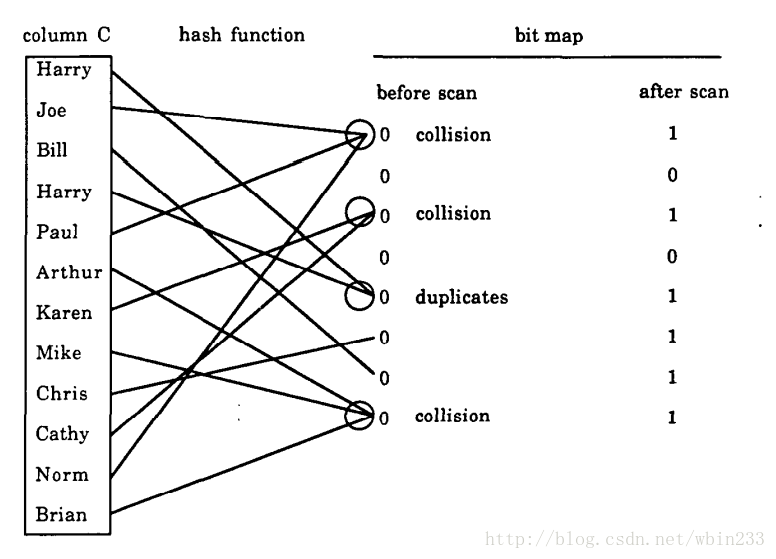
集合中共有11個元素，hash函式對映到[0,7]中（m=8）且結果服從均勻分佈。如圖hash結果後共有2個bit為0，即u=2。代入上述公式可得估計結果為11.1(實際值為10)。
【該例子只為了說明演算法的過程，實際中都是大資料中估計。】

公式證明

先說明下述中使用到的變數。

變數 含義
n 基數
q 總數
m bit陣列的長度（hash區間）
t n/m
Un hash後bit陣列為0的位數
Vn Un/m
p E(Vn)

由於hash函式對映後的hash結果服從均勻分佈，因此任意一數選中bitmap陣列的某一個bit概率為1m。
設Aj為事件“經過n個不同元素雜湊後，第j個桶值為0”，則：
P(Aj)=(1−1m)n,
P(Aj∩Ak)=(1−2m)n,j≠k.

又每個bit是相互獨立的，即Aj服從均勻分佈。
則Un的數學期望為：
E(Un)=∑mj=1P(Aj)=m(1−1m)n=m(((1+

1−m)−m)−nm)≅me−nm=me−t,當n,m→∞

【數學上證明：limx→∞(1+1x)x=e】

所以：E(Un)=me−nm

即：n=−mlnE(Un)m

顯然，bitmap裡每個bit的值服從相同的0-1分佈，因此Un服從二項分佈。
由概率論與數理統計知識可知，當n很大時，可以用正態分佈逼近二項分佈，因此可以認為當n和m趨於無窮大時Un漸進服從正態分佈。
由於我們觀察到的空桶數Un是從正態分佈中隨機抽取的一個樣本，因此它就是μ的最大似然估計（正態分佈的期望的最大似然估計是樣本均值）。

又由如下定理：

設f(x)是可逆函式且x^是x的最大似然估計，則f(x^)是f(x)的最大似然估計。
且−mlnxm是可逆函式，則n^=−mlnUnm是 n=−mlnE(Un)m的最大似然估計。

Un和Vn的期望和方差

先給出結論，在m,n→∞的前提下有：
E(Un)=me−nm=me−t.

Var(Un)=me−t(1−(1+

相關推薦

基數估計演算法(二)：Linear Counting演算法

簡介 Linear Counting是KYU-YOUNG WHANG，BRAD T. VANDER-ZANDEN和HOWARD M. TAYLOR大佬們1990年發表的論文《A linear-time probabilistic counting

基數估計演算法(一)：Flajolet-Martin演算法

簡介 基礎版 標準版 TIPs 參考資料 簡介 說起基數估計演算法的始祖，或許就是由Flajolet和Martin大佬發表的論文《 Probabilistic counting algorithms for data base appli

排序演算法二：快速排序

#include <stdio.h> #include <stdlib.h> #include <string.h> #include <time.h>

Python排序演算法[二]：測試資料的迷霧散去

演算法試驗中不僅僅要嘗試使用不同的寫法，更要注意測試所用資料的規律性，它們都會直接影響測試結果。 在上一篇文章《Python 排序演算法[一]：令你茅塞頓開，卻又匪夷所思》中我們學習了排序演算法中比較費時間的三種：氣泡排序、選擇排序、插入排序。並且在測試過程中發現了匪夷所思的問題，但是這都難不倒諸

機器學習演算法二：詳解Boosting系列演算法一Adaboost

本文主要介紹boosting演算法得基本原理，以及的三種典型演算法原理：adaboost，GBM（Gradient bossting machine），XGBoost。 Boosting方法原理 boosting演算法是一類將弱學習器提升為強學習器的整合學習

五大常用演算法之二： 動態規劃演算法1

非常有必要看一看：一、基本概念    動態規劃過程是：每次決策依賴於當前狀態，又隨即引起狀態的轉移。一個決策序列就是在變化的狀態中產生出來的，所以，這種多階段最優化決策解決問題的過程就稱為動態規劃。二、

Alink漫談(十二) ：線上學習演算法FTRL 之 整體設計

# Alink漫談(十二) ：線上學習演算法FTRL 之 整體設計 [Toc] ## 0x00 摘要 Alink 是阿里巴巴基於實時計算引擎 Flink 研發的新一代機器學習演算法平臺，是業界首個同時支援批式演算法、流式演算法的機器學習平臺。本文和下文將介紹線上學習演算法FTRL在Alink中是如何實現

演算法(八)：圖解KNN演算法

演算法簡介 K最相鄰演算法(K-NearestNeighbor Classification Algorithm,KNN)是資料探勘分類技術中最簡單的方法之一,所謂K最近鄰，就是K個最近的鄰居的意思，說的是每個樣本都可以用它最接近的K個鄰居來代表。 KNN演算法的核心思想是如果一個樣本在特徵空間中的K個最

優化演算法1：模擬退火演算法思想解析

1.演算法簡介 模擬退火演算法得益於材料的統計力學的研究成果。統計力學表明材料中粒子的不同結構對應於粒子的不同能量水平。在高溫條件下，粒子的能量較高，可以自由運動和重新排列。在低溫條件下，粒子能量較低。如果從高溫開始，非常緩慢地降溫（這個過程被稱為退火），粒子

A.pro讀演算法の2：高精度演算法

1.1 描述 高精度演算法，屬於處理大數字的數學計算方法。在一般的科學計算中，會經常算到小數點後幾百位或者更多，當然也可能是幾千億幾百億的大數字。一般這類數字我們統稱為高精度數，高精度演算法是用計算機對於超大資料的一種模擬加，減，乘，除，乘方，階乘，開方等運算。對於非常龐大

tensorflow基本演算法(2)：最近鄰演算法nearest neighbor

參考維基百科： 在模式識別領域中，最近鄰居法（KNN演算法，又譯K-近鄰演算法）是一種用於分類和迴歸的非引數統計方法。在這兩種情況下，輸入包含特徵空間中的k個最接近的訓練樣本。 在k-NN分類中，輸出是一個分類族群。一個物件的分類是由其鄰居的“多數表決”確定的，k個最近鄰

演算法隨筆：動態規劃演算法實現DNA序列對齊

背景：專業寫作課的實驗專案專案背景：利用動態規劃演算法的思想實現DNA的序列最優對齊演算法思路：暫時略註明：兩小時寫兩小時調程式碼，請尊重博主原創。同一課程的看到了是不是應該加個關注，hhh。轉載請註明出處：https://blog.csdn.net/whandwho/art

資料探勘經典演算法之：C4.5演算法

一.C4.5演算法 C4.5演算法是對ID3演算法的一種改進，所以，首先我們來看ID3演算法。 ID3演算法是在決策樹各個結點上應用資訊增益準則來選擇特徵，遞迴地構建決策樹。 決策樹：是一種基本的分類與迴歸方法，一種分類決策模型，是一種樹形結構，該模型具有可讀性，分類速

演算法05：二分搜尋演算法——分治法Part1

摘自網路： 分治法的設計思想是，將一個難以直接解決的大問題，分割成一些規模較小的相同問題，以便各個擊破，分而治之。 分治法所能解決的問題一般具有以下幾個特徵： 1.該問題的規模縮小因為問題的計算複雜性一般是隨著問題規模的增加 2.該問題可以分解為若干個規模較小的相同問題，即

機器學習演算法篇：最大似然估計證明最小二乘法合理性

最小二乘法的核心思想是保證所有資料誤差的平方和最小，但我們是否認真思考過為什麼資料誤差平方和最小便會最優，本文便從最大似然估計演算法的角度來推導最小二乘法的思想合理性，下面我們先了解一下最大似然估計和最小二乘法，最後我們通過中心極限定理剋制的誤差ε服從正態分佈

聚類演算法之DBSCAN演算法之二：高維資料剪枝應用NQ-DBSCAN

一、經典DBSCAN的不足 1.由於“維度災難”問題，應用高維資料效果不佳 2.執行時間在尋找每個點的最近鄰和密度計算，複雜度是O(n2)。當d>=3時，由於BCP等數學問題出現，時間複雜度會急劇上升到Ω（n的四分之三次方）。 二、DBSCAN在高維資料的改進 目前的研究有

hihocoder 1089 最短路徑·二：Floyd演算法

http://hihocoder.com/problemset/problem/1089 描述 萬聖節的中午，小Hi和小Ho在吃過中飯之後，來到了一個新的鬼屋！ 鬼屋中一共有N個地點，分別編號為1..N，這N個地點之間互相有一些道路連通，兩個地點之間可能有多條道路連通，但是並不存在一

雜湊學習演算法之二：基於hash的ANN框架

在上一節瞭解了ANN的背景，簡單介紹了hash的演算法，那基於hash的ANN框架是怎樣的呢？ 框架圖 框架說明 基於hash的ANN主要有四個步驟，包括特徵提取、hash編碼（學習+編碼）、漢明距離排序、重排序。 1、特徵提取 有查詢影象和影象資料庫，需要對這兩類分別

SSE影象演算法優化系列二十三: 基於value-and-criterion structure 系列濾波器（如Kuwahara，MLV，MCV濾波器）的優化。 SSE影象演算法優化系列十四：區域性均方差及區域性平方差演算法的優化 SSE影象演算法優化系列七：基於SSE實現的極速的矩形核腐蝕和膨脹（

       基於value-and-criterion structure方式的實現的濾波器在原理上其實比較簡單，感覺下面論文中得一段話已經描述的比較清晰了，直接貼英文吧，感覺翻譯過來反而失去了原始的韻味了。        T

演算法二十二：陣列和之間差最小

有兩個序列a,b，大小都為n,序列元素的值任意整數，無序； 要求：通過交換a,b中的元素，使[序列a元素的和]與[序列b元素的和]之間的差最小。 例如:  var a=[100,99,98,1,2, 3]; var b=[1, 2, 3, 4,5,40]; 分析：要是序