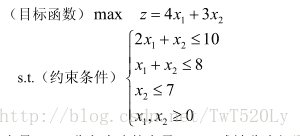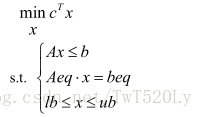1.線性規劃簡介

線性規劃（LP）是數學規劃的一個分支。

x1,x2為決策變數，約束條件記為s.t.（subject to）。

2.線性規劃的matlab標準形式

線性規劃的目標函式可以求最大值也可以求最小值，約束條件的不等號可以是小於號也可以是大於號，因此在matlab中給出了統一形式。

其中c和x均為n維列向量，A、Aeq為適當維數（列數與x維數相同，行數與約束條件數相同）,b、beq為適當維數的列向量（維數與約束條件數相同）。

例如：
maxcTxs.t.Ax≥b$max{c}^{T}xs.t.Ax\ge b$

matlab中為：
min−cTxs.t.−Ax≤b$min-c^{T}x$

3.線性規劃中解的概念

可行解：滿足約束條件的 解x = （x1,x2…xn），稱為線性規劃問題的可行解，從而使目標函式達到最大值或者最小值的可行解稱為最優解。
可行域：所有可行解構成的集合稱為問題的可行域，記為R。

4.一般的線性規劃問題

在一般的n維空間中，滿足 ∑ni=1aixi=b$\sum _{i=1}^n{a}_i{x}_i=b$ 的點集稱為一個超平面，而滿足 ∑ni=1aixi≥b$\sum _{i=1}^n{a}_i{x}_i\ge b$ （或者∑ni=1aixi≤b$\sum _{i=1}^n{a}_i{x}_i\le b$ ）的點集稱為一個半平面，若干個半平面的交集稱為多胞形，有界的多胞形稱為多面體。因此線性規劃的可行域必定為多胞形（空集也視為多胞形）。若該區域R為凸集，則凸集中的任意兩點的連線必然在該凸集中，若x為區域R的極點，則x不能位於R中的任意兩點的連線上。

5.matlab中線性規劃求解過程

① 利用linprog函式返回最小值解向量。
② value = c’ * x求最小值。

基本函式形式是 linprog(c,A,b) , c用於確定等值線（列向量），返回值為向量x。
其他的函式形式：
[x,fval]=linprog(c,A,b,Aeq,beq,LB,UB,x0,OPTIONS)
x0為向量x的初始值，一般使用zeros()函式 初始化，LB和UB分別是向量x的下界向量和上界向量。返回值為fval（目標函式c’ * x的值）。

6.常見技巧

問題為：

min|x1|+|x2|+…+|xn|s.t.Ax≤b$min|x_1|+$

轉換為：
min∑ni=1(ui+vi)$min\sum _{i=1}^n(u_i+v_i)$
s.t.{A(ui−vi)≤b,u,v≥0,$s.t.\{\begin{array}{l}A(u_i-v_i)\le b,\\ u,v\ge 0,\end{array}$

7.運輸問題（產銷平衡）

8.指派問題

1.數學模型

2.利用匈牙利演算法
演算法主要思想：如果係數矩陣中C=(cij$c_{ij}$)一行（或一列）中每一個元素都加上或減去同一個數，得到新矩陣B，則以B或C為係數矩陣的指派問題具有相同的最優指派。
最優指派的結果是一個2行n列的行列式，第一行為第i人，第二行為被指派的地點。
求解中心：變換出n個不同行不同列的零元素。