• 注：子序列(subsequence)不同於子串(substring)，子串必須相鄰，子序列不必相鄰。e.g.”ACE” is a subsequence of “ABCDE” while “AEC” is not.

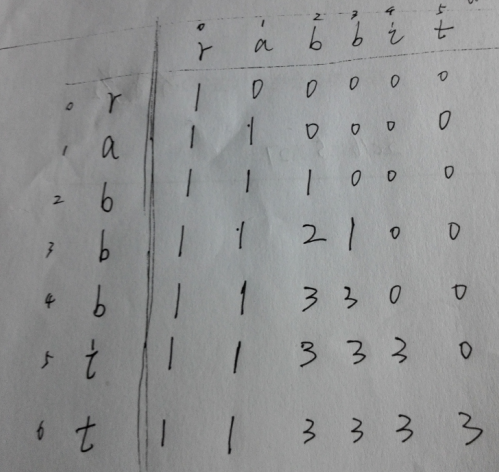
-樣例：S = “rabbbit”, T = “rabbit”，Return 3.

-思路：如果直接dfs的話肯定會超時，想辦法劃分成子問題。S中包含的T的數目與S-1中包含的T的數目似乎有一定的關係。

如果用dp[i][j] 表示s[0:i]中包含t[0:j]的數目的話，當s[i]==t[j]時，t[j]可以和s[i]匹配，此時有dp[i-1][j-1]種情況，t[j]也可以不和s[i]匹配，此時有dp[i-1][j]種情況，於是有如下的動態轉移方程：

-程式碼如下

class Solution {
public:
    int numDistinct(string s, string t) {
        if(t == "")  return 1;
        if(s == "")  return 0;
        vector<int> tmp(t.size(),0);
        vector<vector<int> > dp(s.size(),tmp);
        for
 
(int i=0; i<s.size(); ++i){
            for(int j=0; j<t.size(); ++j){
                if(i == 0){
                    if(j == 0){
                        dp[i][j] = (s[i] == t[j]) ? 1 : 0;
                    }
                }else if(j == 0){
                    dp[i][j] = dp[i-1][j] + ((s[i] == t[j])?1
 
:0);
                }else{
                    dp[i][j] = dp[i-1][j] + ((s[i] == t[j])?dp[i-1][j-1] : 0);
                }
            }
        }
        return dp[s.size()-1][t.size()-1];
    }
};

-優化
由於dp[i][j]只與dp[i-1][j]和dp[i-1][j-1]有關，因此我們只需儲存前面一行的值就可以計算出當前行的值，節省了空間；另外，當 i < j時，dp[i][j]必然等於0，節省了時間。優化後的程式碼如下：

class Solution {
public:
    int numDistinct(string s, string t) {
        if(t == "")  return 1;
        if(s == "")  return 0;
        vector<int> tmp(t.size(),0);
        vector<vector<int> > dp(2,tmp);   // 只與dp[i-1][j], dp[i-1][j-1]有關
        dp[0][0] = (s[0] == t[0]) ? 1 : 0;
        for(int i=1; i<s.size(); ++i){
            int n = min((int)t.size()-1,i);
            for(int j=0; j<=n; ++j){
                if(j == 0){
                    dp[i&1][j] = dp[1^(i&1)][j] + ((s[i] == t[j])?1:0);
                }else{
                    dp[i&1][j] = dp[1^(i&1)][j] + ((s[i] == t[j])?dp[1^(i&1)][j-1] : 0);
                }
            }
        }
        return dp[(s.size()-1)&1][t.size()-1];
    }
};