演算法過程：
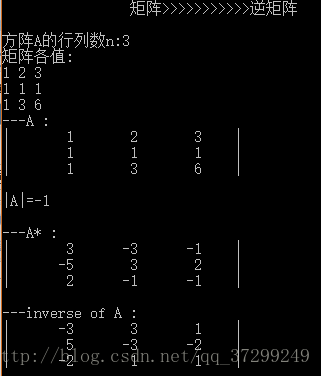
-計算 判斷|A|是否為0
-利用原矩陣生成A*（伴隨）矩陣，具體：A*二維陣列中第[i][j]個元素，除去該行該列，其他元素進入臨時陣列，計算臨時陣列行列式值，即為A*[i][j]

最後矩陣A*/|A| 即為該矩陣的逆矩陣

原始碼：

#include<iostream>
#include<iomanip>
#include<cmath>
using namespace std;
//By Vove.

float Cal_Det(float s[9][9],int n);//計算行列式|A|

class Matrix{//矩陣 方陣
public
 
:
    friend void Cal_Astar(Matrix &A);//計算A*
    friend float Cal_Aij(Matrix &A,int i,int j);//計算Aij->A*
    Matrix();
    void Input();
    void Cheak_IsSolvable();
    float CalDet_A();
    void Inverse_of_A();
    void ToAstar(int j,int i,float s){
        Astar[j][i]=s;
    }
    float getAkl(int
 
 k,int l){
        return A[k][l];
    }
    void Dis_A(float s[9][9]);
    void Display(int t);
private:
    int n;              //行，列r=c
    float A[9][9];      //矩陣A
    float Astar[9][9];  // A*
    float Det_A;        // |A|值
    float IOA[9][9];    //inverse of A  A的逆矩陣
};


int main(){
    Matrix A;
    A.Input();
    A.Display(1
 
);       //輸出矩陣A
    A.Cheak_IsSolvable();//檢查是否可解
    Cal_Astar(A);       //計算A*
    A.Inverse_of_A();   //計算A*/|A|
    A.Display(3);       //輸出逆矩陣
    return 1;
}

void Cal_Astar(Matrix &A){
    for(int i=0;i<A.n;i++)
        for(int j=0;j<A.n;j++)
            A.ToAstar(j,i,pow(-1,i+j+2)*Cal_Aij(A,i,j));
        A.Display(2);
}

float Cal_Aij(Matrix &A,int i,int j){
    float Aij[9][9]={0};
    int x=0,y=0;                    //Aij的下標
    for(int k=0;k<A.n;k++){         //k l -> A的下標
        for(int l=0;l<A.n;l++){
            if(k!=i&&l!=j){
                    Aij[x][y]=A.getAkl(k,l);
                    y++;
                    if(!(y%((A.n)-1))){//進位
                        x++;
                        y=0;
                    }
            }
        }
    }
    return Cal_Det(Aij,(A.n)-1);
}

float Cal_Det(float s[9][9],int n){
    float sum=0; //存|A|值
    for(int i=0;i<n-1;i++){
        if(s[i][i]){//對角線元素不為0
            for(int m=i+1;m<n;m++){
                if(s[m][i]){
                    float temp=-(s[m][i])/s[i][i];
                    for(int p=0;p<n;p++)//R(m)+tempRi
                        s[m][p]=s[m][p]+temp*s[i][p];
                }
                else continue;
            }
        }
        else {//若對角線元素為0
            int m;
            for(m=i+1;m<n;m++){//
                if(s[m][i]){//使對角線元素非0
                    for(int p=0;p<n;p++)//Ri+Rm
                        s[i][p]=s[m][p]+s[i][p];
                    break;
                }
                else continue;
            }
            if(m==n) return sum;   //sum=0;
            i--;
        }
    }
    sum=s[0][0];//求對角積
    for(i=1;i<n;i++)
        sum=sum*s[i][i];
    return sum;
}

void Matrix::Dis_A(float s[9][9]){
    for(int i=0;i<n;i++){
        cout<<"|";
        for(int j=0;j<n;j++)
            cout<<setw(8)<<s[i][j];
        cout<<"    |"<<endl;
    }
    cout<<endl;
}
Matrix::Matrix(){
    n=9;
    for(int i=0;i<9;i++)
        for(int j=0;j<9;j++)
            A[i][j]=Astar[i][j]=IOA[i][j]=0;
}
void Matrix::Input(){
    cout<<"\t\t矩陣>>>>>>>>>>>逆矩陣"<<endl<<endl;
    cout<<"方陣A的行列數n:";
    while(1){
        cin>>n;
        if(n>1&&n<10) break;
        else cout<<"n值錯誤，重新輸入：";
    }
    cout<<"矩陣各值:"<<endl;
    for(int i=0;i<n;i++)
        for(int j=0;j<n;j++)
            cin>>A[i][j];
}
void Matrix::Cheak_IsSolvable(){
    while(1){
        if(Det_A=CalDet_A()) break;
        else{
            cout<<"此矩陣的行列式為0，無解"<<endl;
            Input();
        } 
    }
}
float Matrix::CalDet_A(){
    float temp[9][9]={0};
    for(int i=0;i<n;i++)    //臨時賦值
        for(int j=0;j<n;j++)
            temp[i][j]=A[i][j];

        float s=Cal_Det(temp,n);
        cout<<"|A|="<<s<<endl<<endl;
        return s;
}
void Matrix::Inverse_of_A(){
    for(int i=0;i<n;i++)
        for(int j=0;j<n;j++)
            IOA[i][j]=Astar[i][j]/Det_A;
}
void Matrix::Display(int t){
    switch (t){
    case 1: cout<<"---A :"<<endl;Dis_A(A);break;
    case 2: cout<<"---A* :"<<endl;Dis_A(Astar);break;
    case 3: cout<<"---inverse of A :"<<endl;Dis_A(IOA);break;
    }
}