紅黑樹增刪操作的程式碼實現(上)
阿新 • • 發佈:2019-01-31
這幾天一直在學習紅黑樹,由於是第一次接觸,所以剛開始覺得挺麻煩的,經過這幾天的各種google,終於對其的插入和刪除操作有了一定了解,現在就分享下:
紅黑樹的定義:紅黑樹是每個節點都帶有顏色屬性的二叉查詢樹,顏色為紅色或黑色。在二叉查詢樹強制一般要求以外,對於任何有效的紅黑樹我們增加了如下的額外要求:
性質1. 節點是紅色或黑色。
性質2. 根是黑色。
性質3. 所有葉子都是黑色(葉子是NIL節點)。
性質4. 每個紅色節點的兩個子節點都是黑色。(從每個葉子到根的所有路徑上不能有兩個連續的紅色節點。
性質5. 從任一節點到其每個葉子的所有簡單路徑都包含相同數目的黑色節點。
首先是紅黑樹的結構定義:紅黑樹定義為一個擁有5個屬性的結構體:
typedef struct RBTNode{
int color;
struct RBTNode *parent;
struct RBTNode *left;
struct RBTNode *right;
int value;
}RBTNode,*RBTree;在實現紅黑樹的插入操作時,首先要實現樹的旋轉操作,這在插入刪除操作之後調整紅黑樹時要用到,分為左旋和右旋操作,實現程式碼如下:
左旋和右旋操作原理比較簡單,看程式碼就能理解。//右旋操作實現程式碼 void RIGHT_ROTATE(RBTree T,RBTree x) { RBTree y; y = x->left; x->left = y->right; if(y->right!=nil) { y->right->parent = x; } y->parent = x->parent; if(x->parent == nil) { root = y; } else if(x->parent->left == x) { x->parent->left = y; } else { x->parent->right = y; } y->right = x; x->parent = y; } //左旋操作實現程式碼,與右旋操作一樣 void LEFT_ROTATE(RBTree T,RBTree x) { RBTree y; y = x->right; x->right =y->left; if(y->left!=nil) { y->left->parent = x; } y->parent = x->parent; if(x->parent == nil) { root = y; } else if(x == x->parent->left) { x->parent->left = y; } else { x->parent->right = y; } y->left = x; x->parent = y; }
之後是紅黑樹的插入操作,插入操作其實和普通的二叉排序樹的插入操作一樣,只是在插入結點之後,紅黑樹的5條性質可能會被破壞,這樣就需要呼叫調整函式對紅黑樹進行調整,以讓其滿足紅黑樹的5條性質,
紅黑樹的插入實現函式如下:
在將結點插入到紅黑樹的相應位置之後,將新結點塗紅(如果塗黑,就會導致根到葉子的路徑上有一條路上,多了一個額外的黑結點,這個是很難調整的。但塗紅後可能會導致出現兩個連續的紅色結點的衝突,那麼可以通過顏色調整和樹旋轉來調整)。//插入操作,這與一般的二叉排序樹的插入操作類似 void RBTreeInsert(RBTree T,RBTree z) { RBTree x,y; y = nil; x = root; while(x!=nil) { y = x; if(z->value<x->value) { x = x->left; } else { x = x->right; } } z->parent = y; if(y == nil) { root = z; } else if(z->value<y->value) { y->left = z; } else { y->right = z; } z->left = nil; z->right = nil; z->color = RED; RBTreeInsertFixup(T,z); }
插入新結點之後,會出現如下需要調整紅黑樹的情況(還有幾種情況沒列出,因為那些情況不需要調整樹)
1.當紅黑樹中沒有結點時,新結點直接塗黑就可以了。
 2.新結點的父親結點為紅色,並且新結點的叔叔結點也為紅色
2.新結點的父親結點為紅色,並且新結點的叔叔結點也為紅色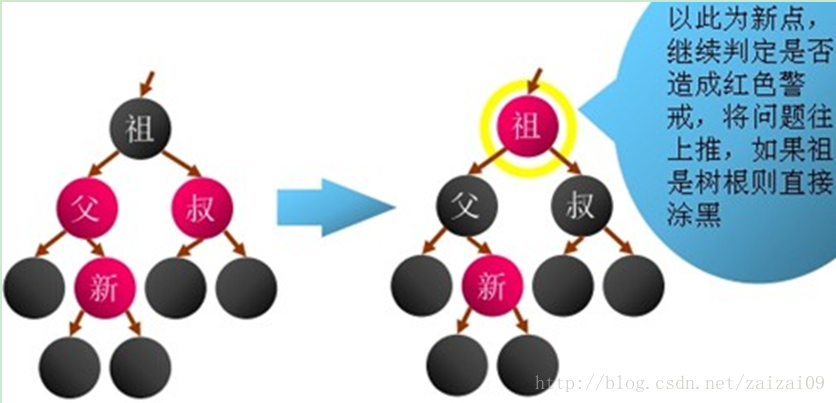
調整方法:父=>黑;叔=>黑;祖=>紅;往上遍歷
3.新結點的父結點為紅色,叔叔結點為黑色,新結點為其父結點的左孩子

調整方法:父=>黑;祖=>紅;祖父右旋轉;
4.新結點的父結點為紅色,叔叔結點為黑色,新結點為其父結點的右孩子
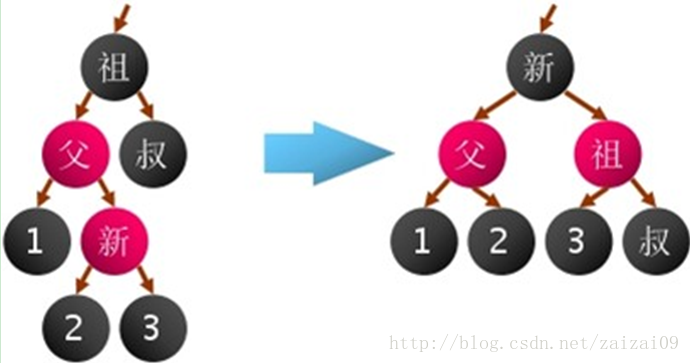
調整方法:新=>黑;祖=>紅;父左旋轉;祖右旋轉
具體的實現程式碼如下所示:
void RBTreeInsertFixup(RBTree T,RBTree z)
{
RBTree y;
while(z->parent->color == RED)//這時說明z肯定存在父結點和祖父結點
{
if(z->parent == z->parent->parent->left)//如果z的父結點為祖父結點的左孩子
{
y = z->parent->parent->right;//y為z的叔叔結點
if(y->color == RED)//情況1:紅叔情況
{//將父結點和叔叔結點塗黑,祖父結點塗紅
z->parent->color = BLACK;
y->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent;//調整之後將祖父結點作為調整物件
}
else
{
if(z == z->parent->right)//z是父結點的右孩子
{//情況2:黑叔,新結點z為右孩子
z = z->parent;
LEFT_ROTATE(T,z);
}
//通過上面兩部操作將情況2轉為情況3,然後兩種情況一起操作
//情況3:黑叔,z為右孩子
z->parent->color = BLACK;
z->parent->parent->color = RED;
RIGHT_ROTATE(T,z->parent->parent);
}
}
else//如果父結點為祖父結點的右孩子
{
y = z->parent->parent->left;//y為z的叔叔結點
if(y->color == RED)//情況1:紅叔
{//將父結點和叔叔結點塗黑,祖父結點塗紅
z->parent->color = BLACK;
y->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent;//調整之後將祖父結點作為調整物件
}
else
{
if(z == z->parent->left)//z為父結點的左孩子
{//情況2:黑叔,新結點為左孩子
z = z->parent;
RIGHT_ROTATE(T,z);
}
//情況3:黑叔,新結點為右孩子
z->parent->color = BLACK;
z->parent->parent->color = RED;
LEFT_ROTATE(T,z->parent->parent);
}
}
}
root->color = BLACK;//包含情況:z為唯一的結點的情況
}