FFT詳解
阿新 • • 發佈:2019-01-31
src sum 表示 strong https 原來 哪裏 lin 情況
二. 點值表示法
眾所周知,兩個點確定一個一次函數,三個點確定一個二次函數。
所以,\(n+1\)個點確定一個一元\(n\)次多項式。
所以我們可以通過\(n+1\)個點來表示它。
那麽相乘之後的點值如何計算?
比如說兩個2次多項式\(F(x)=x^2+2x+1\)(紅色)與\(G(x)=3x^2-4x-2\)(藍色),它們的圖像如圖所示:
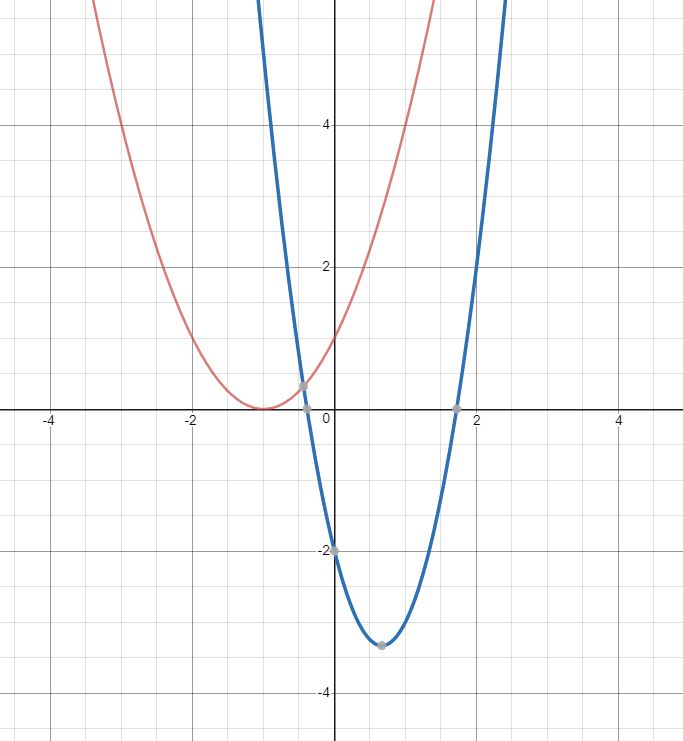
那麽觀察圖中\(x=1\)時的情況。此時\(F(1)=4,G(1)=-3.\)
所以,顯然,\(F(1)\times G(1)=-12\).也就是說在\(Z=F*G\)這一多項式內,帶入\(1\),得到的結果是\(-12\)
等等,好像有哪裏不對。如果說\(Z=F*G\)的話,那麽Z的次數應該是\(2n\).
那\(Z\)需要\(2n+1\)個點來確定。但是原來只需要\(n+1\)個點,咋辦?
很簡單,在原來的多項式裏每個都多加\(n\)個點即可。反正多項式已知。
這樣就可以用點值來進行操作。也就是說先轉成點值,再一乘,再轉回來,就是計算流程。
但是好像還是很慢。那麽如何優化呢?
復數部分
復數,即形如\(a+bi\)的數,其中\(\sqrt{i}=-1.\) \(a\)稱為實部,\(bi\)稱為虛部。
或者說:在一個數軸上(只有x軸),我們可以表示出任何實數。
那麽,多加一維(y軸),也就是類似於平面直角坐標系一樣,我們就可以表示出任意一個復數。
所以我們把這個坐標系叫做復平面
復數運算
復數相加:實部相加,虛部相加,例如
\[(a+bi)+(c+di)=(a+c)+(b+d)i.\]
復數相減:同理。
\[(a+bi)-(c+di)=(a-c)+(b-d)i.\]
復數相乘:像一次多項式一樣相乘。 註意\(i^2=-1\).
\[(a+bi)(c+di)=ac+(ad+bc)i-bd=(ac-bd)+(ad+bc)i.\]
復數相除:
相信大家都學過共軛根式。同樣的,復數也有共軛。
即:\(a+bi\)的共軛為\(a-bi\)。
這兩個復數卡乘在一起一定是個實數。即
\[(a+bi)(a-bi)=a^2-(bi)^2=a^2+b^2.\]
所以再除的時候,將分子分母同乘分母的共軛,就可以將分母有理化。
即
\[\frac{a+bi}{c+di}=\frac{(a+bi)(c-di)}{c^2+d^2}=\frac{(ac+bd)}{c^2+d^2}+\frac{bc-ad}{c^2+d^2}i.\]
復數逆元:
\[\frac{1}{a+bi}=\frac{a}{a^2+b^2}-\frac{b}{a^2+b^2}i.\]
快速傅裏葉變換\(\text{(FFT)}\)
筆者學習的是這份博客
內容中可能有很多相同之處,敬請諒解。
現在要計算兩個一元\(n\)次多項式\(F(x)\)與\(G(x)\)的乘積,如何計算?
前置知識:多項式的表示方法
一. 系數表示法
對於一個\(n\)次多項式\(F(x)\),它可以被表示成
\[F(x) = a_nx^n+a_{n-1}x^{n-1}+...+a_1x^1+a_0x^0.\]
更加形式化的來說,它可以表示成
\[F(x) = \sum_{i=0}^{n} a_ix^i.\]
舉個例子,2次多項式,其中\(a_0=1,a_1=2,a_2=1\)
那麽\(F(x)=1x^2+2x+1.\)
二. 點值表示法
所以,\(n+1\)個點確定一個一元\(n\)次多項式。
所以我們可以通過\(n+1\)個點來表示它。
那麽相乘之後的點值如何計算?
比如說兩個2次多項式\(F(x)=x^2+2x+1\)(紅色)與\(G(x)=3x^2-4x-2\)(藍色),它們的圖像如圖所示:

那麽觀察圖中\(x=1\)時的情況。此時\(F(1)=4,G(1)=-3.\)
所以,顯然,\(F(1)\times G(1)=-12\).也就是說在\(Z=F*G\)這一多項式內,帶入\(1\),得到的結果是\(-12\)
等等,好像有哪裏不對。如果說\(Z=F*G\)的話,那麽Z的次數應該是\(2n\).
那\(Z\)需要\(2n+1\)個點來確定。但是原來只需要\(n+1\)個點,咋辦?
很簡單,在原來的多項式裏每個都多加\(n\)個點即可。反正多項式已知。
這樣就可以用點值來進行操作。也就是說先轉成點值,再一乘,再轉回來,就是計算流程。
但是好像還是很慢。那麽如何優化呢?
復數部分
復數,即形如\(a+bi\)的數,其中\(\sqrt{i}=-1.\) \(a\)稱為實部,\(bi\)稱為虛部。
或者說:在一個數軸上(只有x軸),我們可以表示出任何實數。
那麽,多加一維(y軸),也就是類似於平面直角坐標系一樣,我們就可以表示出任意一個復數。
所以我們把這個坐標系叫做復平面
復數運算
復數相加:實部相加,虛部相加,例如
\[(a+bi)+(c+di)=(a+c)+(b+d)i.\]
復數相減:同理。
\[(a+bi)-(c+di)=(a-c)+(b-d)i.\]
復數相乘:像一次多項式一樣相乘。 註意\(i^2=-1\).
\[(a+bi)(c+di)=ac+(ad+bc)i-bd=(ac-bd)+(ad+bc)i.\]
復數相除:
相信大家都學過共軛根式。同樣的,復數也有共軛。
即:\(a+bi\)的共軛為\(a-bi\)。
這兩個復數
\[(a+bi)(a-bi)=a^2-(bi)^2=a^2+b^2.\]
所以再除的時候,將分子分母同乘分母的共軛,就可以將分母有理化。
即
\[\frac{a+bi}{c+di}=\frac{(a+bi)(c-di)}{c^2+d^2}=\frac{(ac+bd)}{c^2+d^2}+\frac{bc-ad}{c^2+d^2}i.\]
復數逆元:
\[\frac{1}{a+bi}=\frac{a}{a^2+b^2}-\frac{b}{a^2+b^2}i.\]
FFT詳解
