快速傅立葉變換(FFT)詳解
本文只討論FFT在資訊學奧賽中的應用
文中內容均為個人理解,如有錯誤請指出,不勝感激
前言
先解釋幾個比較容易混淆的縮寫吧
DFT:離散傅立葉變換—>$O(n^2)$計算多項式乘法
FFT:快速傅立葉變換—>$O(n*\log(n)$計算多項式乘法
FNTT/NTT:快速傅立葉變換的優化版—>優化常數及誤差
FWT:快速沃爾什變換—>利用類似FFT的東西解決一類卷積問題
MTT:毛爺爺的FFT—>非常nb/任意模數
FMT 快速莫比烏斯變化—>感謝stump提供
多項式
係數表示法
設$A(x)$表示一個$n-1$次多項式
則$A(x)=\sum_{i=0}^{n} a_i * x^i$
例如:$A(3)=2+3*x+x^2$
利用這種方法計算多項式乘法複雜度為$O(n^2)$
(第一個多項式中每個係數都需要與第二個多項式的每個係數相乘)
點值表示法
將$n$互不相同的$x$帶入多項式,會得到$n$個不同的取值$y$
則該多項式被這$n$個點$(x_1,y_1),(x_2,y_2),\dots,(x_n,y_n)$唯一確定
其中$y_i=\sum_{j=0}^{n-1} a_j*x_i^j$
例如:上面的例子用點值表示法可以為$(0,2),(1,6),(2,12)$
利用這種方法計算多項式乘法的時間複雜度仍然為$O(n^2)$
(選點$O(n)$,每次計算$O(n)$)
我們可以看到,兩種方法的時間複雜度都為$O(n^2)$,我們考慮對其進行優化
對於第一種方法,由於每個點的係數都是固定的,想要優化比較困難
對於第二種方法,貌似也沒有什麼好的優化方法,不過當你看完下面的知識,或許就不這麼想了
複數
在介紹複數之前,首先介紹一些可能會用到的東西
向量
同時具有大小和方向的量
在幾何中通常用帶有箭頭的線段表示
圓的弧度制
等於半徑長的圓弧所對的圓心角叫做1弧度的角,用符號rad表示,讀作弧度。用弧度作單位來度量角的制度叫做弧度制
公式:
$1^{\circ }=\dfrac{\pi}{180}rad$
$180^{\circ }=\pi rad$
平行四邊形定則
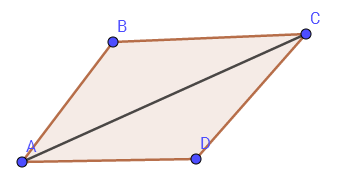
(好像畫的不是很標準。。)
平行四邊形定則:AB+AD=AC
複數
定義
設$a,b$為實數,$i^2=-1$,形如$a+bi$的數叫複數,其中$i$被稱為虛數單位,複數域是目前已知最大的域
在複平面中,$x$代表實數,$y$軸(除原點外的點)代表虛數,從原點$(0,0)$到$(a,b)$的向量表示複數$a+bi$
模長:從原點$(0,0)$到點$(a,b)$的距離,即$\sqrt{a^2+b^2}$
幅角:假設以逆時針為正方向,從$x$軸正半軸到已知向量的轉角的有向角叫做幅角
運演算法則
加法:
因為在複平面中,複數可以被表示為向量,因此複數的加法與向量的加法相同,都滿足平行四邊形定則(就是上面那個)
乘法:
幾何定義:複數相乘,模長相乘,幅角相加
代數定義:$$(a+bi)*(c+di)$$
$$=ac+adi+bci+bdi^2$$
$$=ac+adi+bci-bd$$
$$=(ac-bd)+(bc+ad)i$$
單位根
下文中,預設$n$為$2$的正整數次冪
在複平面上,以原點為圓心,$1$為半徑作圓,所得的圓叫單位圓。以圓點為起點,圓的$n$等分點為終點,做$n$個向量,設幅角為正且最小的向量對應的複數為$\omega_n$,稱為$n$次單位根。
根據複數乘法的運演算法則,其餘$n-1$個複數為$\omega_n^2,\omega_n^3,\ldots,\omega_n^n$
注意$\omega_n^0=\omega_n^n=1$(對應複平面上以$x$軸為正方向的向量)
那麼如何計算它們的值呢?這個問題可以由尤拉公式解決$$\omega_{n}^{k}=\cos\ k *\frac{2\pi}{n}+i\sin k*\frac{2\pi}{n}$$
例如
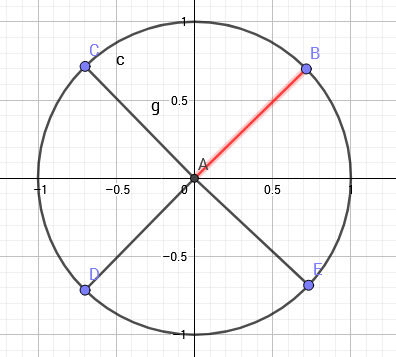
圖中向量$AB$表示的複數為$8$次單位根
單位根的幅角為周角的$\frac{1}{n}$
在代數中,若$z^n=1$,我們把$z$稱為$n$次單位根
單位根的性質
- $\omega _{n}^{k}=\cos k\dfrac{2\pi}{n}+i\sin k\dfrac {2\pi }{n}$(即上面的公式)
- $\omega _{2n}^{2k}=\omega _{n}^{k}$
證明:
$$\omega _{2n}^{2k}=\cos 2k*\frac{2\pi}{2n}+i\sin2k*\frac{2\pi}{2n}$$
$$=\omega _{n}^{k}$$
- $\omega _{n}^{k+\frac{n}{2}}=-\omega _{n}^{k}$
$$\omega _{n}^{\frac{n}{2}}=\cos\frac{n}{2}*\frac{2\pi}{n}+i\sin\frac{n}{2}*\frac{2\pi}{n}$$
$$=\cos \pi+i\sin\pi$$
$$=-1$$
- $\omega _{n}^{0}=\omega _{n}^{n}=1$
講了這麼多,貌似跟我們的正題沒啥關係啊。。
OK!各位坐穩了,前方高能!
快速傅立葉變換
我們前面提到過,一個$n$次多項式可以被$n$個點唯一確定。
那麼我們可以把單位根的$0$到$n-1$次冪帶入,這樣也可以把這個多項式確定出來。但是這樣仍然是$O(n^2)$的呀!
我們設多項式$A(x)$的係數為$(a_o,a_1,a_2,\ldots,a_{n-1})$
那麼$$A(x)=a_0+a_1*x+a_2*{x^2}+a_3*{x^3}+a_4*{x^4}+a_5*{x^5}+ \dots+a_{n-2}*x^{n-2}+a_{n-1}*x^{n-1}$$
將其下標按照奇偶性分類
$$A(x)=(a_0+a_2*{x^2}+a_4*{x^4}+\dots+a_{n-2}*x^{n-2})+(a_1*x+a_3*{x^3}+a_5*{x^5}+ \dots+a_{n-1}*x^{n-1})$$
設
$$A_1(x)=a_0+a_2*{x}+a_4*{x^2}+\dots+a_{n-2}*x^{\frac{n}{2}-1}$$
$$A_2(x)=a_1+a_3*{x}+a_5*{x^2}+ \dots+a_{n-1}*x^{\frac{n}{2}-1}$$
那麼不難得到
$$A(x)=A_1(x^2)+xA_2(x^2)$$
我們將$\omega_n^k (k<\frac{n}{2}) $代入得
$$A(\omega_n^k)=A_1(\omega_n^{2k})+\omega_n^kA_2(\omega_n^{2k})$$
$$=A_1(\omega_{\frac{n}{2}}^{k})+\omega_n^kA_2(\omega_{\frac{n}{2}}^{k})$$
同理,將$\omega_n^{k+\frac{n}{2}}$代入得
$$A(\omega_n^{k+\frac{n}{2}})=A_1(\omega_n^{2k+n})+\omega_n^{k+\frac{n}{2}}(\omega_n^{2k+n})$$
$$=A_1(\omega_n^{2k}*\omega_n^n)-\omega_n^kA_2(\omega_n^{2k}*\omega_n^n)$$
$$=A_1(\omega_n^{2k})-\omega_n^kA_2(\omega_n^{2k})$$
大家有沒有發現什麼規律?
沒錯!這兩個式子只有一個常數項不同!
那麼當我們在列舉第一個式子的時候,我們可以$O(1)$的得到第二個式子的值
又因為第一個式子的$k$在取遍$[0,\frac{n}{2}-1]$時,$k+\frac{n}{2}$取遍了$[\frac{n}{2},n-1]$
所以我們將原來的問題縮小了一半!
而縮小後的問題仍然滿足原問題的性質,所以我們可以遞迴的去搞這件事情!
直到多項式僅剩一個常數項,這時候我們直接返回就好啦
時間複雜度:
不難看出FFT是類似於線段樹一樣的分治演算法。
因此它的時間複雜度為$O(nlogn)$
快速傅立葉逆變換
不要以為FFT到這裡就結束了。
我們上面的討論是基於點值表示法的。
但是在平常的學習和研究中很少用點值表示法來表示一個多項式。
所以我們要考慮如何把點值表示法轉換為係數表示法,這個過程叫做傅立葉逆變換
$(y_0,y_1,y_2,\dots,y_{n-1})$為$(a_0,a_1,a_2,\dots,a_{n-1})$的傅立葉變換(即點值表示)
設有另一個向量$(c_0,c_1,c_2,\dots,c_{n-1})$滿足
$$c_k=\sum_{i=0}^{n-1}y_i(\omega_n^{-k})^i$$
即多項式$B(x)=y_0,y_1x,y_2x^2,\dots,y_{n-1}x^{n-1}$在$\omega_n^{0},\omega_n^{-1},\omega_n^{-2},\dots,\omega_{n-1}^{-(n-1)}$處的點值表示
emmmm又到推公式時間啦
$(c_0,c_1,c_2,\dots,c_{n-1})$滿足
$$c_k=\sum_{i=0}^{n-1}y_i(\omega_n^{-k})^i$$
$$=\sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}a_j(\omega_n^i)^j)(\omega_n^{-k})^i$$
$$=\sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}a_j(\omega_n^j)^i)(\omega_n^{-k})^i$$
$$=\sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}a_j(\omega_n^j)^i(\omega_n^{-k})^i)$$
$$=\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}a_j(\omega_n^j)^i(\omega_n^{-k})^i$$
$$=\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}a_j(\omega_n^{j-k})^i$$
$$=\sum_{j=0}^{n-1}a_j(\sum_{i=0}^{n-1}(\omega_n^{j-k})^i)$$
設$S(x)=\sum_{i=0}^{n-1}x^i$
將$\omega_n^k$代入得
$$S(\omega_n^k)=1+(\omega_n^k)+(\omega_n^k)^2+\dots(\omega_n^k)^{n-1}$$
當$k!=0$時
等式兩邊同乘$\omega_n^k$得
$$\omega_n^kS(\omega_n^k)=\omega_n^k+(\omega_n^k)^2+(\omega_n^k)^3+\dots(\omega_n^k)^{n}$$
兩式相減得
$$\omega_n^kS(\omega_n^k)-S(\omega_n^k)=(\omega_n^k)^{n}-1$$
$$S(\omega_n^k)=\frac{(\omega_n^k)^{n}-1}{\omega_n^k-1}$$
$$S(\omega_n^k)=\frac{(\omega_n^n)^{k}-1}{\omega_n^k-1}$$
$$S(\omega_n^k)=\frac{1-1}{\omega_n^k-1}$$
觀察這個式子,不難看出它分母不為0,但是分子為0
因此,當$K!=0$時,$S(\omega^{k}_{n})=0$
那當$k=0$時呢?
很顯然,$S(\omega^{0}_{n})=n$
繼續考慮剛剛的式子
$$c_k=\sum_{j=0}^{n-1}a_j(\sum_{i=0}^{n-1}(\omega_n^{j-k})^i)$$
當$j \neq k$時,值為$0$
當$j=k$時,值為$n$
因此,
$$c_k=na_k$$
$$a_k=\frac{c_k}{n}$$
這樣我們就得到點值與係數之間的表示啦
理論總結
至此,FFT的基礎理論部分就結束了。
我們來小結一下FFT是怎麼成功實現的
首先,人們在用係數表示法研究多項式的時候遇阻
於是開始考慮能否用點值表示法優化這個東西。
然後根據複數的兩條性質(這個思維跨度比較大)得到了一種分治演算法。
最後又推了一波公式,找到了點值表示法與係數表示法之間轉換關係。
emmmm
其實FFT的實現思路大概就是
係數表示法—>點值表示法—>係數表示法
引用一下遠航之曲大佬的圖
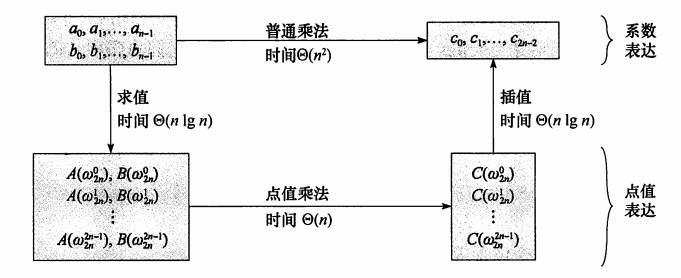
當然,在實現的過程中還有很多技巧
我們根據程式碼來理解一下
遞迴實現
遞迴實現的方法比較簡單。
就是按找我們上面說的過程,不斷把要求的序列分成兩部分,再進行合併
在c++的STL中提供了現成的complex類,但是我不建議大家用,畢竟手寫也就那麼幾行,而且萬一某個毒瘤卡STL那豈不是很GG?
#include<iostream> #include<cstdio> #include<cmath> using namespace std; const int MAXN=2*1e6+10; inline int read() { char c=getchar();int x=0,f=1; while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } const double Pi=acos(-1.0); struct complex { double x,y; complex (double xx=0,double yy=0){x=xx,y=yy;} }a[MAXN],b[MAXN]; complex operator + (complex a,complex b){ return complex(a.x+b.x , a.y+b.y);} complex operator - (complex a,complex b){ return complex(a.x-b.x , a.y-b.y);} complex operator * (complex a,complex b){ return complex(a.x*b.x-a.y*b.y , a.x*b.y+a.y*b.x);}//不懂的看複數的運算那部分 void fast_fast_tle(int limit,complex *a,int type) { if(limit==1) return ;//只有一個常數項 complex a1[limit>>1],a2[limit>>1]; for(int i=0;i<=limit;i+=2)//根據下標的奇偶性分類 a1[i>>1]=a[i],a2[i>>1]=a[i+1]; fast_fast_tle(limit>>1,a1,type); fast_fast_tle(limit>>1,a2,type); complex Wn=complex(cos(2.0*Pi/limit) , type*sin(2.0*Pi/limit)),w=complex(1,0); //Wn為單位根,w表示冪 for(int i=0;i<(limit>>1);i++,w=w*Wn)//這裡的w相當於公式中的k a[i]=a1[i]+w*a2[i], a[i+(limit>>1)]=a1[i]-w*a2[i];//利用單位根的性質,O(1)得到另一部分 } int main() { int N=read(),M=read(); for(int i=0;i<=N;i++) a[i].x=read(); for(int i=0;i<=M;i++) b[i].x=read(); int limit=1;while(limit<=N+M) limit<<=1; fast_fast_tle(limit,a,1); fast_fast_tle(limit,b,1); //後面的1表示要進行的變換是什麼型別 //1表示從係數變為點值 //-1表示從點值變為係數 //至於為什麼這樣是對的,可以參考一下c向量的推導過程, for(int i=0;i<=limit;i++) a[i]=a[i]*b[i]; fast_fast_tle(limit,a,-1); for(int i=0;i<=N+M;i++) printf("%d ",(int)(a[i].x/limit+0.5));//按照我們推倒的公式,這裡還要除以n return 0; }
這裡還有一個聽起來很裝B的優化—蝴蝶操作
觀察合併的過程,w*a2[i] 這一項計算了兩次,因為理論上來說複數的乘法是比較慢的,所以我們可以把這一項記出來
此處我犯了一個概念性的錯誤,蝴蝶操作應當是下面的“迭代實現”。。
for(int i=0;i<(limit>>1);i++,w=w*Wn)//這裡的w相當於公式中的k
{
complex t=w*a2[i];//蝴蝶操作
a[i]=a1[i]+t,
a[i+(limit>>1)]=a1[i]-t;//利用單位根的性質,O(1)得到另一部分
}

woc? 臉好疼。。。。。。
咳咳。
速度什麼的才不是關鍵呢?
關鍵是我們AC不了啊啊啊
表著急,AC不了不代表咱們的演算法不對,只能說這種實現方法太low了
下面介紹一種更高效的方法
迭代實現
再盜一下那位大佬的圖

觀察一下原序列和反轉後的序列?
聰明的你有沒有看出什麼顯而易見的性質?
沒錯!
我們需要求的序列實際是原序列下標的二進位制反轉!
因此我們對序列按照下標的奇偶性分類的過程其實是沒有必要的
這樣我們可以$O(n)$的利用某種操作得到我們要求的序列,然後不斷向上合併就好了
// luogu-judger-enable-o2 #include<iostream> #include<cstdio> #include<cmath> using namespace std; const int MAXN=1e7+10; inline int read() { char c=getchar();int x=0,f=1; while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } const double Pi=acos(-1.0); struct complex { double x,y; complex (double xx=0,double yy=0){x=xx,y=yy;} }a[MAXN],b[MAXN]; complex operator + (complex a,complex b){ return complex(a.x+b.x , a.y+b.y);} complex operator - (complex a,complex b){ return complex(a.x-b.x , a.y-b.y);} complex operator * (complex a,complex b){ return complex(a.x*b.x-a.y*b.y , a.x*b.y+a.y*b.x);}//不懂的看複數的運算那部分 int N,M; int l,r[MAXN]; int limit=1; void fast_fast_tle(complex *A,int type) { for(int i=0;i<limit;i++) if(i<r[i]) swap(A[i],A[r[i]]);//求出要迭代的序列 for(int mid=1;mid<limit;mid<<=1)//待合併區間的長度的一半 { complex Wn( cos(Pi/mid) , type*sin(Pi/mid) ); //單位根 for(int R=mid<<1,j=0;j<limit;j+=R)//R是區間的長度,j表示前已經到哪個位置了 { complex w(1,0);//冪 for(int k=0;k<mid;k++,w=w*Wn)//列舉左半部分 { complex x=A[j+k],y=w*A[j+mid+k];//蝴蝶效應 A[j+k]=x+y; A[j+mid+k]=x-y; } } } } int main() { int N=read(),M=read(); for(int i=0;i<=N;i++) a[i].x=read(); for(int i=0;i<=M;i++) b[i].x=read(); while(limit<=N+M) limit<<=1,l++; for(int i=0;i<limit;i++) r[i]= ( r[i>>1]>>1 )| ( (i&1)<<(l-1) ) ; // 在原序列中 i 與 i/2 的關係是 : i可以看做是i/2的二進位制上的每一位左移一位得來 // 那麼在反轉後的陣列中就需要右移一位,同時特殊處理一下奇數 fast_fast_tle(a,1); fast_fast_tle(b,1); for(int i=0;i<=limit;i++) a[i]=a[i]*b[i]; fast_fast_tle(a,-1); for(int i=0;i<=N+M;i++) printf("%d ",(int)(a[i].x/limit+0.5)); return 0; }
相關推薦
快速傅立葉變換(FFT)詳解
本文只討論FFT在資訊學奧賽中的應用 文中內容均為個人理解,如有錯誤請指出,不勝感激 前言 先解釋幾個比較容易混淆的縮寫吧 DFT:離散傅立葉變換—>$O(n^2)$計算多項式乘法 FFT:快速傅立葉變換—>$O(n*\log(n)$計算多項式乘法 FNTT/NTT:快速傅立葉變換的優
快速傅立葉變換FFT模板
return namespace double names http ++ main swap pre 遞歸版 UOJ34多項式乘法 //容易暴棧,但是很好理解 #include <cmath> #include <iostream> #includ
快速傅立葉變換FFT的學習筆記一:C語言程式碼的簡單實現
快速傅立葉變換FFT的學習筆記一:C語言程式碼的簡單實現 fft.c #include "math.h" #include "fft.h" void conjugate_complex(int n,complex in[],complex out[]) { int i = 0
快速傅立葉變換FFT(模板)
轉載出處 https://blog.csdn.net/f_zyj/article/details/76037583 摘自大佬的部落格 FFT(最詳細最通俗的入門手冊) const double PI=acos(-1.0); // 複數結構體 struct Complex { dou
基於python的快速傅立葉變換FFT(二)
基於python的快速傅立葉變換FFT(二)本文在上一篇部落格的基礎上進一步探究正弦函式及其FFT變換。 知識點 FFT變換,其實就是快速離散傅立葉變換,傅立葉變換是數字訊號處理領域一種很重要的演算法。要知道傅立葉變換演算法的意義,首先要了解傅立葉原理的意義。傅立葉原理表明:任何連續測量的時序或訊號,都可
快速傅立葉變換FFT的學習筆記二:深入實踐
快速傅立葉變換FFT的學習筆記二:深入實踐 快速傅立葉變換(Fast Fourier Transform)是離散傅立葉變換的一種快速演算法,簡稱FFT,通過FFT可以將一個訊號從時域變換到頻域。 資料結構 通過AD採集到一串時域上的資料點,一個int型的陣列
快速傅立葉變換(FFT)學習筆記
快速傅立葉變換(FFT)學習筆記 快速傅立葉變換(\(\rm Fast\ Fourier\ Transformation\)), 用於在 \(\Theta(n\log n)\) 時間內求兩個多項式的乘積. 前置技能 卷積 一個 \(n - 1\) 次 \(n\) 項式 \(f(x)\) 可以表示為 \
[模板]快速傅立葉變換 FFT
#include <iostream> #include <cstdio> #include <cstring> #include <cmath> using namespace std; #define reg register inline
opencv 中 快速傅立葉變換 FFT
opencv 中 傅立葉變換 FFT,程式碼如下: void fft2(IplImage *src, IplImage *dst) { //實部、虛部 IplImage *image_Re = 0, *image_Im = 0, *Fourier = 0; //
快速傅立葉變換FFT總結
快速傅立葉變換,在競賽中離散傅立葉變換DFT及其逆變換IDFT尤為常用,主要用於快速求多項式的乘積。形式化地說,多項式就是某個f(x)=∑i=0naixi,兩個係數分別為ai和bi,那麼(f×g)(x)=f(x)g(x)=∑i=0n∑j=0naibjxi+j,容
Algorithm: 多項式乘法 Polynomial Multiplication: 快速傅立葉變換 FFT / 快速數論變換 NTT
Intro: 本篇部落格將會從樸素乘法講起,經過分治乘法,到達FFT和NTT 旨在能夠讓讀者(也讓自己)充分理解其思想 模板題入口:洛谷 P3803 【模板】多項式乘法(FFT) 樸素乘法 約定:兩個多項式為\(A(x)=\sum_{i=0}^{n}a_ix^i,B(x)=\sum_{i=0}^{m}b_i
快速傅立葉變換(FFT)及其應用
有一個 swap max read mes turn scan 原本 color 在信息學競賽中FFT只有一個用處那就是加速多項式的乘法 多項式乘法原本的時間復雜度是O(n^2)的,然後經過FFT之後可以優化為O(nlogn) FFT就是將系數表示法轉化成點值表示法相乘,再
離散傅立葉變換(DFT)和快速傅立葉變換(FFT)原理與實現
目錄 1、影象變換 2、離散傅立葉變換(Discrete Fourier Transform) 3、DFT性質 4、DFT與數字影象處理 5、FFT-快速傅立葉變換 6、DFT與FFT的演算法實現 1. 影象變換 — —數學領域中有很多種變換,如傅立葉變換、拉普拉斯變
FFT(快速傅立葉變換)
- 概念引入 - 點值表示 對於一個$n - 1$次多項式$A(x)$,可以通過確定$n$個點與值(即$x$和$y$)來表示這唯一的$A(x)$ - 複數 對於一元二次方程 $$x^2 + 1 = 0$$ 在實數範圍內無解,那麼我們將實數範圍擴充,就得到了複數,
【知識總結】快速傅立葉變換(FFT)
這可能是我第五次學FFT了……菜哭qwq 先給出一些個人認為非常優秀的參考資料: 一小時學會快速傅立葉變換(Fast Fourier Transform) - 知乎 小學生都能看懂的FFT!!! - 胡小兔 - 部落格園 快速傅立葉變換(FFT)用於計算兩個\(n\)次多項式相乘,能把複雜度從樸素的\
[學習筆記]FFT——快速傅立葉變換
大力推薦部落格: 傅立葉變換(FFT)學習筆記 一、多項式乘法: 我們要明白的是:FFT利用分治,處理多項式乘法,達到O(nlogn)的複雜度。(雖然常數大)FFT=DFT+IDFTDFT:本質是把多項式的係數表達轉化為點值表達。因為點值表達,y可以直接相乘。點值表達下相
5.6.1 快速傅立葉變換(FFT+RFFT)
1.影象頻域處理的意義 在影象處理和分析中,經常會將影象從影象空間轉換到其他空間中,並利用這些空間的特點進行對轉換後圖像進行分析處理,然後再將處理後的影象轉換到影象空間中,這稱之為影象變換。 在一些影象處理和分析中通過空間變換往往會取得更有效
快速傅立葉變換(FFT)(學習筆記)
學習了一波 F F T FFT
[FFT] 快速傅立葉變換學習筆記
原文:https://blog.csdn.net/herano/article/details/71213373 -1、為什麼學 FFT 退役(很早)之前聽說 FFT 很神(e)奇(xin),Po姐來講的時候也是膜(sha)了(ye)一(bu)發(dong),於是就放那裡了。退役之後有(
快速傅立葉變換(Fast-Fourier Transform,FFT)
數學定義: (詳細參考:https://www.baidu.com/link?url=oYAuG2o-pia_U3DlF5n_MJZyE5YKfaVRUHTTDbM1FwM_kDTjGCxKpw_PbOK70jE2geVioprSVyPTTQuLwN-IhMH8NREmWSDnmcfQEY8w0kq&
