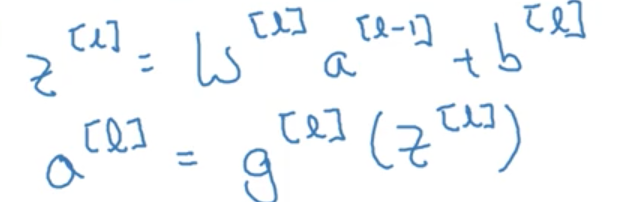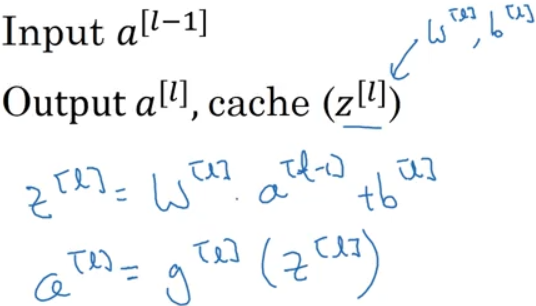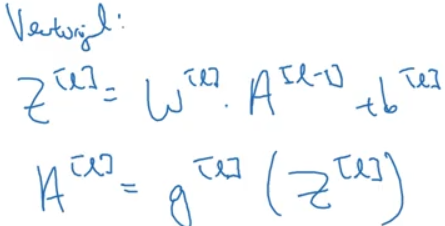Neural Networks and Deep Learning 第四周
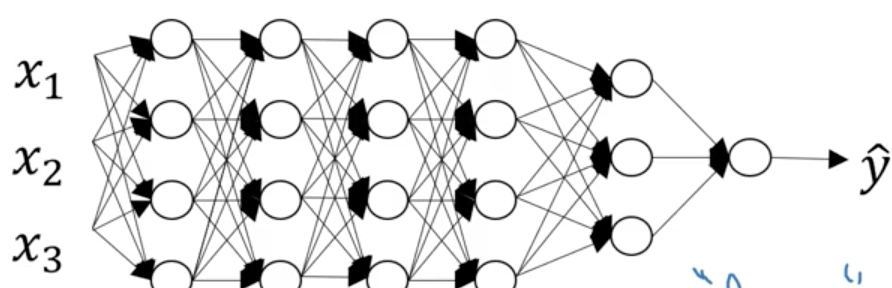
什麼是深度神經網路
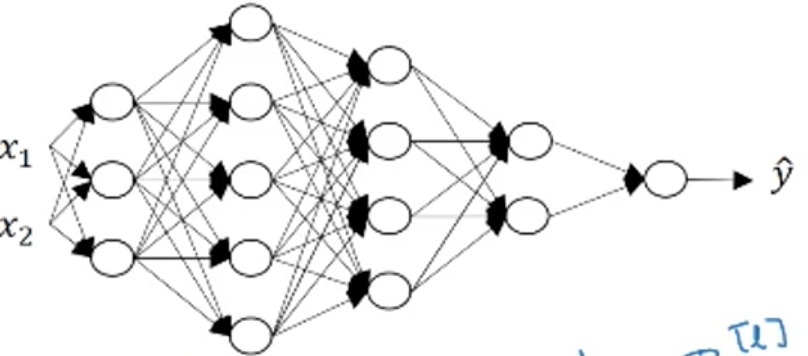
神經網路的個數是隱藏層+輸出層,輸入層不計入。
符號表示:
L代表神經網路的個數,上面按個就有6層神經網路,所以L=6。
n^[l]代表在第l層神經網路中,有多少神經元個數。注意,輸入層是n[0]=nx
a[l]代表在第l層神經網路中,所使用的啟用函式。
w[l]代表在第l層神經網路中,計算中間函式z時所使用的權重。b是偏置。
在深度神經網路中的前向傳播(forward propagation)
對於每一層單一的前向傳播,有一個通用公式:
那麼,對於每一層那麼多個神經元的前線傳播,有沒有一個向量化的表達方式呢?
這是課時的例子,為了很好地理解矩陣變換,我寫的更加透徹一些。
假如第一層n[1] = 4, 那麼,就有四個神經元,每個神經元的W不同,b不同,傳入a[0]後,第一個神經元的結果是z[1][1],第二個是z[1][2],第三個是z[1][3],第四個是z[1][4],那麼,將他們水平排列,得到一個大寫的Z,大寫Z的維度是(1,n0)(n0是前一層神經元的個數,因為你要給每一個都配引數w,所以w.dot(x)中,w是(1,nx),b是(1,n0);那麼,A[1]也就是相同的維度,每個神經元是列向量,將每個神經元橫向排列;資料以(1,n1)的維度傳入L[2];
在深度學習中得到正確的維度

x1,x2是矩陣的特徵數,是2;那麼,每層的神經元就是特徵,比如,第一層有三個神經元,就是三個特徵;當有m個樣本時,也就是X = [[x11,x21],[x12,x22]],這裡的特徵是縱向的,因為每個樣本是列向量,那麼樣本之間就是橫向堆疊;好了,那麼,假設有三個樣本,那麼,X = (2,3) 2是特徵數,x1,x2,3是樣本數,每個樣本都有x1,x2;
好了,樣本傳到了第二層,X = (2,3),由WX可知道,W的列一定是=2的,所以w=(n[l], n[l-1]);點乘之後,wx = (n[l], 3);b由於廣播效應,(n[l],1) 會應用在z的每一列,變成(n[l],3);那麼,Z就是(n[l],3)了。所以,z,a都會由於樣本個數的變化而變化。
Why deep representations?
為什麼需要deep learning?也就是deep learning存在性的問題。為什麼不做一個單層的訓練模型就可以了?有幾個例子:
- 影象識別
影象識別的思路很有意思。layer 1是檢測出圖片的邊緣,然後layer 2將這些邊緣組合起來,組成人臉的區域性的特徵;layer 3把他們都組合起來,變成一張張人臉。那麼,如果裡面多加一層,比如加在layer 2之後,是將區域性特徵組合成一半的臉的特徵,這樣複雜度會減少,並且準確率也會變高。 - 語音識別
淺層的神經元能夠檢測一些簡單的音調,然後較深的神經元能夠檢測出基本的音素,更深的神經元就能夠檢測出單詞資訊。神經網路從左到右,神經元提取的特徵從簡單到複雜。特徵複雜度與神經網路層數成正相關。特徵越來越複雜,功能也越來越強大。 - 減少神經元個數,減少計算量
對於n個樣本,如果你僅僅用一層,也就是輸出層來訓練,那麼,神經元個數是指數型增長 n^[L] = 2^(n-1)。
使用電路理論,對於這個邏輯運算,如果使用深度網路,深度網路的結構是每層將前一層的兩兩單元進行異或,最後到一個輸出。這樣,整個深度網路的層數是log2(n),不包含輸入層。總共使用的神經元個數為n-1個。 - 不好懂,原理其實就是神經網路的個數和處理樣本的邏輯有關係,也和減少神經元個數有關係。
Building blocks of deep neural networks
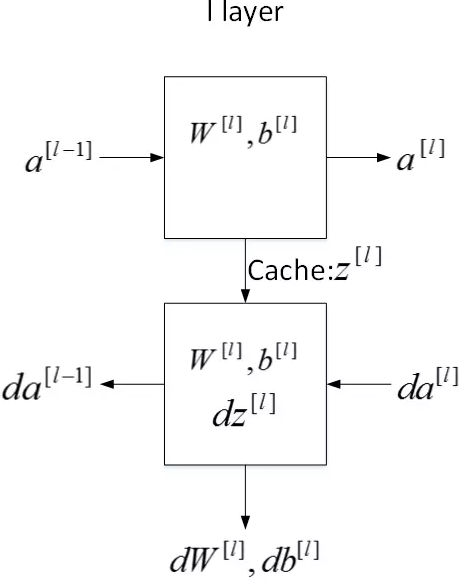
每一層的正向傳播和反向傳播。
Forward and Backward Propagation
首先回顧下正向傳播的流程:
對於L層,輸入是L-1層啟用函式的輸出值a[L-1];輸出是L層的啟用函式的輸出值a[L];並且將該層Z[L],W[L],b[L]的值存入變數中。在該層中,Z[L] = W[L].dot(a[L]) +b[L],每一個a[L-1]層中的神經元都給了不同的權重並輸出;然後輸出結果再用L層的啟用函式計算。
向量化表示
對這裡不熟悉,就要不厭其煩的重新梳理,反饋。那麼,
- 假設輸入的A[0]是nx個特徵值,8個樣本,A向量的維度是(nx,8);
- 輸入第一層,W.dot(A[0])需要成立,W的維度是(n[L],nx(n[L-1])), WA的維度是(n[L],8);Z的維度是(n[L],8),這個Z代表有8個樣本,每個樣本都是n[L]維度的列向量。
借用一下別人總結的,我覺得非常好。
Parameters vs Hyperparameters
引數和超引數