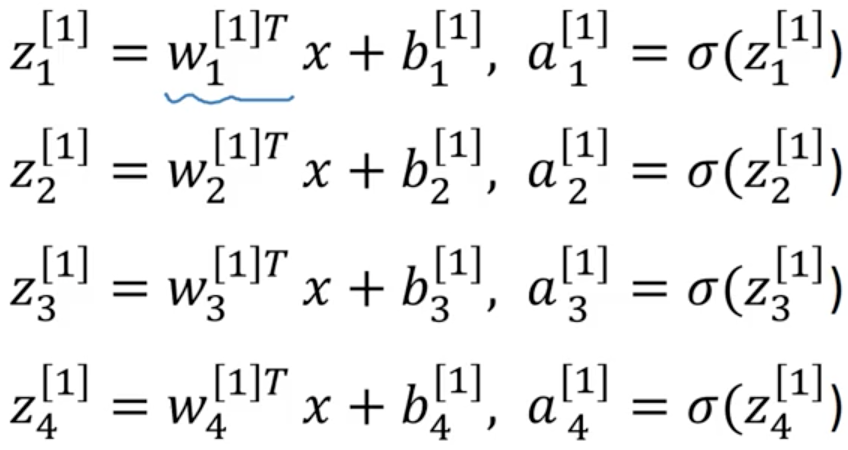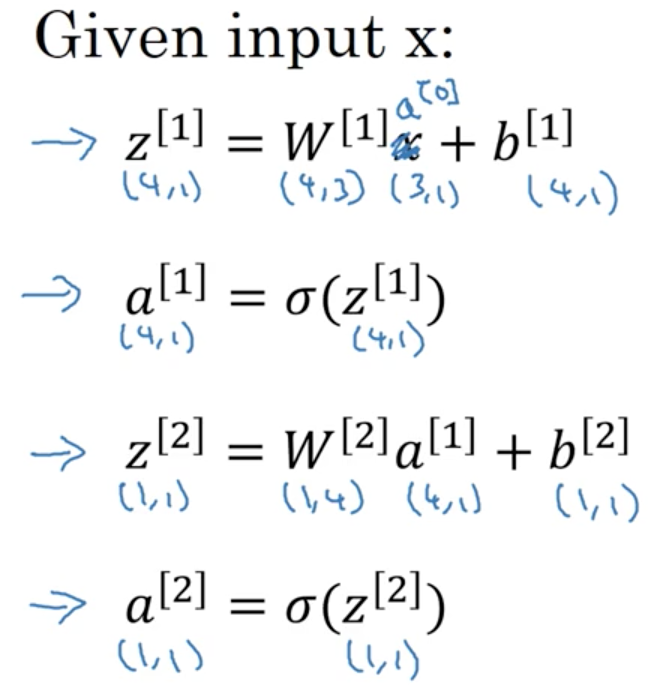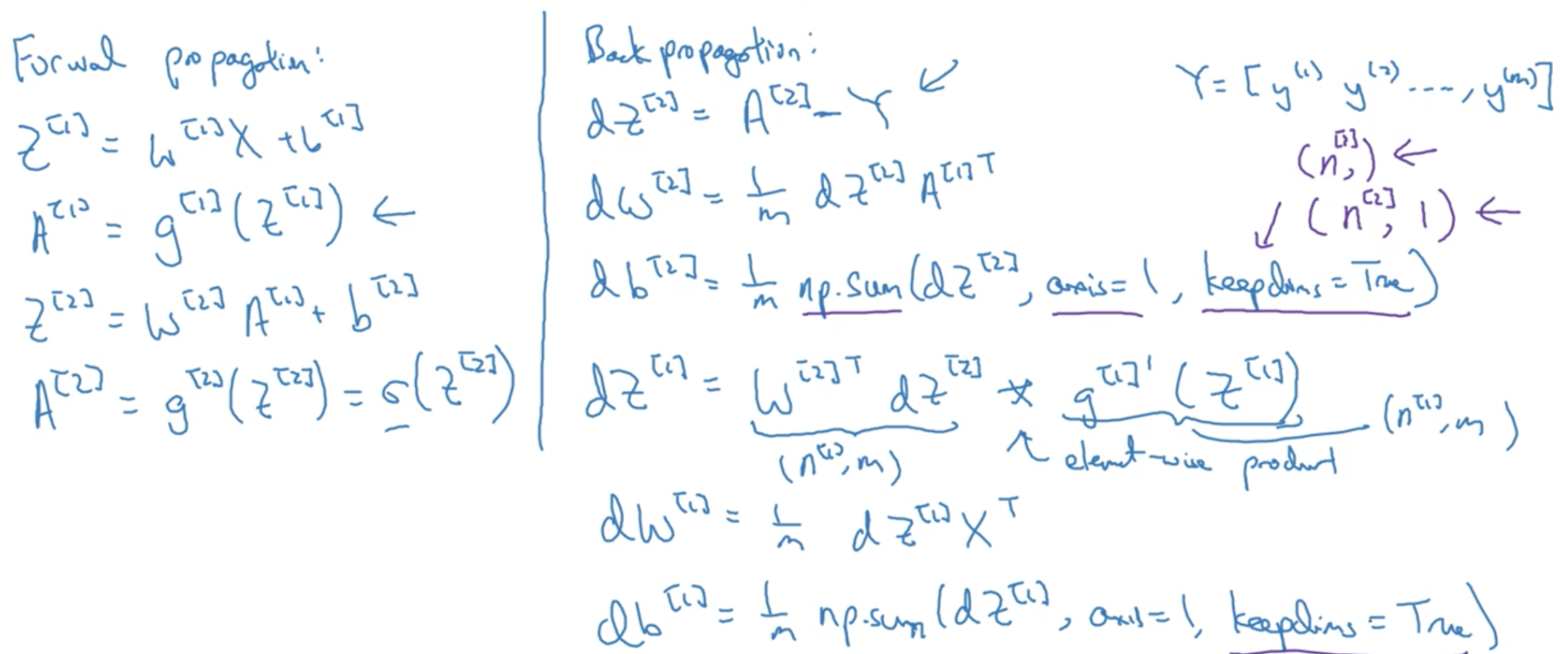Overview of Neural Network

回顧第一週的neural network，第一個neural network是z，第二個是theta，上一個傳入下一個。

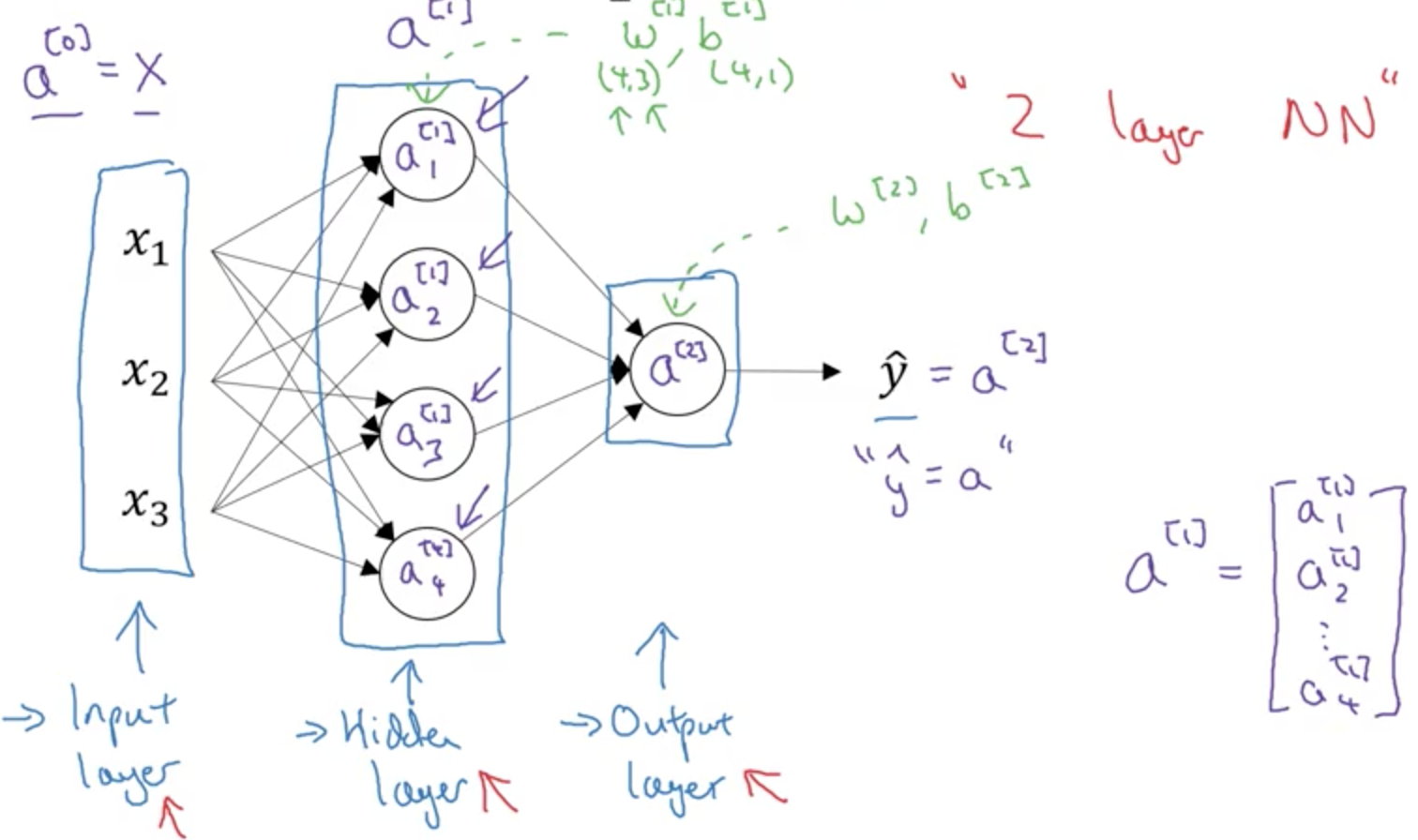
拿單層神經網路來說，樣本的值x1,x2...xn是input layer，是輸入層；hidden layer是function layer，負責把input layer的值進行處理，然後傳入output layer。傳出來的值就是y-hat，相當於函式處理的值。

下面來推倒神經網路的計算過程：

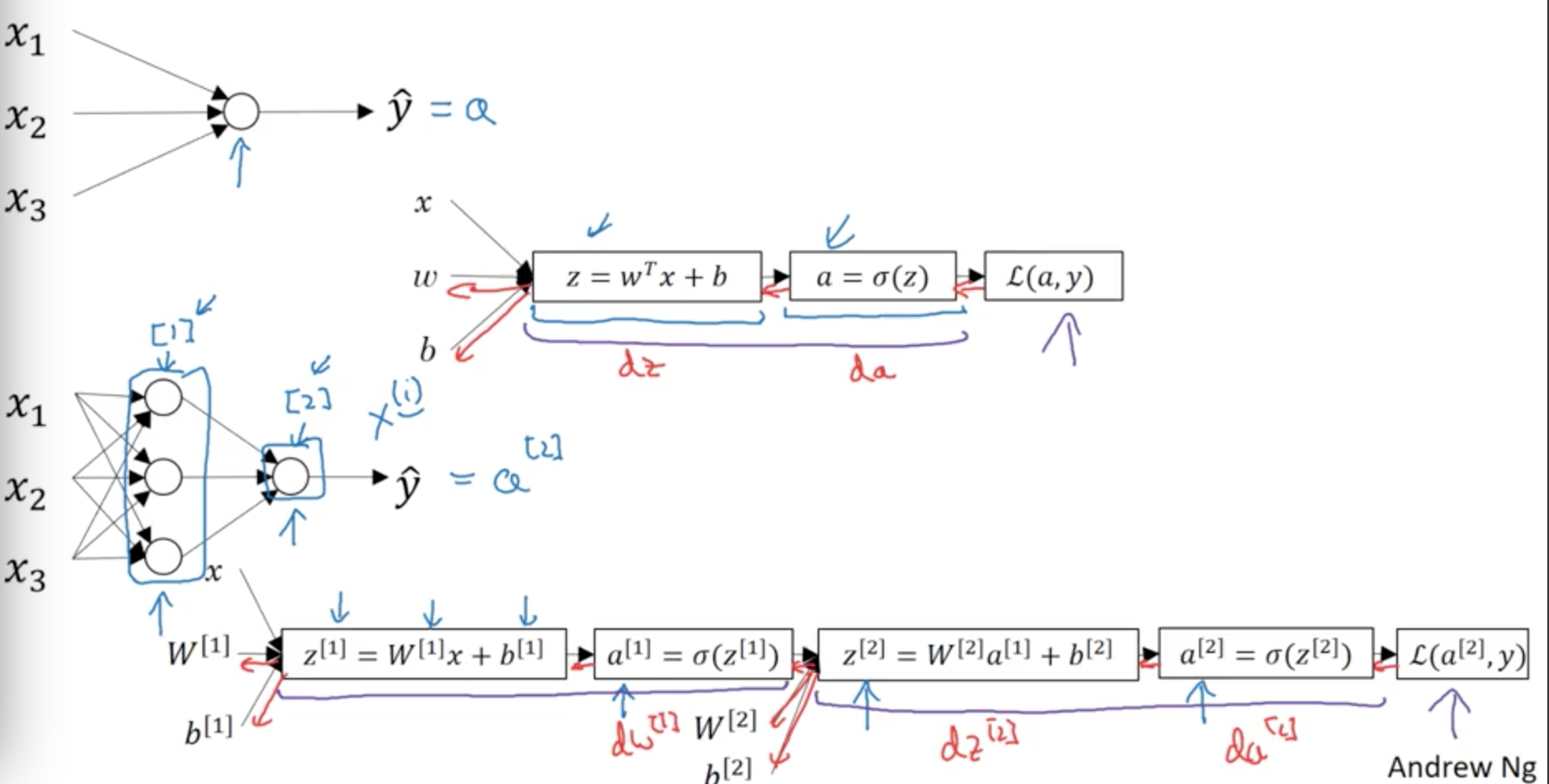
前面說過兩層神經網路可以看成邏輯迴歸再重複計算一次。

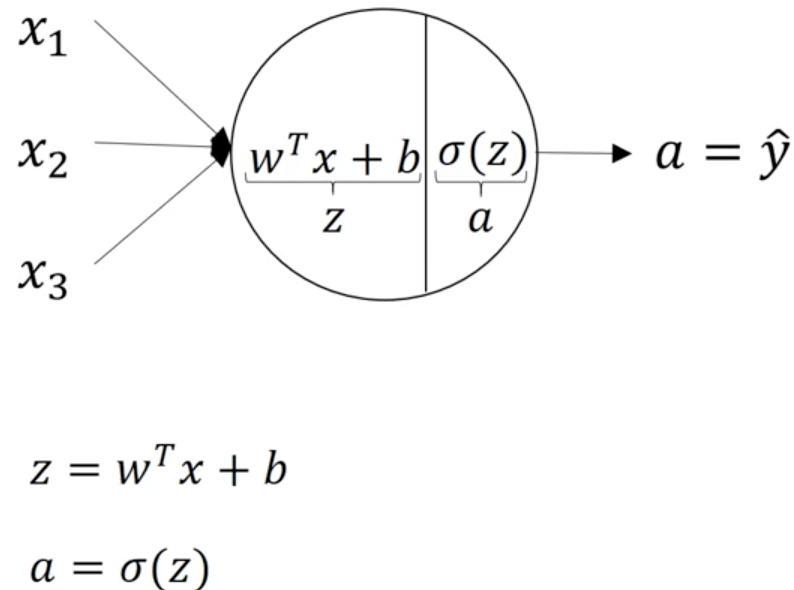
這是邏輯迴歸正向傳播應該執行的計算，先計算z，後計算a；對於一個雙層神經網路來說，一個node對應一次運算，那麼從輸入層到隱藏層有一次邏輯迴歸運算；從隱藏層到輸出層還有一次。

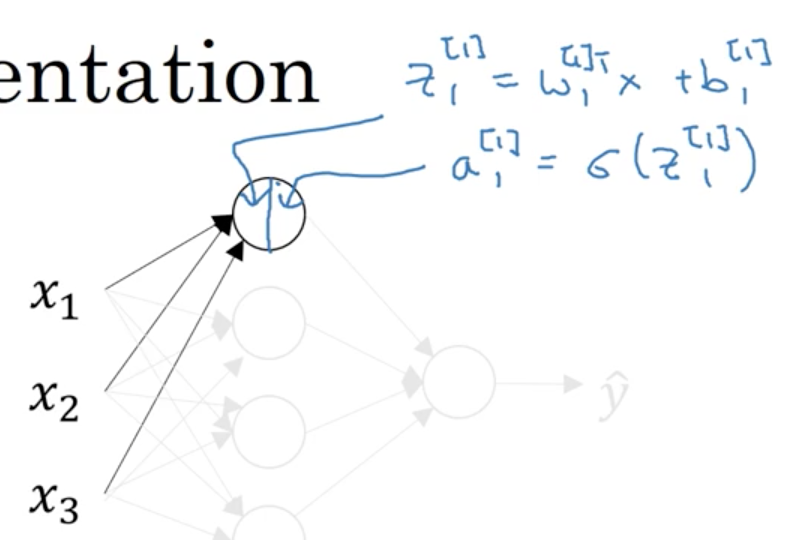
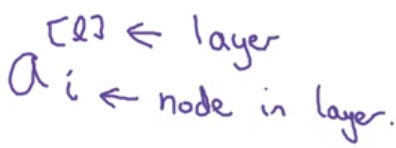
對於輸入層之後的隱藏層，我們用上標加方括號表示，[1]代表第一個隱藏層；下表代表這個節點的順序；

那麼，對於這個神經網路來說：

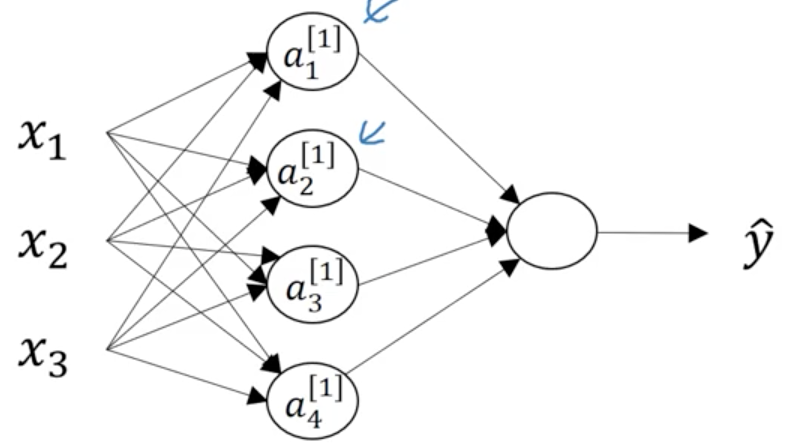
這裡面，四個node代表四個邏輯迴歸的計算（sigmoid），因為layer是從0開始的，所以input layer是a[0]；X = [ x1,x2,x3].T；

hidden layer是a[1]；y-hat layer 是 a[2]；那麼；

注意，在第二層時，W和b的維度就和layer 1不同了；並且引入了verctorization加快計算；

Vectorizing across multiple examples

對於有很多的樣本來說，z[1](i)代表，第一個隱藏層的第i個樣本；那麼，X是（n，m）的維度；W^[1]的維度是（1，n）的矩陣；b的維度是（1，m）；那麼，z的維度是（4，m）；A也是；4代表神經元個數，也相當於神經元特徵；那麼，行代表神經元個數；列代表樣本個數。這樣，就能向量化很多的樣本。

Activation functions

神經網路隱藏層和輸出層都需要啟用函式（activation function），在之前的課程中我們都預設使用Sigmoid函式σ(x)作為啟用函式。其實，還有其它啟用函式可供使用，不同的啟用函式有各自的優點。

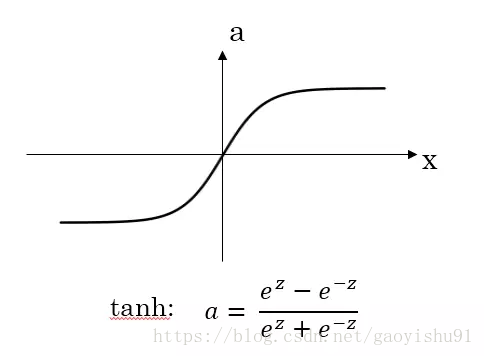
從圖上可以清楚地看到，每個啟用函式(activation function)的取值範圍和斜率。首先，sigmoid函式來說，取值範圍是（0，1），斜率是兩邊小，中間大；優點，該函式在最後一個神經元可以做啟用函式，因為最後一個神經元是輸出標籤{0，1}，道理不言而喻吧；對於隱藏層的啟用函式，一般來說，tanh函式要比sigmoid函式表現更好一些。因為tanh函式的取值範圍在[-1,+1]之間，隱藏層的輸出被限定在[-1,+1]之間，可以看成是在0值附近分佈，均值為0。這樣從隱藏層到輸出層，資料起到了歸一化（均值為0）的效果。

ReLU函式在z大於零時梯度始終為1；在z小於零時梯度始終為0；z等於零時的梯度可以當成1也可以當成0，實際應用中並不影響。對於隱藏層，選擇ReLU作為啟用函式能夠保證z大於零時梯度始終為1，從而提高神經網路梯度下降演算法運算速度。但當z小於零時，存在梯度為0的缺點，實際應用中，這個缺點影響不是很大。

為了彌補這個缺點，出現了Leaky ReLU啟用函式，能夠保證z小於零是梯度不為0。

Why do you need non-linear activation functions

我們為什麼需要非線性的啟用函式？因為如果都是線性函式，那麼第一個隱藏層計算完後，結果仍然是線性的，和有沒有隱藏層一樣。但是如果模型是做一個迴歸模型，也就是預測值，那麼在輸出層可以是線性模型，因為需要輸出一個連續值。

Derivatives of activation functions

在計算神經網路反向傳播的過程時，肯定是需要計算啟用函式的倒數的，（回想一下，前面的數的倒數就是後面倒數的乘積），那麼，肯定首先要了解每個函式的導數的求導嘛~

   sigmoid函式                tanh函式

 Relu函式                    Leaky Relu函式

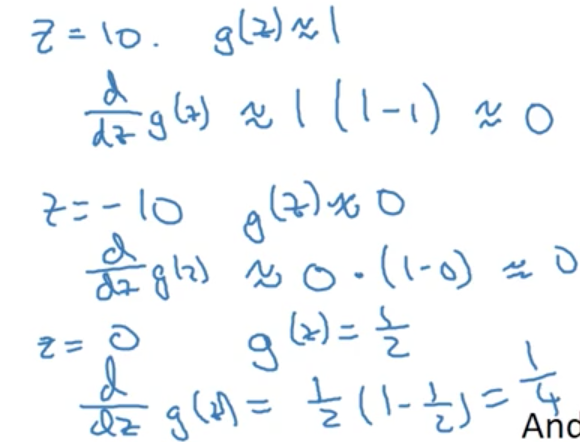
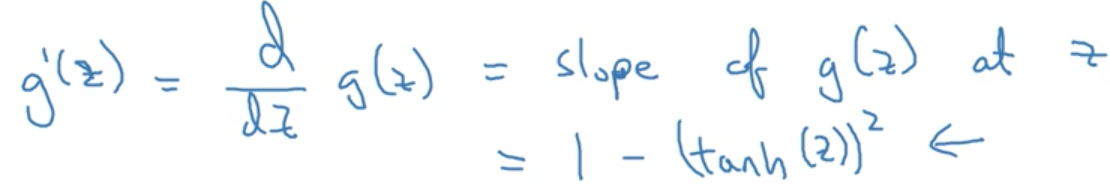
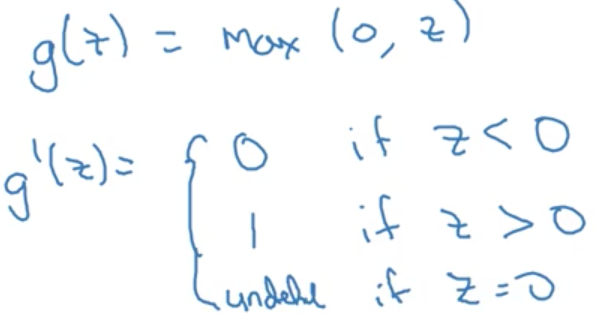
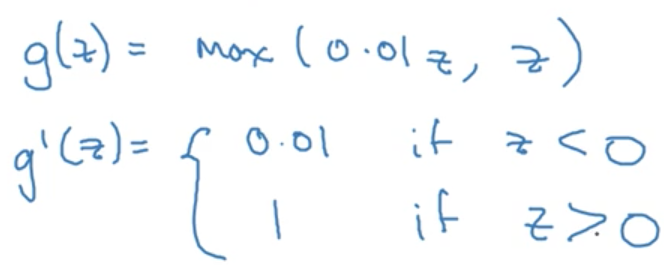
Gradient descent for neural networks

反向傳播是計算導數（梯度）的過程，這裡列出了正向傳播和反向傳播的比較，可以看到：

正向傳播是計算loss function的，反向傳播是計算梯度下降的，因為你要分別計算w和b的變化，所以需要知道他們的導數。

Random Initialization

神經網路模型中的引數權重W是不能全部初始化為零的，為什麼呢？

因為全部初始化為0，