什麼是PCA

• 主分析方法（PCA），是運用線性代數的知識，找到一個k維空間(k小於n, n為原來 樣本的維度)讓原來的樣本投影到該空間後能保留最大的差異程度，具體表現為方差。

• 舉個一個簡單的例子就是，全班同學的成績語文相差很大，從50到90分佈，但是英語成績大家都考到90多分，如果兩個成績都用同樣的比重區分排名，那麼英語的作用就不這麼明顯，而且需要考慮兩科成績。
  這時如果我新建一個新變數，對兩科取不同權重，這樣計算出來的新維度即能保留原來的特徵，又能達到降維的效果。
  這只是幫助理解，具體實現應該有出入。

• 具體是先把樣本寫成矩陣形式，求出協方差矩陣（自己跟自己的轉置相乘再除於樣本數）。協方差有個特殊的性質就是，對角線上的元素代表元素的方差，其他位置的元素代表協方差，就是不同元素的相關程度。

• 這時我們需要構造一個向量，令到協方差矩陣只留下對角線上的元素，其他位置的為0，其物理含義就是使原本元素投影到新空間後，每個維度之間的相關最小，而差異最大。這時再對對角線上的元素排序，選出最大的方差就達到降維的效果。至於怎麼實現矩陣對角化，就是數學的知識了。

什麼是SVM

• 支援向量機器（SVM），就是找到一個最佳超平面，把各類樣本分開，具體數學思想目前沒搞懂。只知道個大概或者說只能理解而二維的情況，汗。

我們來做題吧

• 手寫數字識別引用的是MNIST的樣本庫，train.csv是一個42000*785的資料集，有42000個樣本，第一列是label，後面784是灰度值。 train.csv是測試集，28000個樣本。

• 第一次參考別人的隨機樹演算法，採取n=200的引數，獲得了0.9668的效果。

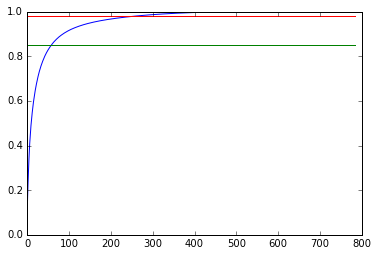
• 想想可以用PCA先降維，那麼問題來了，降到多少維了？一般是 （留下的方差總和） / （總方差和） = 85% 到 95%的區間，不說了，直接上測試程式碼。PCA函式內的n_components當填小數時是留下方差的百分比，不填就是全部保留，mle是自動。

from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import pandas as pd

pca = PCA(whiten=True)
digit = pd.read_csv('train.csv'
 
)
train = digit.values[1:, :].astype(int)
pca.fit(train)
exr = pca.explained_variance_ratio_

x = []
y = []
line85 = []
line98 = []
for i in range(len(exr)) :
    x.append(i)
    line85.append(0.85)
    line98.append(0.98)
    if i == 0: 
        y.append(exr[0])
    else:
        y.append(exr[i]+y[i-1])

plt.plot(x, y)
plt.plot(x, line85)
plt.plot(x, line98)
plt.show()

• 實驗圖片,通過pca降維器的屬性可以檢視留下幾個維度，具體用法百度吧。可見98%大概是154個左右。

• 然後後面是實驗程式碼

# -*- coding: utf-8 -*-
from sklearn.decomposition import PCA
from sklearn.svm import SVC
import pandas as pd
import numpy as np

pca = PCA(n_components=0.95, whiten=True)
digit = pd.read_csv('train.csv')
test = pd.read_csv('test.csv')
label = digit.values[:, 0].astype(int)
train = digit.values[:, 1:].astype(int)
test_data = test.values[:, :].astype(int)

pca.fit(train)
train_data = pca.transform(train)

svc = SVC()
svc.fit(train_data, label)

test_data = pca.transform(test_data)
ans = svc.predict(test_data)

a = []
for i in range(len(ans)):
    a.append(i+1)

np.savetxt('PCA_0.95_SVC.csv', np.c_[a, ans], 
    delimiter=',', header='ImageId,Label', comments='', fmt='%d')

• 調引數總共調了三次：
  
  1. 第一次用0.95，結果是0.9737。
  2. 第二次用0.85，結果是0.9815。
  3. 第三次直接試保留10個維度，結果是0.9341，比之前低了許多。

Summary

保留主要的特徵維度，能提高分類器的魯棒性，但是選取維度過少，會丟失了一些特徵資訊。參考別人的用了35的維度，取得的效果會好一點點。但是過度調引數感覺沒什麼意思。懂個大概思路就好，這次實驗自己看了sklearn參考文件的PCA內容，雖然有些看不懂，但是也是一種鍛鍊吧。

Keep Fighting！