【阿庫婭教你X程式碼】PlayFair密碼——0
大家好,我是
PlayFair密碼演算法的主要構成:金鑰、PlayFair代換表(PF表)、(約定的)填充字母、加密演算法、解密演算法
Playfair密碼(英文:Playfair cipher 或 Playfair square)是一種替換密碼,1854年由查爾斯·惠斯通(Charles Wheatstone)的英國人發明。
PF表是利用金鑰填充形成的加密表,而加密規則如下(解密規則逆行之):
- 若p1 p2在同一行,對應密文c1 c2分別是緊靠p1 p2 右端的字母。其中第一列被看做是最後一列的右方。如,按照前表,ct對應dc
- 若p1 p2在同一列,對應密文c1 c2分別是緊靠p1 p2 下方的字母。其中第一行被看做是最後一行的下方。
- 若p1 p2不在同一行,不在同一列,則c1 c2是由p1 p2確定的矩形的其他兩角的字母(至於橫向替換還是縱向替換要事先約好,或自行嘗試)。如,按照前表,wh對應tk或kt。
Notic:
- I/J是看成同一個,實際這個表中只要25個字母,這種設計阿庫婭都能明白,因為26-1剛好得到5x5的矩陣(實際戰爭中使用時,被去掉的字母是z,因為它出現頻率最低)
- 密文永遠是雙數,分組後也永遠沒有哪一組是倆字母相同的!
下面我們先來分解筆算步驟,然後通過程式模擬來實現演算法。
Step0.約定好金鑰和用來填充的字母,比如:
- 金鑰 = abbcdef
- 約定的字母 = z
Step1.寫出PlayFair代換表:
顯然,不能直接把eddcbaf寫進去,因為由一個金鑰得到的PF代換表實際是25個字母的一種唯一排序,所以需要去重。然後先填充去重後的金鑰,再填充金鑰中不包含
- 去重:edcbaf
- 填充PF表:
| e | d | c | b | a |
|---|---|---|---|---|
| f | g | h | i/j | k |
| l | m | n | o | p |
| q | r | s | t | u |
| v | w | x | y | z |
Step2.0 對明文加密:
2.0.1:明文預處理
- 分組&插入
因為加密運算就是在對兩個一組的不同字母的代換,所以先分組,相同的要插入那個
約定的字母(此例為z,顯然一個是不夠的,可以讓z是預設,還要一個預備的約定字母來頂替遇上“zz”的情況) - 補齊
經過若干次分組&插入後,如果剛好最後一組只有一個字母,就要尾部填充一個約定的字母 - 顯然,被進行上述明文預處理的明文才是真正參與到PF加密、解密的明文。想要徹底還原成原樣阿庫婭當然知道,就是不告訴你→_→
- 極端のexample:
原始明文:zzzz ——>分組:zz zz ->插入:(假設還有個預備的約定字母a)預設字母插入失敗,使用預備字母插入 ——>(分組然後插入若干次後) ——>za za za z ——>補齊(也就是真正的明文,簡直炫酷,認不出來系列): za za za zj
2.0.2:對明文加密
根據PF的規則,對兩個一組的字母的位置進行判斷
屬同一列,下邊的咯
屬不同行不同列的,就讓這倆字母的行列構成一個四邊形,定位得到的對角就是密文,同行的才對應
正常のexample:
明文 : 最近的動畫到處是暗牧,光腚局我fxxk oo (嗶!~)!
分組:最近 的動 畫到 處是 暗牧 光腚 局我 fx xk oo —–其中oo相同,插入z ———變成:fx xk oz o
- 分組後是單數,補齊:fx xk oz oz
- 預處理後明文:最近的動畫到處是暗牧光腚局我fxxkoofxxkozoz
- 加密:fx —–在pf表中這倆字母不同行不同列,那就根據其這個畫個四邊形,找到另外兩個對角的字母hv
(不是vh,同行才是對應關係)
如果密文是ed ,那就是同行,密文就是cb(這種是毗鄰的密文,要跳過密文,不是dc)。
同行相似~
Step2.1對密文解密:
無非就是對2.0.2的反向操作
- 同行那就左邊咯
- 同列那就上邊咯
- 不同行不同列?對角定位,同行對應咯(顯然,這個操作正反一樣的)
是不是很簡單?是不是很簡單?是不是很簡單?
程式碼還沒開始寫呢。
下面開始把以上筆算步驟翻譯成程式碼
因為是阿庫婭,所以註釋有點多,程式碼看不下去先看註釋:
正式開始のstep0:初始化必要資訊:
<c++>
int main(){
string key; //———————————————————————————— 宣告一個字串,放金鑰
string cleartext; //—————————————————————————— 宣告一個字串,明文
cout << "請輸入金鑰: " ;getline(cin, key);
cout << "請輸入明文: " ;getline(cin, cleartext);
string playfair[5][5] ; //—————————————————————— 宣告空的PF表
string another; //———————————————————————————— 約定填充的字母
cout << "輸入約定的填充字母: ";cin >> another;
}
</c++>
接著我們來看看step1:填充PF代換表
- 預備:
- 先介紹下下面兩個重要的變數:alp[3][26] 以及 abLength
- abLength就是字母填入PF表的序號`——>程式碼:int abLength=0;
- alp你可以可以用字母表來稱呼它
alp[3][26]在我眼裡是這樣的:(這是初始化狀態)
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
程式碼:int alp[3][26] = {{0*26},{0*26},{0*26}};//———————初始化為全0,即3x26個0
(注意了,alp這個實際是沒有a~z那行的,我用陣列下標加上97就剛好得到對應字母的ASCLL碼了。也就是alp[][i] 對應 char = i+97)
那麼它們有啥用呢?
- 首先,這裡step1需要從筆算那裡轉換一下思路。因為 填入pf表 等於先填入 金鑰中的字母 再填入 剩下的字母,所以我們要利用 字母表 第0行的值作為標識,1就是已經填了的、金鑰出現過了的,0表示未出現過
- 其次,第1行和第2行是用來儲存各個字母在PF表中的座標的,後面會用到,而在座標是在填入PF表時得到的,所以我們在填充PF表時也要順便填 字母表 後兩行
- 如何根據填入的序號求座標?
row = ablength/5 , line = ablength%5
順便要把row、line填進alp[1][]、alp[2][]中
先使用金鑰填充
為了讓金鑰中的字母只在pf表中填充一次,所以我用alp第0行的0/1值來標記它們。我們約定0代表未用,1代表已用。- 遍歷金鑰,檢查 該字母的alp[0][] ,若為0,則用當前序號(abLength)求座標寫入PF表,並在alp中記錄下來,abLength++。
若為1,跳過
- 遍歷金鑰,檢查 該字母的alp[0][] ,若為0,則用當前序號(abLength)求座標寫入PF表,並在alp中記錄下來,abLength++。
Example:金鑰第一個是e,那麼 key[0] 強轉 int型 就是 e的ASCLL值 ,再減去97就剛好是 alp中e的陣列下標。此時alp[0][ (int)key[0] - 97] 等於0的話,說e不在pf表中,那就標記為1,並且根據 abLength 等於0求得e的座標為 row = 0/5, line = 0%5,把row、line記錄到alp中並且把e寫入到 PlayFair[0][0] 位置
- NOTICE:I/J記得看成同一個
for(int i=0 ; i<key.length() ; i++){//————————————————————遍歷金鑰
if(alp[0][((int)key[i]) - 97] == 0){ //——————————————(int)表示強轉,列標引數表示金鑰正在考察的那個字母的ASCLL值-97,其對應行標如果等於0,說明沒重複,那就放進PF表,並且根據序號填座標入字母表,第0行寫入1表示已用
if(key[i] == 'i'||key[i] == 'j'){ //—————————————這個判斷顯然就是為了讓I/J一致,遇上I/J,要兩個一起處理
alp[0][8]=alp[0][9]=1;
//注意裡面的運算:用序號求座標
playfair[abLength/5][abLength%5] = key[i];
//新增alp在playfair裡面的對應座標
alp[1][8]=alp[1][9] = abLength/5;
alp[2][8]=alp[2][9] = abLength%5;
//弄完了序號加一
abLength++;
}
else{
alp[0][((int)key[i]) - 97] = 1;
playfair[abLength/5][abLength%5] = key[i];
alp[1][((int)key[i]) - 97] = abLength/5;
alp[2][((int)key[i]) - 97] = abLength%5;
abLength++;
}
}
}
用剩下的字母填充PF表與字母表
for(int i = 0 ; i<26 ; i++){//————————————————————顯然是for:a~z的遍歷,i作為alp的列標 if (i == 8){ //———————————————————————————————i作為順數第⑨個字母,在陣列當然列標是⑧ if(alp[0][i] == 0){ char x =i+97;//———————————————————————強制轉換 playfair[abLength/5][abLength%5] = x; //i和i+1一起處理,也就是I/J一起處理 alp[1][i] = abLength/5; alp[2][i] = abLength%5; alp[1][i+1] = abLength/5; alp[2][i+1] = abLength%5; abLength++; alp[0][i+1] = 1; } } else if(alp[0][i] == 0 ){ char x =i+97; playfair[abLength/5][abLength%5] = x; alp[1][i] = abLength/5; alp[2][i] = abLength%5; abLength++; }}
此時PF表填充完畢,不信?你自己列印處理試試(就是I/J那個有點坑爹,加個判斷即可)
為大家補充一份碉堡的程式框圖(就這部分)
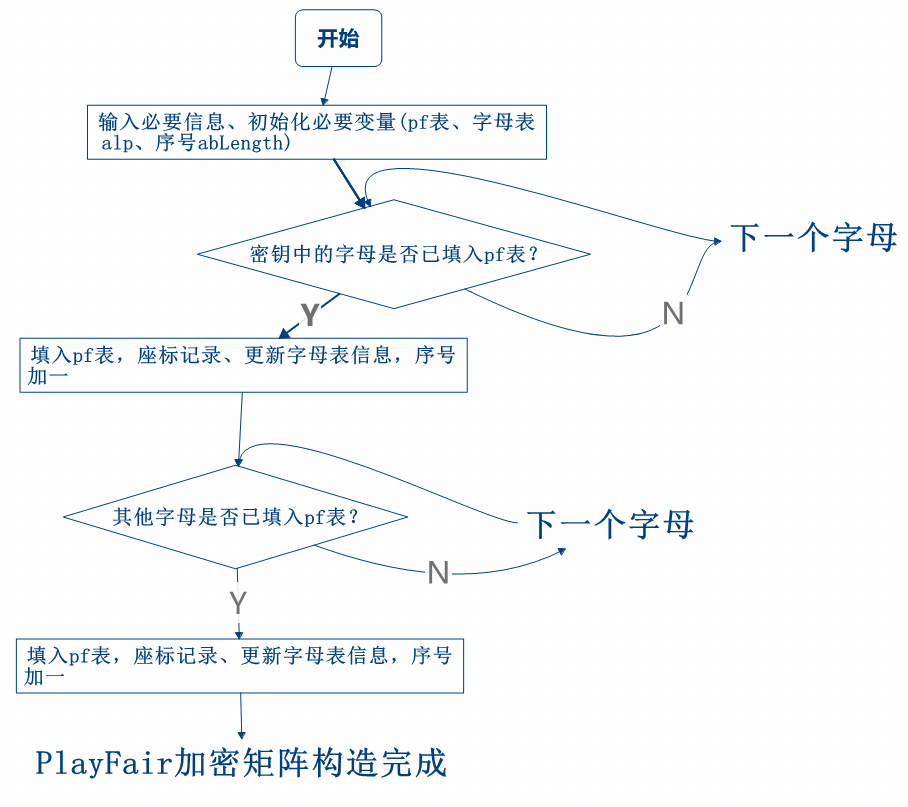
今天先到此為止,蟹蟹



