(矩陣快速冪)解所有類似Fibonacci 的題目
Description
In the Fibonacci integer sequence, F0 = 0, F1 = 1, and Fn = Fn − 1 + Fn − 2 for n ≥ 2. For example, the first ten terms of the Fibonacci sequence are:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
An alternative formula for the Fibonacci sequence is
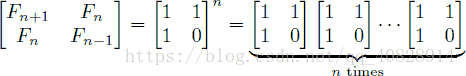
Given an integer n, your goal is to compute the last 4 digits of Fn.
Input
The input test file will contain multiple test cases. Each test case consists of a single line containing n (where 0 ≤ n ≤ 1,000,000,000). The end-of-file is denoted by a single line containing the number −1.
Output
For each test case, print the last four digits of Fn. If the last four digits of Fn are all zeros, print ‘0’; otherwise, omit any leading zeros (i.e., print Fn mod 10000).
Sample Input
0
9
999999999
1000000000
-1
Sample Output
0
34
626
6875
這個題是出題人好心,直接把規律給我們找出來了,那我們就只需要求那個矩陣的n次方,然後輸出a[0][1]即可
1.先說說矩陣快速冪
為了類比快速冪,我們先寫出快速冪的程式碼
快速冪求x的y次方,是把y看作二進位制來的,矩陣快速冪也一樣。
區別:
1.矩陣快速冪底數是矩陣,ren是矩陣
2.最終矩陣乘矩陣還是矩陣,也就是說函式返回矩陣,ans是矩陣
3.我們存答案的ans初始化應該是初等矩陣
所以涉及到矩陣的程式碼我們都要改
int pow_1(int 改完之後就是這樣了
struct matrix
{
LL x[2][2];
};
matrix mutimatrix(matrix a,matrix b)
{
matrix temp;
memset(temp.x,0,sizeof(temp.x));
for(int i=0;i<2;i++)
for(int j=0;j<2;j++)
for(int k=0;k<2;k++)
{
temp.x[i][j]+=a.x[i][k]*b.x[k][j];
temp.x[i][j]%=mod;
}
return temp;
}
matrix k_powmatrix(matrix a,LL n)
{
matrix temp;
memset(temp.x,0,sizeof(temp.x));
for(int i=0;i<2;i++)
temp.x[i][i]=1;
while(n)
{
if(n&1)
temp=mutimatrix(temp,a);
a=mutimatrix(a,a);
n>>=1;
}
return temp;
} 這個出題人直接把意思說的明明白白的,直接求那個矩陣的n次方就ok
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
#define LL long long
const int mod=10000;
struct matrix
{
LL x[2][2];
};
matrix mutimatrix(matrix a,matrix b)
{
matrix temp;
memset(temp.x,0,sizeof(temp.x));
for(int i=0;i<2;i++)
for(int j=0;j<2;j++)
for(int k=0;k<2;k++)
{
temp.x[i][j]+=a.x[i][k]*b.x[k][j];
temp.x[i][j]%=mod;
}
return temp;
}
matrix k_powmatrix(matrix a,LL n)
{
matrix temp;
memset(temp.x,0,sizeof(temp.x));
for(int i=0;i<2;i++)
temp.x[i][i]=1;
while(n)
{
if(n&1)
temp=mutimatrix(temp,a);
a=mutimatrix(a,a);
n>>=1;
}
return temp;
}
int main()
{
int n;
while(cin>>n ){
if(n==0) {
cout<<"0\n";
continue;
}
if(n==1||n==2) {
cout<<"1\n";
continue;
}
if(n==-1) return 0;
matrix st;
memset(st.x,0,sizeof(st.x));
st.x[0][0]=1;
st.x[0][1]=1;
st.x[1][0]=1;
st.x[1][1]=0;
st=k_powmatrix(st,n);
printf("%lld\n",(st.x[0][1]+mod)%mod);
}
} 2.如何通過矩陣快速冪解決這種遞推問題
先看普通斐波那契
參考:https://blog.csdn.net/wust_zzwh/article/details/52058209
f(n)=f(n-1)+f(n-2)
f(1)=f(2)=1
其實這個是個遞推式,那麼我們只要找到他的通項,就可以求出n為任何值時候的f(n)
那這個遞推式我們看不出他是等比還是等差數列,通項也不會求,此時就需要用矩陣
因為矩陣有一個性質,一個常數矩陣乘以一個矩陣A(n),結果是矩陣B(n)
那如果A中各個元素對應於B中各個元素滿足,A(n)=B(n-1),那這個整體就是個等比數列啊
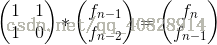
我們設an=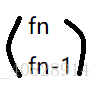
上面看作是q*a(n-1)=an,由等比數列通項公式得到
q^(n-1)*a1=an
現在q我們已經有了,就剩找a1了,a1我們都會求,帶特殊值麼,假設n=2,a2=q*a1,然後我們就求出a1了,所以之後求an就先求q^(n-1),再求q^(n-1) *a1
因為我是學過線性代數的,其實這有個大問題,矩陣的左乘右乘結果不一樣,為了方便起見,我們通項乘的次序應該和第一個遞推式的次序一樣
還有個例子
f(1) = 1, f(2) = 1, f(n) = (A * f(n - 1) + B * f(n - 2)) mod 7.
Given A, B, and n, you are to calculate the value of f(n).
圖片來自:https://www.cnblogs.com/Blackops/p/5468284.html
通過這一題我們明白一個事情,那就是對我們那個矩陣數列的優化,2* 1矩陣可以寫成2* 2矩陣,這樣的話我們不用再弄一個函式去求2* 1矩陣*2*2矩陣了
還有一點,關於n那個次冪的事,這都是看a1對應的那個n是幾,根小學學的等比數列一樣一樣的。。
還有個小竅門,我們不用一上來就推f(n),可以通過f(1),f(2)推f(3),推完之後把3變成n,1變成n-2,2變成n-1,然後帶4驗證。如果是,那就是,然後繼續ok
參考程式碼:
https://blog.csdn.net/elbadaernu/article/details/77899130
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
#define LL long long
const int mod=7;
struct matrix
{
LL x[2][2];
};
matrix mutimatrix(matrix a,matrix b)
{
matrix temp;
memset(temp.x,0,sizeof(temp.x));
for(int i=0;i<2;i++)
for(int j=0;j<2;j++)
for(int k=0;k<2;k++)
{
temp.x[i][j]+=a.x[i][k]*b.x[k][j];
temp.x[i][j]%=mod;
}
return temp;
}
matrix k_powmatrix(matrix a,LL n)
{
matrix temp;
memset(temp.x,0,sizeof(temp.x));
for(int i=0;i<2;i++)
temp.x[i][i]=1;
while(n)
{
if(n&1)
temp=mutimatrix(temp,a);
a=mutimatrix(a,a);
n>>=1;
}
return temp;
}
int main()
{
int a,b,n;
while(scanf("%d%d%d",&a,&b,&n))
{
if(!(a+b+n)) break;
if(n<=2)
{
printf("1\n");
continue;
}
matrix st;
memset(st.x,0,sizeof(st.x));
st.x[0][0]=a;
st.x[0][1]=1;
st.x[1][0]=b;
st.x[1][1]=0;
matrix init;
memset(init.x,0,sizeof(init.x));
init.x[0][0]=1;
init.x[0][1]=1;
st=k_powmatrix(st,n-2);
st=mutimatrix(init,st);
printf("%lld\n",(st.x[0][0]+mod)%mod);
}
return 0;
}