演算法講解:ac自動機及簡單衍生
AC自動機簡介:
首先簡要介紹一下AC自動機:Aho-Corasick automation,該演算法在1975年產生於貝爾實驗室,是著名的多模匹配演算法之一。一個常見的例子就是給出n個單詞,再給出一段包含m個字元的文章,讓你找出有多少個單詞在文章裡出現過。嗯沒錯,比如word文件等一系列帶有查詢功能的東西一般用的都是這種東西啦。要搞懂AC自動機,先得有字典樹Trie和KMP模式匹配演算法的基礎知識。KMP演算法是單模式串的字元匹配演算法,AC自動機是多模式串的字元匹配演算法。至於什麼有限狀態自動機之類的,就是自動機理論的之後的事情了。嘛,在後面補了一下有限狀態自動機的知識,有興趣可以去下面看。
AC自動機前置技能: trie樹和kmp。
trie樹呢,是一種儲存了一系列字元的樹,每個節點儲存一個字元,在一棵樹的分支進行遍歷,每次都會得到一個儲存好的字串。
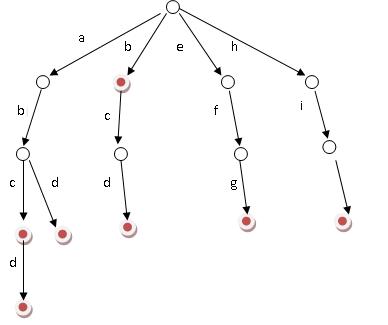
假設有b,abc,abd,bcd,abcd,efg,hii 這6個單詞,我們構建的樹就是如下圖這樣的:這樣就可以看出,查詢一個字串,那就直接順著這個串找下去就好了,唔,時間複雜度貌似是O(1)的
trie樹的用途也非常多,在這裡就先不展開分析了,一般用於字串的儲存,查詢之類的,具體問題可以參考我的其他題解。
這是poj2001的程式碼,trie樹裸題,可以作為參考。
#include<cstdio> #include<cstring> #include<algorithm> #include<cmath> #include<iostream> #include<vector> #include<string> using namespace std; const int MAXN=3000000; typedef long long ll; char s[10005][31]; struct node { int num; node* next[26]; node() { memset(next,NULL,sizeof(next)); num=0; } }; node* root=new node(); void build(char str[]) { node* p=root; int len=strlen(str); for(int i=0;i<len;i++) { int index=str[i]-'a'; if(p->next[index]==NULL) { p->next[index]=new node(); } p=p->next[index]; p->num++; } } void query(char str[]) { node* p=root; int len=strlen(str); for(int i=0;i<len;i++) { printf("%c",str[i]); int index=str[i]-'a'; p=p->next[index]; if(p->num==1) return; } } int main() { int T; int n=0; while(scanf("%s",s[n])!=EOF) { build(s[n]); n++; } for(int i=0;i<n;i++) { printf("%s ",s[i]); query(s[i]); printf("\n"); } return 0; }
下一個內容,kmp。
kmp是一種字串的演算法,貌似現在的strstr就是用kmp重寫的,用的最多的當然就是查詢一個字串中有沒有給定的字串,位置和個數了
因為樸素的查詢方法是O(n^2)的,其中由於進行了回溯,導致效率的下降,但問題在於,回溯過去的子串我們已經查詢過了,能否保留查詢的內容呢?答案當然是可以的。
我們可以用一個next陣列來儲存字首的值,每次失配就直接導向失配的上一個子串位置,從而減少了不必要的匹配過程,其中,next陣列的求解方式類似於動態規劃,事實上就是動態規劃的一種思想。在建立next陣列的時候就相當於對本串進行一次kmp匹配。雙指標掃兩個串的兩個點,同時前指標還有賦值的作用。
具體可以參照kmp的內容和程式碼,在此不做仔細講解.
以下是poj3461查詢一個字串對另一個字串的子串個數的程式碼,可以作為參考。
#include <iostream>
#include <cstring>
#include<cstdio>
using namespace std;
const int N = 1000002;
int nxt[N];
char S[N], T[N];
int slen, tlen;
void getNext()
{
int j=0,k=-1;nxt[0]=-1;
while(j<tlen)
{
if(k==-1||T[j]==T[k])
nxt[++j]=++k;
else
k=nxt[k];
}
}
int kmp()
{
int i=0,j=0,ans=0;
getNext();
while(i<slen)
{
if(j==-1||S[i]==T[j])
{
i++;
j++;
}
else
{
j=nxt[j];
}
if(j==tlen)
{
ans++;
j=nxt[j];
}
}
return ans;
}
int main()
{
int n;
scanf("%d\n",&n);
while(n--)
{
scanf("%s",T);
scanf("%s",S);
slen=strlen(S);
tlen = strlen(T);
printf("%d\n",kmp());
}
return 0;
}接下來就進入ac自動機的正題:
ac自動機就是一種多模的匹配演算法了,剛剛前置技能都已經講完了,就直擊原理,ac自動機本質上就是一棵trie樹,儲存了一系列單詞,但是和trie樹不同的是,在每個節點中都存有一個fail指標,用於儲存失配後所需要移動到的節點位置(是不是很眼熟,對了,就是kmp的next陣列嘛)
既然我們知道了 AC自動機是用來做什麼的,那麼我們就來說一說怎麼在 Trie上構造 AC自動機。
首先,我們看一下條轉時的條件,如同 KMP演算法一樣, AC自動機在匹配時如果當前字元匹配失敗,那麼利用fail指標進行跳轉。由此可知如果跳轉,跳轉到的串的字首,必為跳轉前的模式串的字尾。由此可知,跳轉的新位置的深度一定小於跳之前的節點。所以我們可以利用 bfs在 Trie上面進行 fail指標的求解。
下面,是具體的構造過程(和KMP是一樣的)。首先 root節點的fail定義為空,然後每個節點的fail都取決自己的父節點的fail指標,從父節點的fail出發,直到找到存在這個字元為邊的節點(向回遞迴),將他的孩子賦值給尋找節點。如果找不到就指向根節點,具體參照程式碼:
#include <iostream>
#include <cstring>
#include<cstdio>
#include<queue>
#include<algorithm>
using namespace std;
const int N = 1000002;
char s[1000100];
int n;
struct node
{
int cnt;
node* next[26];
node* fail;
node()
{
cnt=0;
fail=NULL;
memset(next,NULL,sizeof(next));
}
};
node *root;
void bfs()//通過bfs尋找fail指標的值
{
node *p=root,*tmp,*son;
queue<node*> q;
q.push(p);
while(!q.empty())
{
tmp=q.front();
q.pop();
for(int i=0; i<26; i++)
{
son=tmp->next[i]; //隊首元素的子節點
if(son!=NULL)
{
p=tmp->fail; //p作為儲存節點 表示類似kmp當前k的值
while(p!=NULL)
{
if(p->next[i]!=NULL)
{
son->fail=p->next[i];
break;
}
p=p->fail;
}
if(!p) son->fail=root;
q.push(son);
}
}
}
}
void insert() //和trie樹一樣的插入方式
{
node *p=root;
int len=strlen(s);
for(int i=0; i<len; i++)
{
int index=s[i]-'a';
//printf("%d\n",index);
if(p->next[index]==NULL)
{
p->next[index]=new node();
}
p=p->next[index];
}
p->cnt++;
}
void query()
{
int ans=0;
node* p=root,*tmp;
int len=strlen(s);
for(int i=0; i<len; i++)
{
int index=s[i]-'a';
while(p!=root&&p->next[index]==NULL) //kmp中的k=next[k]的相同思路
{
p=p->fail;
}
p=p->next[index];//下一節點
if(p==NULL)//匹配失敗 j=0
{
p=root;
}
tmp=p;
while(tmp!=root) //與kmp不同,找尋所有滿足子條件的節點。
{
if(tmp->cnt>=0)
{
ans+=tmp->cnt;
tmp->cnt=-1;
}
else
break;
tmp=tmp->fail;
}
}
printf("%d\n",ans);
}
int main()
{
int tt=0,T;
scanf("%d",&T);
while(T--)
{
root = new node();
scanf("%d\n",&n);
for(int i=0; i<n; i++)
{
scanf("%s",s);
//printf("%s\n",s);
insert();
}
bfs();
scanf("%s",s);
query();
}
return 0;
}
時間複雜度分析:
對於Trie的匹配來說時間複雜性為:O(max(L(Pi))L(T))其中L串的長度函式,P是模式串,T是目標串。
對於 AC自動機來說時間複雜性為:O(L(T)+max(L(Pi))+m)氣質m是模式串的數量。
對於 Trie 圖 來說時間複雜性為:O(L(T))在此的時間複雜性都是指匹配的複雜度。
對於構造的代價是 O(sum(L(Pi)))其中sum是求和函式。
嘛,因為學長說ac自動機太簡單了(orz)所以要求我擴充套件一下ac自動機的內容:
trie圖:
在講tire圖的時候,先科普一下有限狀態自動機的知識:
有限狀態自動機是具有離散輸入和輸出的系統的一種數學模型。 其主要特點有以下幾個方面: – (1)系統具有有限個狀態,不同的狀態代表不同的意義。按照實際的需要,系統可以在不同的狀態下完成規定的任務。 – (2)我們可以將輸入字串中出現的字元彙集在一起構成一個字母表。系統處理的所有字串都是這個字母表上的字串。 – (3)系統在任何一個狀態下,從輸入字串中讀入一個字元,根據當前狀態和讀入的這個字元轉到新的狀態。 – (4)系統中有一個狀態,它是系統的開始狀態。 – (5)系統中還有一些狀態表示它到目前為止所讀入的字元構成的字串是語言的一個句子。 形式定義 · 定義:有限狀態自動機(FA—finite automaton)是一個五元組: – M=(Q, Σ, δ, q0, F) · 其中, – Q——狀態的非空有窮集合。∀q∈Q,q稱為M的一個狀態。 – Σ——輸入字母表。 – δ——狀態轉移函式,有時又叫作狀態轉換函式或者移動函式,δ:Q×Σ→Q,δ(q,a)=p。 – q0——M的開始狀態,也可叫作初始狀態或啟動狀態。q0∈Q。 – F——M的終止狀態集合。F被Q包含。任給q∈F,q稱為M的終止狀態。用幾句話來概括就是:
|
把問題的求解過程劃分成離散的“狀態”,並用一個有向圖建立狀態(結點)的遷移關係。 實現一個程式單位,在給定初始狀態後,能夠根據輸入資訊實現狀態間的遷移,並可以在有限步驟後遷移到預定的“終態”。 在遷移的過程中,問題得到解決。//摘自網上 |
tire圖,說起來就是比ac自動機多了一個確定性
確定性是什麼?
非確定有限狀態自動機與確定有限狀態自動機的唯一區別是它們的轉移函式不同。確定有限狀態自動機對每一個可能的輸入只有一個狀態的轉移。非確定有限狀態自動機對每一個可能的輸入可以有多個狀態轉移,接受到輸入時從這多個狀態轉移中非確定地選擇一個。
trie圖中會有補邊這樣一個機制,而且在根節點儲存了所有字典中的字元從而滿足了trie圖的確定性:
也就是說,每一個確定的輸入字元都會給你一個確定的狀態節點
在ac自動機和trie圖中,區別就是ac自動機失配後可能需要進行多次轉移,但trie圖只需要一次轉移
Trie圖是AC自動機的確定化形式,即把每個結點不存在字元的next指標都補全了。這樣做的好處是使得構造fail指標時不需要next指標為空而需要不斷回溯。
比如構造next[cur][i]的fail指標,cur為父節點,next[cur][i]為cur的兒子結點,如果是AC自動機,如果父親結點tmp(tmp是cur的一份拷貝)的next[fail[tmp]][i]不存在時,需要讓tmp不斷回溯(即tmp = fail[tmp]),直到next[fail[tmp]][i]不為空時,才讓fail[next[cur][i]] = next[fail[tmp]][i]。
如果是Trie圖,那麼直接讓fail[next[cur][i]] = next[fail[cur]][i]就可以了,因為Trie圖已經補全了next指標。
嘛 ac自動機和trie圖中的區別網路中眾說紛紜,不管了,具體名詞可能有所區別,但思想是不會變的
由於其實和ac自動機使用上幾乎沒有區別,實戰上使用次數不多,以下就發一個程式碼作為trie圖的總結。(在敲模板時發現trie圖要比ac自動機好寫一點,嘛,不過根據先入為主的原則,還是ac自動機要順手吧)
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
struct Trie
{
int flag;
struct Trie* behind;
struct Trie* next[26];
};
int main()
{
int n;
char s[100001];
cin >> n;
Trie* root = new Trie;
for (int i = 0; i < 26; i++)
{
root->next[i] = NULL;
}
root ->behind = NULL;
root ->flag = 0;
while (n--)
{
cin >> s;
Trie* p = root;
for (int i = 0; s[i]!='\0'; i++)
{
int j = s[i] - 'a';
if (!p->next[j])
{
Trie* q = new Trie;
q->flag = 0;
for (int k = 0; k < 26; k++)
{
q->next[k] = NULL;
}
q ->behind = NULL;
p->next[j] = q;
}
p = p->next[j];
}
p->flag = 1;
}
queue<Trie*> Q;
root->behind = root;
for (int i = 0; i < 26; i++)// 和ac自動機的差別哦,初始狀態補邊
{
if(!root->next[i])
{
root->next[i] = root;
}
else
{
root->next[i]->behind = root;
Q.push(root->next[i]);
}
}
while(!Q.empty())
{
Trie *p = Q.front();
Trie *q = p->behind;
Q.pop();
for (int i = 0; i < 26; i++)
{
if(!p->next[i])
{
p->next[i] = q->next[i];
}
else
{
p->next[i]->behind = q->next[i];
Q.push(p->next[i]);
}
}
}
char article[1000001];
Trie* p = root;
cin >> article;
bool tag = false;
for (int i = 0; article[i]!='\0'; i++)
{
int j = article[i] - 'a';
p = p->next[j];
if(p->flag == 1)
{
tag = true;
cout << "YES" <<endl;
break;
}
}
if(tag == false)
cout << "NO" <<endl;
return 0;
}
fail樹:
因為本人太弱嘛,只能初步簡單的提一下fail樹及其應用。 fail樹呢,是將ac自動機(trie圖)中的所有fail指標反向,但是不管是Trie圖還是AC自動機,它們的fail指標的指向都是一模一樣的。 我們可以發現,因為一個點只會引出一個fail指標,所以反向之後就證明任意一個點只會有一個點指向他,那就說明這個點的父親節點只有一個,可知該圖是一棵樹。我們稱之為fail樹fail樹的應用:
如果有n個字串,所有字串的長度加起來不超過106,有m個查詢,要查詢第x個字串在第y個字串中出現了多少次。
如果是使用AC自動機查詢,可以直接對字串構建AC自動機,然後讓y去走AC自動機,對於走過的結點,把其權值加1。那麼要查詢x在y中出現了多少次,便要從底層開始,順著fail指標把權值上傳。然後只要查詢x結點的權值是多少就知道x在y中出現了多少次。每次查詢的複雜度是O(tot+len[y]),其中tot是AC自動機的結點總數。很多oj上就會直接把ac自動機的方法卡掉
如果是使用Fail樹進行查詢,那麼只要查詢所有子結點的權值和就好了,子結點的權值和可以使用dfs序和樹狀陣列來維護。然後同樣讓有去走AC自動機,將走過的結點的權值加1,只不過現在是用樹狀陣列來維護權值。那麼要查詢x在y中出現了多少次,只要進行一次區間查詢就可以了,即只要查詢x結點的所有子結點就好了(根據fail樹的性質),因為其dfs序號是連續的,所以是一次區間查詢。可以將查詢按照y排序,然後對具有相同y的查詢一起查詢。每次查詢時間複雜度是O(len[y]+log(tot))。