大數運算

開發環境：Visual Studio 2015

主要技術：string,C++類

專案描述：

1.對於計算機不能進行計算的大資料進行處理，讓計算機實現大資料的讀入、輸出和基本運算；

2.使用C++類將超過內建型別(long long int)範圍的數轉換成字串進行儲存，並將儲存大數的字串拆開進行分析，逐位進行運算儲存,即將大數問題分解成單個字元的相互運算；

3.實現大數的讀入，輸出以及大數的加，減，乘，除運算功能。

大數運算的實現方法主要有以下幾種：

（1） 用字串表示大數。將大數用十進位制字元陣列表示，然後按照“豎式計算”的思想進行計算。這種方法比較容易理解，但是計算效率很低。

（2）將大數看成二進位制流進行處理。使用各種位運算和邏輯操作來實現大數的運算。該方法設計複雜，可讀性較差，而且難以除錯。

（3）將大數表示成一個n進位制陣列。n的取值越大，陣列的大小越小，這樣可以縮短運算的時間及空間複雜度，提高演算法的效率。在32位系統中，n可以取2^32，這時每一位的取值範圍是0~0xffffffff。

    這裡考慮用方法（3）來實現，當n=2^32時，大數的每一位恰好是unsigned long 的範圍，考慮到加法和乘法中進位時的溢位現象不好判斷，可以選取long long型，並且對於每個大數，包含一個變數表示其符號，一個變數來表示其長度，一個數組來儲存每一位的值。於是，可以用下面結構體表示一個大數：

typedef struct LargeNumber
{
    bool tag;                          // 標誌大數的符號 true：正數 ，false ：負數
    int length;                         // 記錄大數的長度
    long long bigInt[SIZE];              // 記錄大數各位的值
 
    LargeNumber( const bool& t=true,const int& len=0)
    {
        tag = t;
        length = len;
 
        for( int i=0; i<SIZE; ++i )
        {
            bigInt[i]= 0;
        }
    }
};
 

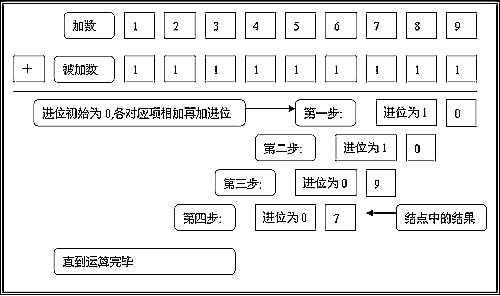
一、大數加法

   假設在加法中兩個運算元都是大於0的。按照“豎式計算”的思想，首先將兩運算元低位對齊，然後從最低位開始按“位”相加，當“位”相加的結果大於2^32-1時做進位處理（carry=1），否則不進位（carry=0）。

符號演示：op1=ABCD， op2=EFG

    A  B  C  D

    +  E  F  G

-------------------

H  I  J  K   L

   初始化carry=0，其中若D+G+carry>0xffffffff則L=D+G+carry-0xffffffff-1, carry=1；否則L=D+G+carry，carry=0，按照上述方法計算K,J,I,H。

例如：0x1  0x1  0x1  + 0xffffffff 0xffffffff; 初始carry=0

運算過程：

（1）0x1+0xffffffff+0>0xffffffff, 所以計算結果的最低位result.bigInt[0]=0x0,carry=1;

（2）0x1+0xffffffff+1>0xffffffff,所以result.bigInt[1]= 0x1+0xffffffff+1-0xffffffff-1=1,carry=1;

（3）0x1+1<0xffffffff,所以result.bigInt[2]=2;result.length=2;

最終結果為2  1  0

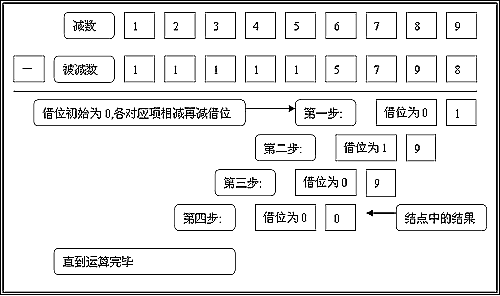
二、大數減法

   為了簡化計算，假設被減數總是不小於減數，這樣計算的最終結果總是大於等於0。基本思路和大數加法基本一致，減法中可能需要借位，定義並初始借位變數borrow=0。顯然，borrow要麼等於0，要麼等於1。

例如：0x1 0x1 0x1 – 0xffffffff  0xffffffff;初始borrow=0

計算過程：

(1) 0x1<0xfffffff+borrow,這時需要借位，result.bigInt[0]= 0xffffffff-(0xffffffff+0-0x1)+1=2,borrow=1;

(2)0x1<0xffffffff+borrow,於是result.bigInt[1]= 0xffffffff-(0xffffffff+1-0x1)+1=1,borrow=1;

(3)0x1=0+borrow,於是result.bigInt[2]=0, borrow=0;

最終結果為：1  2

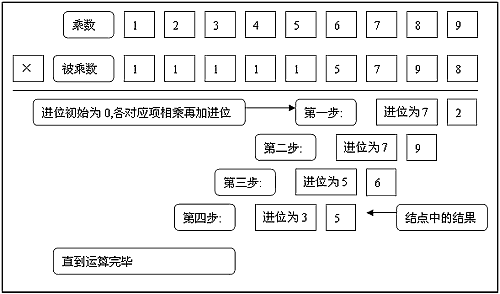
三、大數乘法

   假設乘法的兩個運算元均為正數。按照“豎式計算”的思想，大數的乘法可以藉助大數的加法，用乘數的每一位乘以被乘數，然後將每一次的計算結果相加。在每位相乘的過程中依然存在進位現象，而且此時進位不只是1，還存在更大的數。

過程演示：

        A   B

  *    C   D

---------------

       E  F G

+ H  I  J

----------------------------

K M N  O P

      其中，若B*D+carry>0xffffffff,那麼進位G=(B*D+carry)%0xffffffff，carry=(B*D+carry)/0xffffffff;

否則，G=B*D+carry,carry=0;按照上述計算原則計算,F E J I H.並按照大數加法的計算方法計算P O N M K。

例如： 0x1  0x1  0x1 * 0xffffffff  0xffffffff。

計算過程：

（1）0x1 0x1 0x1 * 0xffffffff =0xffffffff 0xffffffff 0xffffffff

（2）0x1 0x1 0x1 * 0xffffffff =0xffffffff 0xffffffff 0xffffffff,由於這是乘數的第一位，所以結果“擴充套件一位”，變成0xffffffff 0xffffffff 0xffffffff 0x0

（3）計算0xffffffff 0xffffffff 0xffffffff + 0xffffffff 0xffffffff 0xffffffff 0x0

（4）結果為1 0 0xffffffff 0xfffffffe 0xffffffff

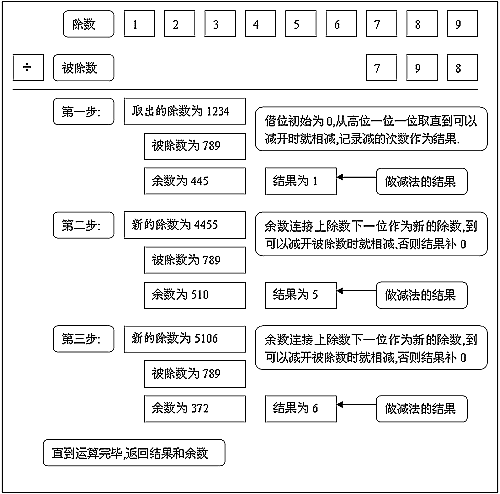
四、大數除法 

  除法建立在乘法的基礎上，迴圈搜尋num使得num*op1==op2，效率較低。

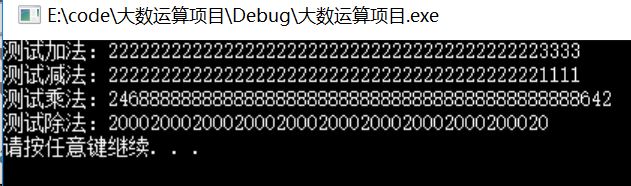
執行結果：