KL距離,Kullback-Leibler Divergence 淺談KL散度
KL距離,是Kullback-Leibler差異(Kullback-Leibler Divergence)的簡稱,也叫做相對熵(Relative Entropy)。它衡量的是相同事件空間裡的兩個概率分佈的差異情況。其物理意義是:在相同事件空間裡,概率分佈P(x)的事件空間,若用概率分佈Q(x)編碼時,平均每個基本事件(符號)編碼長度增加了多少位元。我們用D(P||Q)表示KL距離,計算公式如下:
當兩個概率分佈完全相同時,即P(x)=Q(X),其相對熵為0 。我們知道,概率分佈P(X)的資訊熵為:
其表示,概率分佈P(x)編碼時,平均每個基本事件(符號)至少需要多少位元編碼。通過資訊熵的學習,我們知道不存在其他比按照本身概率分佈更好的編碼方式了,所以D(P||Q)始終大於等於0的。雖然KL被稱為距離,但是其不滿足距離定義的三個條件:1)非負性;
我們以一個例子來說明,KL距離的含義。
假如一個字元發射器,隨機發出0和1兩種字元,真實發出概率分佈為A,但實際不知道A的具體分佈。現在通過觀察,得到概率分佈B與C。各個分佈的具體情況如下:
A(0)=1/2,A(1)=1/2
B(0)=1/4,B(1)=3/4
C(0)=1/8,C(1)=7/8
那麼,我們可以計算出得到如下:
也即,這兩種方式來進行編碼,其結果都使得平均編碼長度增加了。我們也可以看出,按照概率分佈B進行編碼,要比按照C進行編碼,平均每個符號增加的位元數目少。從分佈上也可以看出,實際上B要比C更接近實際分佈。
如果實際分佈為C,而我們用A分佈來編碼這個字元發射器的每個字元,那麼同樣我們可以得到如下:
再次,我們進一步驗證了這樣的結論:對一個資訊源編碼,按照其本身的概率分佈進行編碼,每個字元的平均位元數目最少。這就是資訊熵的概念,衡量了資訊源本身的不確定性。另外,可以看出KL距離不滿足對稱性,即D(P||Q)不一定等於D(Q||P)。
當然,我們也可以驗證KL距離不滿足三角不等式條件。
上面的三個概率分佈,D(B||C)=1/4log2+3/4log(6/7)。可以得到:D(A||C) - (D(A||B)+ D(B||C)) =1/2log2+1/4log(7/6)>0,這裡驗證了KL距離不滿足三角不等式條件。所以KL距離,並不是一種距離度量方式,雖然它有這樣的學名。
其實,KL距離在資訊檢索領域,以及統計自然語言方面有重要的運用。我們將會把它留在以後的章節中介紹。
利用資訊理論的方法可以進行一些簡單的自然語言處理
比如利用相對熵進行分類或者是利用相對熵來衡量兩個隨機分佈的差距,當兩個隨機分佈相同時,其相對熵為0.當兩個隨機分佈的差別增加時,器相對熵也增加。我們下面的實驗是為了橫量概率分佈的差異。
試驗方法、要求和材料
要求:
1.任意摘錄一段文字,統計這段文字中所有字元的相對頻率。假設這些相對頻率就是這些字元的概率(即用相對頻率代替概率);
2.另取一段文字,按同樣方法計算字元分佈概率;
3.計算兩段文字中字元分佈的KL距離;
4.舉例說明(任意找兩個分佈p和q),KL距離是不對稱的,即D(p//q)!=D(q//p);
方法:
D(p//q)=sum(p(x)*log(p(x)/q(x)))。其中p(x)和q(x)為兩個概率分佈
約定 0*log(0/q(x))=0;p(x)*log(p(x)/0)=infinity;
一、第一種理解
相對熵(relative entropy)又稱為KL散度(Kullback–Leibler divergence,簡稱KLD),資訊散度(information divergence),資訊增益(information gain)。
KL散度是兩個概率分佈P和Q差別的非對稱性的度量。
KL散度是用來度量使用基於Q的編碼來編碼來自P的樣本平均所需的額外的位元個數。 典型情況下,P表示資料的真實分佈,Q表示資料的理論分佈,模型分佈,或P的近似分佈。
根據shannon的資訊理論,給定一個字符集的概率分佈,我們可以設計一種編碼,使得表示該字符集組成的字串平均需要的位元數最少。假設這個字符集是X,對x∈X,其出現概率為P(x),那麼其最優編碼平均需要的位元數等於這個字符集的熵:
H(X)=∑x∈XP(x)log[1/P(x)]
在同樣的字符集上,假設存在另一個概率分佈Q(X)。如果用概率分佈P(X)的最優編碼(即字元x的編碼長度等於log[1/P(x)]),來為符合分佈Q(X)的字元編碼,那麼表示這些字元就會比理想情況多用一些位元數。KL-divergence就是用來衡量這種情況下平均每個字元多用的位元數,因此可以用來衡量兩個分佈的距離。即:
DKL(Q||P)=∑x∈XQ(x)[log(1/P(x))] - ∑x∈XQ(x)[log[1/Q(x)]]=∑x∈XQ(x)log[Q(x)/P(x)]
由於-log(u)是凸函式,因此有下面的不等式
DKL(Q||P) = -∑x∈XQ(x)log[P(x)/Q(x)] = E[-logP(x)/Q(x)] ≥ -logE[P(x)/Q(x)] = - log∑x∈XQ(x)P(x)/Q(x) = 0
即KL-divergence始終是大於等於0的。當且僅當兩分佈相同時,KL-divergence等於0。
===========================
舉一個實際的例子吧:比如有四個類別,一個方法A得到四個類別的概率分別是0.1,0.2,0.3,0.4。另一種方法B(或者說是事實情況)是得到四個類別的概率分別是0.4,0.3,0.2,0.1,那麼這兩個分佈的KL-Distance(A,B)=0.1*log(0.1/0.4)+0.2*log(0.2/0.3)+0.3*log(0.3/0.2)+0.4*log(0.4/0.1)
這個裡面有正的,有負的,可以證明KL-Distance()>=0.
從上面可以看出, KL散度是不對稱的。即KL-Distance(A,B)!=KL-Distance(B,A)
KL散度是不對稱的,當然,如果希望把它變對稱,
Ds(p1, p2) = [D(p1, p2) + D(p2, p1)] / 2.
二、第二種理解
今天開始來講相對熵,我們知道資訊熵反應了一個系統的有序化程度,一個系統越是有序,那麼它的資訊熵就越低,反之就越高。下面是熵的定義
如果一個隨機變數 的可能取值為
的可能取值為 ,對應的概率為
,對應的概率為 ,則隨機變量
,則隨機變量 的熵定義為
的熵定義為

有了資訊熵的定義,接下來開始學習相對熵。
1. 相對熵的認識
相對熵又稱互熵,交叉熵,鑑別資訊,Kullback熵,Kullback-Leible散度(即KL散度)等。設 和
和
是 取值的兩個概率概率分佈,則
取值的兩個概率概率分佈,則 對
對 的相對熵為
的相對熵為

在一定程度上,熵可以度量兩個隨機變數的距離。KL散度是兩個概率分佈P和Q差別的非對稱性的度量。KL散度是
用來度量使用基於Q的編碼來編碼來自P的樣本平均所需的額外的位元數。 典型情況下,P表示資料的真實分佈,Q
表示資料的理論分佈,模型分佈,或P的近似分佈。
2. 相對熵的性質
相對熵(KL散度)有兩個主要的性質。如下
(1)儘管KL散度從直觀上是個度量或距離函式,但它並不是一個真正的度量或者距離,因為它不具有對稱性,即

(2)相對熵的值為非負值,即

在證明之前,需要認識一個重要的不等式,叫做吉布斯不等式。內容如下

3. 相對熵的應用
相對熵可以衡量兩個隨機分佈之間的距離,當兩個隨機分佈相同時,它們的相對熵為零,當兩個隨機分佈的差別增大時,它們的相對熵也會增大。所以相對熵(KL散度)可以用於比較文字的相似度,先統計出詞的頻率,然後計算
KL散度就行了。另外,在多指標系統評估中,指標權重分配是一個重點和難點,通過相對熵可以處理。
三、用在CF中
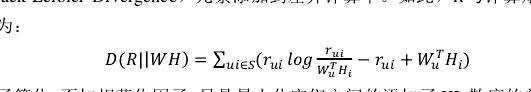
第一,KLD需要概率(臉頰和1),但是用評分。
第二,後面兩項的作用。

