生成樹：由圖生成的樹，由圖轉化為樹，進一步可用對樹的相關操作來對圖進行操作。最小指的是權值最小；

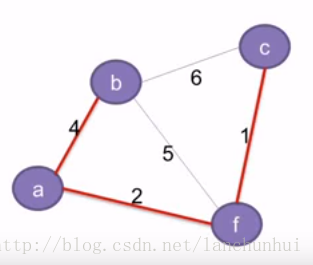
• 生成樹是邊的集合，如下圖所示的最小生成樹：MST={{a,b},{a,f},{f,c}}

  
  
  

本文主要探討帶權無向連通圖（網路）上的最小生成樹問題，以及求最小生成樹的兩個演算法。

0. 生成數

• n 個頂點的圖，有 n−1 棵生成樹；

1. 最小生成樹

最小生成樹有很多實際應用。例如，將網路頂點看做城市，邊看做連線城市的通訊網，邊的權看做連線城市的通訊線路的成本，根據最小生成樹建立的通訊網就是這些城市之間成本最低的通訊網。

2. Kruskal 演算法

3. Prim 演算法

Prim 演算法的設計出發點與 Kruskal 演算法完全不同：

• Prim 演算法從一個頂點出發，逐步擴充包含該頂點的部分生成樹 T；

Prim 演算法的實施，需要用到關於最小生成樹的一個重要特性，描述如下：

設 G=(V,E) 是一個網路，U 是 V 的任一真子集，設 e=(u,v)∈E，且u∈U,v∈V−U（也就是說，e 的一個端點在 U 裡，另一個不在），且 e 在 G 中所有一個端點在 U 而另一個端點在 V−U 的邊中權值最小，那麼 G 中必有一棵包含邊 e 的最小生成樹。