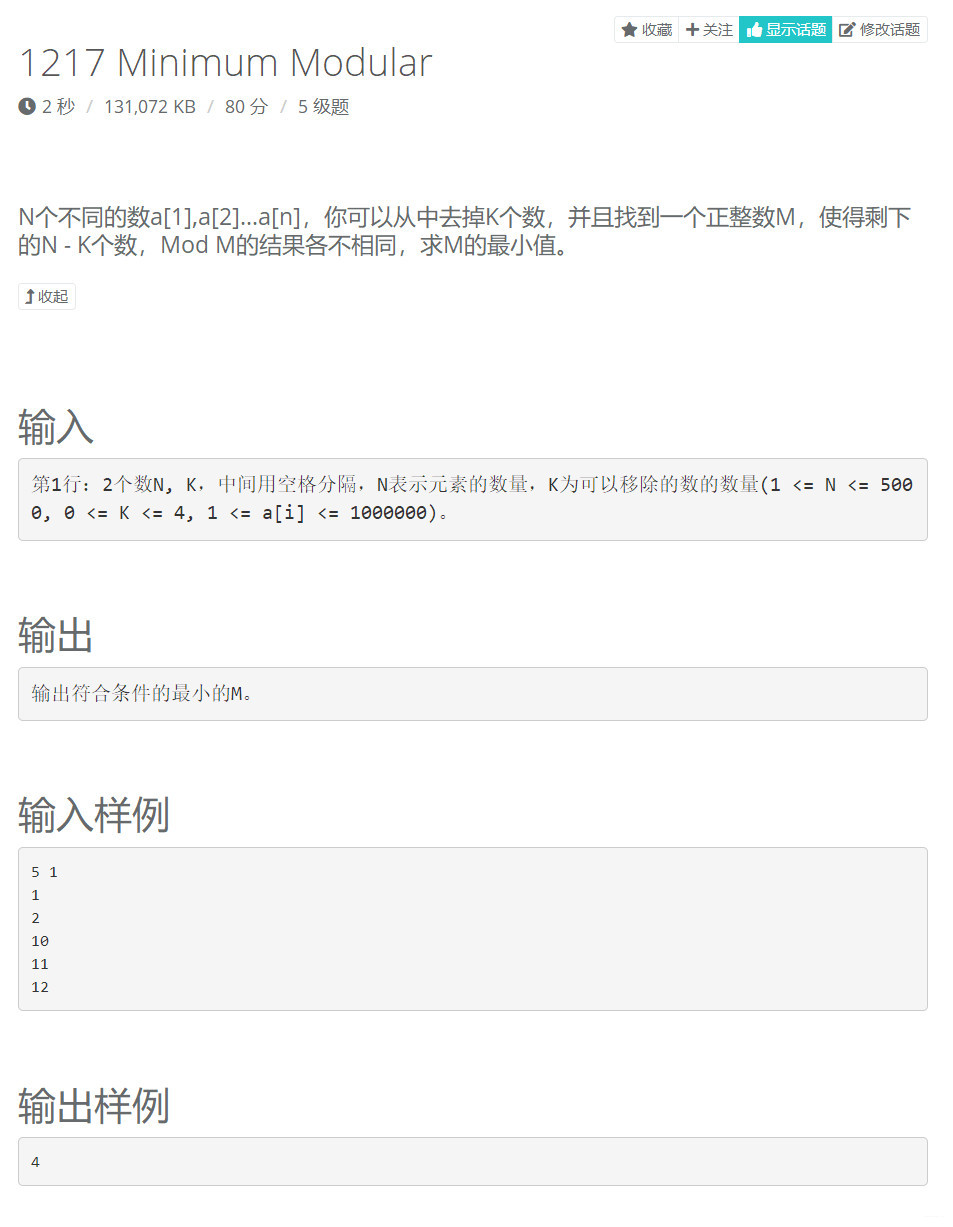
【題目描述】

【思路】
這個題我們可以考慮從小到大列舉m（從max(1,n-k)到max(a[i])+1），然後判斷能否在刪不超過k個數的情況下滿足每個數模m都互不相同。

對於模m的情況，a[i]≡a[j](mod m)當且僅當a[i]-a[j]是m的倍數，我們可以先預處理出a[i]-a[j]=w的個數cnt[w]，然後對於模m的情況，就只用考慮刪m|a[i]-a[j]的i或j了，根據調和級數我們可以算出列舉1_{p裡每個數在1}p裡的倍數的時間複雜度是O(plogp)的，對於此題，p<=10^6+1，可以承受。
而k個模m同餘的數最多可可以形成k*(k+1)/2對同餘二元組(i,j)，所以對於每個m，我們可以算出滿足m|w的cnt[w]之和，如果超過k*(k+1)/2就可以直接確定這個m不可行。否則就暴力計算模m是否可行。

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;

const int maxa=1000005;
const int maxn=5005;

int n,k;
int a[maxn],num[maxa];
bool used[maxa];

int main(){
    scanf("%d%d",&n,&k);
    for(int i=0;i<n;++i) scanf("%d",&a[i]);
    sort(a,a+n);
    for(int i=0;i<n;++i){
        for(int j=i+1;j<n;++j){
            ++num[a[j]-a[i]];
        }
    }
    int m=n-k;
    while(1){
        int cnt=0;
        for(int i=m;i<maxa;i+=m) cnt+=num[i];
        if(cnt>(k+1)*k/2){
            ++m;
            continue;
        }
        cnt=0;
        for(int i=0;i<m;++i) used[i]=false;
        for(int i=0;i<n;++i){
            int x=a[i]%m;
            if(used[x]) ++cnt;
            used[x]=true;
        }
        if(cnt<=k) break;
        else ++m;
    }
    printf("%d\n",m);
    return 0;
}