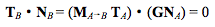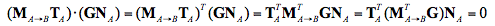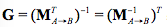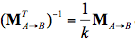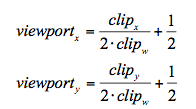本系列文章由Aimar_Johnny編寫，歡迎轉載，轉載請標明出處，謝謝。

http://blog.csdn.net/lzhq1982/article/details/73747162

前兩篇介紹了Unity Shader的主要數學部分，書上還有些相關的數學介紹，將在這篇做最後的總結。

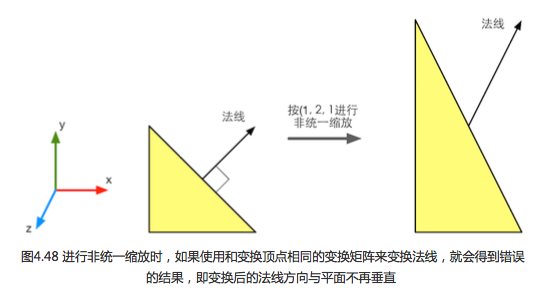
1、法線變換

法線（normal），也被稱為法向量。遊戲中，模型的頂點攜帶的資訊中，法線就是其中一種。我們變換一個模型，不僅需要變換它的頂點，還需要變換頂點法線，以便在後續處理中計算光照等。

從上一篇我們知道，點和大部分方向向量都可以用同一個變換矩陣在兩個空間之間變換。但法線用同一個變換矩陣，可能無法確保維持法線的垂直性。下面介紹一下原因。

先來了解一下另一種方向向量：切線（tangent），也叫切向量。也是頂點攜帶的一種資訊。它與法線方向垂直。切線是兩個點之間的差值計算得來的，因此可以直接用變換頂點的變換矩陣來變換切線。假設，這個變換頂點也就是變換切線的矩陣是3x3的變換矩陣 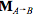（因為是方向向量，不受平移影響，不用4x4），得到空間變換公式如下：

T表示切線，上面表示切線從空間A到空間B的轉換。但如果直接用同一矩陣變換法線，得到的新法線可能就不會與表面垂直了，例如：

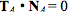
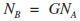
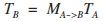
那麼怎麼求法線變換的矩陣呢。答案是用法線和切線垂直的約束公式：。假設我們用矩陣G來變換法線，則有。然後結合，我們得到下面公式：

然後推導可得：

有很多人對第一個等式有疑問，請大家注意第一個等式左邊是向量點乘，有個點，等式右邊把向量變成了列矩陣，變成了矩陣相乘，中間沒點了。其他應該沒問題。看最後的等式部分，因為

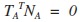，把T變成列矩陣，所以，所以如果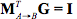，那麼上面的等式就成立了。那我們的結論就是：

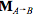
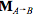
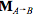
如果是正交矩陣，那其逆就是其轉置，那麼G = ，也就是說我們可以用變換頂點的矩陣變換法線。從上一篇的表格中可以看出，旋轉變換是正交矩陣，可以直接用，如果只包含旋轉和統一縮放，不包含非統一縮放，則

其他情況，我們就要求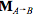的逆轉置了。

2、Unity Shader 內建變數（數學）

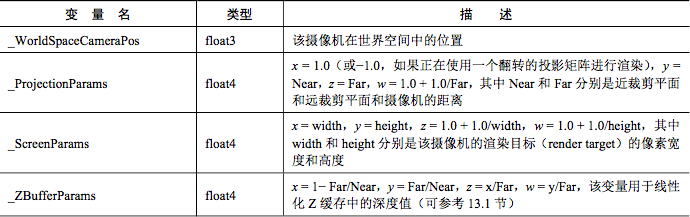
Unity給我們提供了很多有關變換的內建引數，這些內建變數可以在UnityShaderVariables.cginc檔案中找到定義和說明。

1）變換矩陣

注意最後兩個，Unity5.5版本中_Object2World已經變成unity_ObjectToWorld，_World2Object也變成了unity_WorldToObject，但由於Unity的向下相容性，Unity會自動改寫它們，不會出錯。還有在頂點著色器中，我們往往第一行就會用到UNITY_MATRIX_MVP：mul(UNITY_MATRIX_MVP, v.vertex); 這是把頂點從模型空間轉換到裁剪空間，不用我們手動變換空間了，不過這在unity5.6中已經改為：UnityObjectToClipPos(v.vertex); 在UnityShaderUtilities.cginc裡，注意5.6以上版本才有這個檔案。官方實現如下：

// Tranforms position from object to homogenous space
inline float4 UnityObjectToClipPos(in float3 pos)
{
    // More efficient than computing M*VP matrix product
    return mul(UNITY_MATRIX_VP, mul(unity_ObjectToWorld, float4(pos, 1.0)));
}

可以看出也是先轉到世界空間，再乘以觀察和投影矩陣，只不過註釋那裡很清楚，更高效一些。

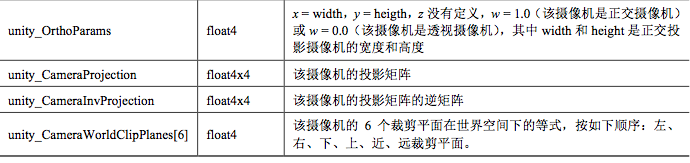
2）攝像機和螢幕引數

讀者也沒有必要記住他們，以後用到了方便查閱就行。用多了就記住了。

3、Cg中向量和矩陣型別

我在Unity Shader基礎裡說過Cg，是我們目前主要的著色器程式語言。這裡主要說一下Cg中向量和矩陣的表達方式。Cg中，矩陣是由float3x3、float4x4等關鍵字定義的，向量是由float3、float4等關鍵字定義的，當然，也可以當成是1xn行矩陣或nx1的列矩陣，這取決於運算種類和運算中的位置。如下：

float4 a = float4(1.0, 2.0, 3.0, 4.0);

float4 b = float4(1.0, 2.0, 3.0, 4.0);

點積：float result = dot(a, b);

但在矩陣乘法時，引數位置決定是按行矩陣還是列矩陣進行乘法。Cg中矩陣乘法的函式是mul。

float4 v = float4(1.0, 2.0, 3.0, 4.0);
float4x4 M = float4x4(1.0, 0.0, 0.0, 0.0,
				0.0, 2.0, 0.0, 0.0,
				0.0, 0.0, 3.0, 0.0,
				0.0, 0.0, 0.0, 4.0);
//v當成列矩陣和矩陣M右乘
float4 column_mul = mul(M, v);

//v當成行矩陣左乘
float4 row_mul = mul(v, M);

//注意：column_mul 不等於 row_mul，而是：
//mul(M, v) = mul(v, tranpose(M));
//mul(v, M) = mul(tranpose(M), v);

從上面可以看出，向量、矩陣的位置會影響結果值。通常在變換頂點時，我們用右乘列矩陣的方式。有時也用左乘，省去矩陣轉置的操作。

4、Unity螢幕座標：ComputeScreenPos/VPOS/WPOS
這塊內容是有點超前的，只不過涉及數學計算部分，所以放在這裡，請大家記住有這麼回事，後面螢幕抓取那裡我們會用到ComputeGrabScreenPos，到時候還需要你回來看。好了，進入主題。

在寫shader時，我們有時希望獲得片元在螢幕上的畫素位置。在頂點/片元著色器中，有兩種方式獲得片元的螢幕座標。

1）在片元著色器的輸入中宣告VPOS或WPOS語義（語義以後再講）。

VPOS是HLSL中對螢幕座標的語義，WPOS是Cg中對螢幕座標的語義。兩者在Unity Shader中是等價的。我們可以在HLSL/Cg中通過語義的方式定義頂點/片元著色器的預設輸入，不用自己定義輸入輸出的資料結構。如是我們可以在片元著色器中這樣寫：

fixed4 frag(float4 sp : VPOS) : SV_Target {
    //用螢幕座標除以螢幕解析度_ScreenParams.xy，得到視口空間中的座標
    return fixed4(sp.xy/_ScreenParams.xy, 0.0, 1.0);
}

這裡是把螢幕座標轉化成顏色值輸出了，這是典型的用顏色值驗證結果的方法，因為shader沒法除錯，那用顏色值輸出可以直觀的驗證我們的結論。VPOS/WPOS是一個float4的變數，xy代表了螢幕空間的畫素座標。如果螢幕解析度是400*300，x的範圍是[0.5, 400.5]，y的範圍是[0.5, 300.5]，這裡的畫素座標不是整數值，因為OpenGL和DirectX 10以後的版本認為畫素中心對應的是0.5。所以sp.xy/_ScreenParams.xy的結果就是(0, 0)到(1, 1)，所以左下角是黑色，右上角是黃色，結果如圖：

我們用了VPOS/WPOS的xy，那zw呢，在Unity中，它們的z分量範圍是[0, 1]，攝像機近裁剪面z為0，遠裁剪面z為1。w分量取決於投影型別，透視投影w範圍是[1/Near, 1/Far]，Near和Far對應了Camera元件中設定的近裁剪平面和遠裁剪平面距離攝像機的遠近。正交投影w值恆為1。

2）通過Unity提供的ComputeScreenPos函式

這個函式在UnityCG.cginc裡被定義。直接上程式碼：

struct vertOut {
	float4 pos : SV_POSITION;
	float4 srcPos : TEXCOORD0;
}

vertOut vert (appdata_base v) {
	vertOut o;
	o.pos = mul (UNITY_MATRIX_MVP, v.vertex);
	//第一步：把ComputeScreenPos的結果儲存在srcPos中
	o.srcPos = ComputeScreenPos(o.pos);
	return o;
}

fixed4 frag (vertOut i) : SV_Target {
	//第二步：用srcPos.xy除以srcPos.w得到視口空間中的座標
	float2 wcoord = i.srcPos.xy / i.srcPos.w;
	return fixed4(wcoord, 0.0, 1.0);
}

上面程式碼的實現效果和第一種效果一致。從上面程式碼可以看出，我們用了兩步獲得視口空間的座標，第一步在頂點著色器中用ComputeScreenPos函式計算的結果存在輸出結構體中，第二步在片元著色器中對傳過來的值進行了齊次除法得到視口空間的座標。下面我們分析一下：

上一篇我們看到了如何將裁剪空間中的點對映到螢幕空間中。這裡回憶一下，經過齊次除法後，我們把裁剪空間變換到了NDC中，不記得NDC的回頭看看，NDC的xy座標是[-1, 1]，而螢幕空間是[0, 1]，所以只要經過(x + 1) / 2的操作就可以對映過去了，所以我們得到如下公式：

這裡的clip的xy都是裁剪空間的，所以除以w變成NDC下，我們再看一下ComputeScreenPos的實現（unity5.6版本）：

inline float4 ComputeNonStereoScreenPos(float4 pos) {
    float4 o = pos * 0.5f;
    o.xy = float2(o.x, o.y*_ProjectionParams.x) + o.w;
    o.zw = pos.zw;
    return o;
}

inline float4 ComputeScreenPos(float4 pos) {
    float4 o = ComputeNonStereoScreenPos(pos);
#if defined(UNITY_SINGLE_PASS_STEREO)
    o.xy = TransformStereoScreenSpaceTex(o.xy, pos.w);
#endif
    return o;
}

ComputeScreenPos輸入的引數pos是經過MVP變換後的在裁剪空間的頂點座標。UNITY_SINGLE_PASS_STEREO我們先不考慮，貌似是給vr用的。所以核心部分在ComputeNonStereoScreenPos這裡，_ProjectionParams.x預設情況是1（如果使用了一個翻轉的投影矩陣的話是-1，很少見）。那這段程式碼輸出值o的各個分量是：
o.x = pos.x / 2 + pos.w / 2;

o.y = pos.y / 2 + pos.w / 2;

o.z = pos.z;

o.w = pos.w;

讀者可以看出，o.x和o.y並不是視口空間的座標，除以pos.w就和上面等式相同了，所以我們看片元著色器中的第二步就是這個操作。但為什麼不在頂點著色器裡的ComputeScreenPos裡直接除卻要在片元著色器中除呢，這是因為如果在頂點著色器中除的話，會破壞插值結果。從頂點著色器到片元著色器會有個插值的過程，這點在渲染流水線中說過了。如果我們對x/w，y/w進行插值，結果會不準確。因為投影空間不是線性空間，插值往往是線性的，所以不要在投影空間進行插值。最後我們看輸出的zw沒變化，還是裁剪空間的zw，所以如果使用透視投影，z範圍是[-Near, Far]，w範圍是[Near, Far]（讀者忘了可以看上一篇的裁剪空間圖）。如果是正交投影，z是[-1, 1]，w是1。

最後比書上多說一點是ComputeGrabScreenPos，後面抓取螢幕中會遇到，再過來看看。我們直接看看程式碼：

inline float4 ComputeGrabScreenPos (float4 pos) {
    #if UNITY_UV_STARTS_AT_TOP
    float scale = -1.0;
    #else
    float scale = 1.0;
    #endif
    float4 o = pos * 0.5f;
    o.xy = float2(o.x, o.y*scale) + o.w;
#ifdef UNITY_SINGLE_PASS_STEREO
    o.xy = TransformStereoScreenSpaceTex(o.xy, pos.w);
#endif
    o.zw = pos.zw;
    return o;
}

你會發現除了UNITY_UV_STARTS_AT_TOP這個巨集判斷，基本沒啥變化，這個巨集後面會常遇到，OpenGL是左下角為原點，DirectX是左上角為原點，所以如果是左上角為原點，那y要取反，就這點區別。

數學部分的介紹到此結束，但Shader離不開數學運算，書裡推薦了擴充套件閱讀，有興趣的就多多研究吧。

（最後感嘆一下女神這個章節的書寫，我用三篇分開整理，內容還這麼龐大，編輯公式好麻煩啊！！！）