資訊熵與資訊增益（IE, Information Entropy; IG, Information Gain）

資訊增益是機器學習中特徵選擇的關鍵指標，而學習資訊增益前，需要先了解資訊熵和條件熵這兩個重要概念。

資訊熵（資訊量）

資訊熵的意思就是一個變數i（就是這裡的類別）可能的變化越多（只和值的種類多少以及發生概率有關，反而跟變數具體的取值沒有任何關係），它攜帶的資訊量就越大（因為是相加累計），這裡就是類別變數i的資訊熵越大。

系統越是有序，資訊熵就越低；反之，一個系統越亂，資訊熵就越高。所以，資訊熵也可以說是系統有序化程度的一個衡量。

二分類問題中，當X的概率P(X)為0.5時，也就是表示變數的不確定性最大，此時的熵也達到最大值1。

條件熵

條件熵的直觀理解：單獨計算明天下雨的資訊熵H(Y)是2，而條件熵H（Y|X）是0.01（即今天陰天這個條件下，明天下雨的概率很大，確定性很大，資訊量就很少），這樣相減後為1.99，在獲得陰天這個資訊後，下雨資訊不確定性減少了1.99！是很多的！所以資訊增益大！所以是否陰天這個特徵資訊X對明天下雨這個隨機變數Y的來說是很重要的！

因為條件熵中X也是一個變數，意思是在一個變數X的條件下（變數X的每個值都會取），另一個變數Y熵對X的期望，這裡的期望就是指所有情況各自概率的∑總和。

在文字分類中，特徵詞t的取值只有t（代表t出現）和（代表t不出現）。那麼系統熵等於兩種條件熵按比例求和：

示例說明條件熵

設樣品房資料集樣本12份，變數Y為房屋價格，根據價格計算該資料集的夏農熵（即資訊熵），其中價格高的4個佔1/3，價格中等的6個佔1/2，價格低的2個佔1/6，其夏農熵為：

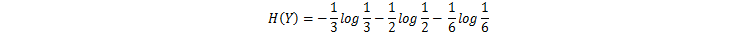
如圖，在房屋的面積X這個條件下計算價格Y的條件熵，根據面積X，面積大的4個（價格3高1中）設為a，面積中的3個（價格3中）設為b，面積小的5個（價格1高2中2低）設為c，先分別計算a,b,c條件下的資訊熵為：

再計算a,b,c資訊熵的按比例求和，便得到在條件X條件下，Y的條件熵為：

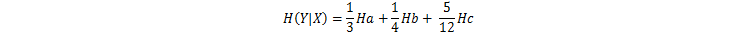
資訊增益

評價一個系統的特徵t對系統的影響程度就要用到條件熵，即是特徵t存在和不存在的條件下，系統的類別變數i的資訊熵。特徵t條件下的資訊熵與原始資訊熵的差值就是這個特徵給系統帶來的資訊增益。

資訊增益最大的問題還在於它只能考察特徵對整個系統的貢獻，而不能具體到某個類別上，這就使得它只適合用來做所謂“全域性”的特徵選擇（指所有的類都使用相同的特徵集合），而無法做“本地”的特徵選擇（每個類別有自己的特徵集合，因為有的詞，對這個類別很有區分度，對另一個類別則無足輕重）。

附：特徵提取步驟

1. 卡方檢驗

1.1  統計樣本集中文件總數（N）。

1.2  統計每個詞的正文件出現頻率（A）、負文件出現頻率（B）、正文件不出現頻率（C）、負文件不出現頻率（D）。

1.3 計算每個詞的卡方值，公式如下：

1.4  將每個詞按卡方值從大到小排序，選取前k個詞作為特徵，k即特徵維數。

2. 資訊增益

2.1  統計正負分類的文件數:N1、N2。

2.2  統計每個詞的正文件出現頻率（A）、負文件出現頻率（B）、正文件不出現頻率）、負文件不出現頻率。

2.3  計算資訊熵

2.4  計算每個詞的資訊增益

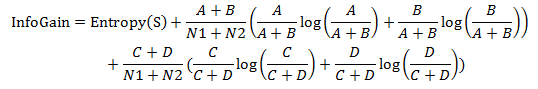
2.5  將每個詞按資訊增益值從大到小排序，選取前k個詞作為特徵，k即特徵維數。