十分鐘上手sklearn:特徵提取,常用模型,交叉驗證
這一篇雖然叫做:十分鐘上手sklearn:特徵提取,常用模型,但是寫著寫著我就想把每一個模型都詳細說一下,所以也可以看作是機器學習演算法概述了。
上一篇我們講解了如何安裝sklearn,匯入自帶資料集,建立資料,對資料進行預處理,通過上一篇的講解,相信大家能夠感受到sklearn的強大之處。
這一篇,我們將對sklearn中有關特徵提取,常用模型進行講解。
主要內容包括:
1.PCA演算法
2.LDA演算法
3.線性迴歸
4.邏輯迴歸
5.樸素貝葉斯
6.決策樹
7.SVM
8.神經網路
9.KNN演算法
是不是感覺乾貨滿滿啊!Let’s get moving!!!
特徵提取
我們獲取的資料中很多資料往往有很多維度,但並不是所有的維度都是有用的,有意義的,所以我們要將對結果影響較小的維度捨去,保留對結果影響較大的維度。
PCA(主成分分析)與LDA(線性評價分析)是特徵提取的兩種經典演算法。PCA與LDA本質上都是學習一個投影矩陣,使樣本在新的座標系上的表示具有相應的特性,樣本在新座標系的座標相當於新的特徵,保留下的新特徵應當是對結果有較大影響的特徵。
PCA(主成分分析)
最大方差理論:訊號具有較大的方差,噪聲具有較小的方差
PCA的目標:新座標系上資料的方差越大越好
PCA是無監督的學習方法
PCA實現起來並不複雜(過幾天寫一篇使用NumPy實現的PCA),但是在sklearn就更為簡單了,直接食用skleran.decomposition即可
import sklearn.decomposition as sk_decomposition
pca = sk_decomposition.PCA(n_components='mle',whiten=False,svd_solver='auto')
pca.fit(iris_X)
reduced_X = pca.transform(iris_X) #reduced_X為降維後的資料
print('PCA:')
print ('降維後的各主成分的方差值佔總方差值的比例',pca.explained_variance_ratio_)
print ('降維後的各主成分的方差值',pca.explained_variance_)
print 引數說明:
n_components:指定希望PCA降維後的特徵維度數目(>1), 指定主成分的方差和所佔的最小比例閾值(0-1),’mle’用MLE演算法根據特徵的方差分佈情況自己去選擇一定數量的主成分特徵來降維
whiten: 判斷是否進行白化。白化:降維後的資料的每個特徵進行歸一化,讓方差都為1
svd_solver:奇異值分解SVD的方法{‘auto’, ‘full’, ‘arpack’, ‘randomized’}
列印結果:
下面列印的內容只是幫助大家理解pca的引數,就不列印降維後的資料了,打印出來並沒有什麼意義。
PCA:
降維後的各主成分的方差值佔總方差值的比例 [ 0.92461621 0.05301557 0.01718514]
降維後的各主成分的方差值 [ 4.22484077 0.24224357 0.07852391]
降維後的特徵數 3LDA(線性評價分析)
LDA基於費舍爾準則,即同一類樣本儘可能聚合在一起,不同類樣本應該儘量擴散;或者說,同雷洋被具有較好的聚合度,類別間具有較好的擴散度。
既然涉及到了類別,那麼LDA肯定是一個有監督演算法,其實LDA既可以做特徵提取液可以做分類。
LDA具體的實現流程這裡就不再贅述了,直接看skleran如何實現LDA。
import sklearn.discriminant_analysis as sk_discriminant_analysis
lda = sk_discriminant_analysis.LinearDiscriminantAnalysis(n_components=2)
lda.fit(iris_X,iris_y)
reduced_X = lda.transform(iris_X) #reduced_X為降維後的資料
print('LDA:')
print ('LDA的資料中心點:',lda.means_) #中心點
print ('LDA做分類時的正確率:',lda.score(X_test, y_test)) #score是指分類的正確率
print ('LDA降維後特徵空間的類中心:',lda.scalings_) #降維後特徵空間的類中心引數說明:
n_components:指定希望PCA降維後的特徵維度數目(>1)
svd_solver:奇異值分解SVD的方法{‘auto’, ‘full’, ‘arpack’, ‘randomized’}
列印結果:
下面列印的內容只是幫助大家理解lda的引數,就不列印降維後的資料了,打印出來並沒有什麼意義。
LDA:
LDA的資料中心點:
[[ 5.006 3.418 1.464 0.244]
[ 5.936 2.77 4.26 1.326]
[ 6.588 2.974 5.552 2.026]]
LDA做分類時的正確率: 0.980952380952
LDA降維後特徵空間的類中心:
[[-0.81926852 0.03285975]
[-1.5478732 2.15471106]
[ 2.18494056 -0.93024679]
[ 2.85385002 2.8060046 ]]常用模型
好了,好了,終於可以開始講模型了,其實這才是我想講的重點啊,沒想到前面的內容都講了這麼多。。。
機器學習常用的演算法也就那幾個,sklearn中對其都做了實現,我們只需要呼叫即可。下面每一個演算法的原理我就不細講了,只講怎麼用,以後會寫這些演算法的具體原理與實現方式。
乾貨要來了,準備好!
首先sklearn中所有的模型都有四個固定且常用的方法,其實在PCA與LDA中我們已經用到了這些方法中的fit方法。
# 擬合模型
model.fit(X_train, y_train)
# 模型預測
model.predict(X_test)
# 獲得這個模型的引數
model.get_params()
# 為模型進行打分
model.score(data_X, data_y) # 迴歸問題:以R2引數為標準 分類問題:以準確率為標準線性迴歸
線性迴歸是利用數理統計中迴歸分析,來確定兩種或兩種以上變數間相互依賴的定量關係的一種統計分析方法,運用十分廣泛。其表達形式為y = w’x+e,e為誤差服從均值為0的正態分佈。
迴歸分析中,只包括一個自變數和一個因變數,且二者的關係可用一條直線近似表示,這種迴歸分析稱為一元線性迴歸分析。如果迴歸分析中包括兩個或兩個以上的自變數,且因變數和自變數之間是線性關係,則稱為多元線性迴歸分析。
其實,說白了,就是用一條直線去擬合一大堆資料,最後把係數w和截距b算出來,直線也就算出來了, 就可以拿去做預測了。
sklearn中線性迴歸使用最小二乘法實現,使用起來非常簡單。
線性迴歸是迴歸問題,score使用R2係數做為評價標準。
import sklearn.linear_model as sk_linear
model = sk_linear.LinearRegression(fit_intercept=True,normalize=False,copy_X=True,n_jobs=1)
model.fit(X_train,y_train)
acc=model.score(X_test,y_test) #返回預測的確定係數R2
print('線性迴歸:')
print('截距:',model.intercept_) #輸出截距
print('係數:',model.coef_) #輸出係數
print('線性迴歸模型評價:',acc)引數說明:
fit_intercept:是否計算截距。False-模型沒有截距
normalize: 當fit_intercept設定為False時,該引數將被忽略。 如果為真,則迴歸前的迴歸係數X將通過減去平均值併除以l2-範數而歸一化。
copy_X:是否對X陣列進行復制,預設為True
n_jobs:指定執行緒數
列印結果:
線性迴歸:
截距: -0.379953866745
係數: [-0.02744885 0.01662843 0.17780211 0.65838886]
線性迴歸模型評價: 0.913431360638邏輯迴歸
logistic迴歸是一種廣義線性迴歸(generalized linear model),因此與多重線性迴歸分析有很多相同之處。它們的模型形式基本上相同,都具有 w‘x+b,其中w和b是待求引數,其區別在於他們的因變數不同,多重線性迴歸直接將w‘x+b作為因變數,即y =w‘x+b,而logistic迴歸則通過函式L將w‘x+b對應一個隱狀態p,p =L(w‘x+b),然後根據p 與1-p的大小決定因變數的值。如果L是logistic函式,就是logistic迴歸,如果L是多項式函式就是多項式迴歸。
說人話:線性迴歸是迴歸,邏輯迴歸是分類。邏輯迴歸通過logistic函式算概率,然後算出來一個樣本屬於一個類別的概率,概率越大越可能是這個類的樣本。
sklearn對於邏輯迴歸的實現也非常簡單,直接上程式碼了。
邏輯迴歸是分類問題,score使用準確率做為評價標準。
import sklearn.linear_model as sk_linear
model = sk_linear.LogisticRegression(penalty='l2',dual=False,C=1.0,n_jobs=1,random_state=20,fit_intercept=True)
model.fit(X_train,y_train) #對模型進行訓練
acc=model.score(X_test,y_test) #根據給定資料與標籤返回正確率的均值
print('邏輯迴歸模型評價:',acc)引數說明:
penalty:使用指定正則化項(預設:l2)
dual: n_samples > n_features取False(預設)
C:正則化強度的反,值越小正則化強度越大
n_jobs: 指定執行緒數
random_state:隨機數生成器
fit_intercept: 是否需要常量
列印結果:
邏輯迴歸模型評價: 0.8 樸素貝葉斯
貝葉斯分類是一類分類演算法的總稱,這類演算法均以貝葉斯定理為基礎,故統稱為貝葉斯分類。
而樸素樸素貝葉斯分類是貝葉斯分類中最簡單,也是常見的一種分類方法
首先根據樣本中心定理,概率等於頻率,所以下文的P是可以統計出來的
樸素貝葉斯的核心便是貝葉斯公式:P(B|A)=P(A|B)P(B)/P(A) 即在A條件下,B發生的概率
換個角度:P(類別|特徵)=P(特徵|類別)P(類別)/P(特徵)
而我們最後要求解的就是P(類別|特徵)
舉一個生活中的例子:

最後一個公式中的所有概率都是可以統計出來的,所以P(B|A)可以計算!
那麼!我感覺我都寫偏題了,這明明是機器學習演算法概述嘛
那麼sklearn中怎麼實現呢?
import sklearn.naive_bayes as sk_bayes
model = sk_bayes.MultinomialNB(alpha=1.0,fit_prior=True,class_prior=None) #多項式分佈的樸素貝葉斯
model = sk_bayes.BernoulliNB(alpha=1.0,binarize=0.0,fit_prior=True,class_prior=None) #伯努利分佈的樸素貝葉斯
model = sk_bayes.GaussianNB()#高斯分佈的樸素貝葉斯
model.fit(X_train,y_train)
acc=model.score(X_test,y_test) #根據給定資料與標籤返回正確率的均值
print(n樸素貝葉斯(高斯分佈)模型評價:',acc)引數說明:
alpha:平滑引數
fit_prior:是否要學習類的先驗概率;false-使用統一的先驗概率
class_prior: 是否指定類的先驗概率;若指定則不能根據引數調整
binarize: 二值化的閾值,若為None,則假設輸入由二進位制向量組成
列印結果:
樸素貝葉斯(高斯分佈)模型評價: 0.92380952381決策樹
決策樹是解決分類問題
演算法描述請見我之前的帖子(寫的很詳細了):http://blackblog.tech/2018/01/29/決策樹——ID3演算法實現/
這裡我們直接上程式碼
import sklearn.tree as sk_tree
model = sk_tree.DecisionTreeClassifier(criterion='entropy',max_depth=None,min_samples_split=2,min_samples_leaf=1,max_features=None,max_leaf_nodes=None,min_impurity_decrease=0)
model.fit(X_train,y_train)
acc=model.score(X_test,y_test) #根據給定資料與標籤返回正確率的均值
print('決策樹模型評價:',acc)引數說明:
criterion :特徵選擇準則gini/entropy
max_depth:樹的最大深度,None-儘量下分
min_samples_split:分裂內部節點,所需要的最小樣本樹
min_samples_leaf:葉子節點所需要的最小樣本數
max_features: 尋找最優分割點時的最大特徵數
max_leaf_nodes:優先增長到最大葉子節點數
min_impurity_decrease:如果這種分離導致雜質的減少大於或等於這個值,則節點將被拆分。
列印結果:
決策樹模型評價: 0.942857142857SVM(支援向量機)
支援向量機是解決分類問題
目的:求解最大化間隔
支援向量機將向量對映到一個更高維的空間裡,在這個空間裡建立有一個最大間隔超平面。在分開資料的超平面的兩邊建有兩個互相平行的超平面。建立方向合適的分隔超平面使兩個與之平行的超平面間的距離最大化。其假定為,平行超平面間的距離或差距越大,分類器的總誤差越小。
SVM的關鍵在於核函式
一句話講懂核函式:低維無法線性劃分的問題放到高維就可以線性劃分,一般用高斯,因為效果絕對不會變差!
SVM演算法思路很清晰,但是實現起來很複雜,最近就在實現SVM,寫好了就發上來,在這裡就不贅述這麼多了,我們直接用skleran解決問題。
import sklearn.svm as sk_svm
model = sk_svm.SVC(C=1.0,kernel='rbf',gamma='auto')
model.fit(X_train,y_train)
acc=model.score(X_test,y_test) #根據給定資料與標籤返回正確率的均值
print('SVM模型評價:',acc)引數說明:
C:誤差項的懲罰引數C
kernel:核函式選擇 預設:rbf(高斯核函式),可選:‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’
gamma: 核相關係數。浮點數,If gamma is ‘auto’ then 1/n_features will be used instead.點將被拆分。
列印結果:
SVM模型評價: 0.961904761905神經網路
還在感慨因為不會tensorflow而無法使用神經網路?還在羨慕神經網路的驚人效果?不需要tf,不需要caffe,不需要pytorch!只要一句話,便可以實現多層神經網路!!!
在這裡還是簡單說一下M-P神經元的原理:
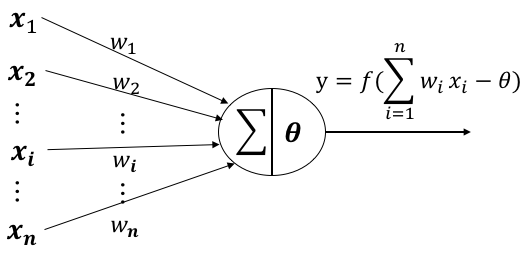
來自第個神經元的輸入
第個神經元的連線權重
閾值(threshold)或稱為偏置(bias)
為啟用函式,常用:sigmoid,relu,tanh等等
對於一個神經元來說,有i個輸入,每一個輸入都對應一個權重(w),神經元具有一個偏置(閾值),將所有的i*w求和後減去閾值得到一個值,這個值就是啟用函式的引數,啟用函式將根據這個引數來判定這個神經元是否被啟用。
本質上, M-P神經元=線性二分類器
那麼什麼是多層神經網路?
線性不可分:一個超平面沒法解決問題,就用兩個超平面來解決,什麼?還不行!那就再增加超平面直到解決問題為止。 ——多層神經網路
沒錯,多層神經元就是用來解決線性不可分問題的。
那麼,sklearn中如何實現呢?
import sklearn.neural_network as sk_nn
model = sk_nn.MLPClassifier(activation='tanh',solver='adam',alpha=0.0001,learning_rate='adaptive',learning_rate_init=0.001,max_iter=200)
model.fit(X_train,y_train)
acc=model.score(X_test,y_test) #根據給定資料與標籤返回正確率的均值
print('神經網路模型評價:',acc)引數說明:
hidden_layer_sizes: 元祖
activation:啟用函式 {‘identity’, ‘logistic’, ‘tanh’, ‘relu’}, 預設 ‘relu’
solver :優化演算法{‘lbfgs’, ‘sgd’, ‘adam’}
alpha:L2懲罰(正則化項)引數
learning_rate:學習率 {‘constant’, ‘invscaling’, ‘adaptive’}
learning_rate_init:初始學習率,預設0.001
max_iter:最大迭代次數 預設200
特別:
學習率中引數:
constant: 有‘learning_rate_init’給定的恆定學習率
incscaling:隨著時間t使用’power_t’的逆標度指數不斷降低學習率
adaptive:只要訓練損耗在下降,就保持學習率為’learning_rate_init’不變
優化演算法引數:
lbfgs:quasi-Newton方法的優化器
sgd:隨機梯度下降
adam: Kingma, Diederik, and Jimmy Ba提出的機遇隨機梯度的優化器
列印結果:(神經網路的確牛逼)
神經網路模型評價: 0.980952380952KNN(K-近鄰演算法)
KNN可以說是非常好用,也非常常用的分類演算法了,也是最簡單易懂的機器學習演算法,沒有之一。由於演算法先天優勢,KNN甚至不需要訓練就可以得到非常好的分類效果了。
在訓練集中資料和標籤已知的情況下,輸入測試資料,將測試資料的特徵與訓練集中對應的特徵進行相互比較,找到訓練集中與之最為相似的前K個數據,則該測試資料對應的類別就是K個數據中出現次數最多的那個分類。
其演算法的描述為:
1.計算測試資料與各個訓練資料之間的距離;
2.按照距離的遞增關係進行排序;
3.選取距離最小的K個點;
4.確定前K個點所在類別的出現頻率;
5.返回前K個點中出現頻率最高的類別作為測試資料的預測分類。
(感覺又說多了…… - -!)
其實這個演算法自己實現起來也就只有幾行程式碼,這裡我們還是使用sklearn來實現。
sklearn中的KNN可以做分類也可以做迴歸
import sklearn.neighbors as sk_neighbors
#KNN分類
model = sk_neighbors.KNeighborsClassifier(n_neighbors=5,n_jobs=1)
model.fit(X_train,y_train)
acc=model.score(X_test,y_test) #根據給定資料與標籤返回正確率的均值
print('KNN模型(分類)評價:',acc)
#KNN迴歸
model = sk_neighbors.KNeighborsRegressor(n_neighbors=5,n_jobs=1)
model.fit(X_train,y_train)
acc=model.score(X_test,y_test) #返回預測的確定係數R2
print('KNN模型(迴歸)評價:',acc)引數說明:
n_neighbors: 使用鄰居的數目
n_jobs:並行任務數
列印結果:
KNN模型(分類)評價: 0.942857142857
KNN模型(迴歸)評價: 0.926060606061交叉驗證
好的,終於說完了常用模型,感覺完全是一個演算法概述啊hhhhh
既然我們現在已經完成了資料的獲取,模型的建立,那麼最後一步便是驗證我們的模型
其實交叉驗證應該放在資料集的劃分那裡,但是他又與模型的驗證緊密相關,所以我就按照編寫程式碼的順序進行講解了。
首先,什麼是交叉驗證?
這裡完全引用西瓜書,因為我覺得書上寫的非常清楚!!!
交叉驗證法先將資料集D劃分為k個大小相似的互斥子集,每個子集Di都儘可能保持資料分佈的一致性,即從D中通過分層取樣得到。然後每次用k-1個子集的並集做為訓練集,餘下的子集做為測試集,這樣就可以獲得K組訓練/測試集,從而可以進行k次訓練和測試,最終返回的是這個k個測試結果的均值。k通常的取值是10,其他常用取值為2,5,20等。
這裡使用KNN做為訓練模型,採用十折交叉驗證。
model = sk_neighbors.KNeighborsClassifier(n_neighbors=5,n_jobs=1) #KNN分類
import sklearn.model_selection as sk_model_selection
accs=sk_model_selection.cross_val_score(model, iris_X, y=iris_y, scoring=None,cv=10, n_jobs=1)
print('交叉驗證結果:',accs)引數說明:
model:擬合數據的模型
cv : 子集個數 就是k
scoring: 打分引數 預設‘accuracy’、可選‘f1’、‘precision’、‘recall’ 、‘roc_auc’、’neg_log_loss’
列印結果:
交叉驗證結果:
[ 1. 0.93333333 1. 1. 0.86666667 0.93333333
0.93333333 1. 1. 1. ]模型的儲存和載入
模型的儲存和載入方便我們將訓練好的模型儲存在本地或傳送在網上,載入模型方便我們在不同的環境下進行測試。
使用pickle可以進行儲存與載入
也可以使用sklearn自帶的函式
import sklearn.externals as sk_externals
sk_externals.joblib.dump(model,'model.pickle') #儲存
model = sk_externals.joblib.load('model.pickle') #載入小結
兩篇帖子基本完成了對於sklearn的基礎講解,看似內容雖多,但是使用起來其實非常簡單。不小心寫成一個演算法概述,也沒什麼太大的問題,相信我不寫,大家也會去百度這些演算法的含義,我就當這是為大家省時間了吧哈哈哈。
sklearn是一個非常好用的機器學習工具包,掌握好它會在機器學習的道路上祝我們一臂之力的!
與君共勉!
