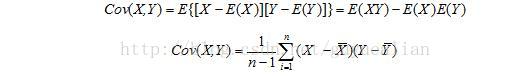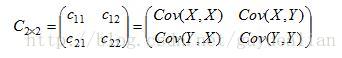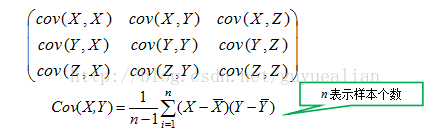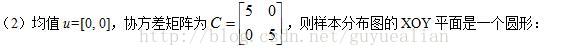協方差矩陣和散佈矩陣的意義

      在機器學習模式識別中，經常需要應用到協方差矩陣C和散佈矩陣S。如在PCA主成分分析中，需要計算樣本的散度矩陣，有的論文是計算協方差矩陣。實質上二者意義差不多，散佈矩陣（散度矩陣）前乘以係數1/(n-1)就可以得到協方差矩陣了。

   在模式識別的教程中，散佈矩陣也稱為散度矩陣，有的也稱為類內離散度矩陣或者類內離差陣，用一個等式關係可表示為：

關係：散度矩陣=類內離散度矩陣=類內離差陣=協方差矩陣×（n-1）

    樣本的協方差矩陣乘以n-1倍即為散佈矩陣，n

一、協方差矩陣的基礎

   對於二維隨機變數（X,Y）之間的相互關係的數字特徵，我們用協方差來描述，記為Cov(X,Y)：

那麼二維隨機變數(X,Y)的協方差矩陣，為：

對於三維隨機變數X=（X₁, X_{2, X3}）的協方差矩陣可表示為：

        對於n維X=（X₁, X₂....X _n）協方差矩陣：

說明：

     （1）協方差矩陣是一個對稱矩陣，且是半正定矩陣，主對角線是各個隨機變數的方差（各個維度上的方差）。

   （2）標準差和方差一般是用來描述一維資料的；對於多維情況，而協方差是用於描述任意兩維資料之間的關係，一般用協方差矩陣來表示。

   （3）協方差計算過程可簡述為：先求各個分量的均值E(Xi)和E(Xj)，然後每個分量減去各自的均值得到兩條向量，在進行內積運算，然後求內積後的總和，最後把總和除以n-1。

例子：設有8個樣本資料，每個樣本有2個特徵：(1,2);(3 3);(3 5);(5 4);(5 6);(6 5);(8 7);(9 8)，那麼可以看作二維的隨機變數（X,Y），即

   X =[1 3 3 5 5 6 8 9]

   Y =[2 3 5 4 6 5 7 8]

   Matlab中可以使用cov(X, Y)函式計算樣本的協方差矩陣，其中X,Y都是特徵向量。當然若用

clear all
clc
X=[1,2;3 3;3 5;5 4;5 6;6 5;8 7;9 8]%樣本矩陣：8個樣本，每個樣本2個特徵
covX= cov(X)%使用cov函式求協方差矩陣

covX =

    7.1429    4.8571
    4.8571    4.0000

clear all
clc
X=[1,2;3 3;3 5;5 4;5 6;6 5;8 7;9 8] %樣本矩陣：8個樣本，每個樣本2個特徵
covX= cov(X)                                %使用cov函式求協方差矩陣
%% 按定義求協方差矩陣：（1）使用分量的方法，先求協方差，再組合成協方差矩陣
meanX=mean(X)        %樣本均值
varX=var(X)               %樣本方差
[Row Col]=size(X);
dimNum=Row;          %s樣本個數size(X,1)=8
dim1=X(:,1);              %特徵分量1
dim2=X(:,2);              %而在分量2
c11=sum( (dim1-mean(dim1)) .* (dim1-mean(dim1)) ) / ( dimNum-1 );
c21=sum( (dim2-mean(dim2)) .* (dim1-mean(dim1)) ) / ( dimNum-1 ); 
c12=sum( (dim1-mean(dim1)) .* (dim2-mean(dim2)) ) / ( dimNum-1 ); 
c22=sum( (dim2-mean(dim2)) .* (dim2-mean(dim2)) ) / ( dimNum-1 );
C22=[c11,c12;c21,c22]%協方差矩陣

%% 或者（2）直接求協方差矩陣：
tempX= repmat(meanX,Row,1);  
C22=(X-tempX)'*(X-tempX)/(dimNum-1)

covX =

    7.1429    4.8571
    4.8571    4.0000

meanX =

     5     5

varX =

    7.1429    4.0000

C22 =

    7.1429    4.8571
    4.8571    4.0000

C22 =

    7.1429    4.8571
    4.8571    4.0000

二、協方差矩陣的意義

為了更好理解協方差矩陣的幾何意義，下面以二維正態分佈圖為例（假設樣本服從二維正態分佈）：

clear all;clc
mu=[0,0];         % 均值向量
C=[5 0;0 1]       %樣本的協方差矩陣
[V,D] =eigs(C)    %求協方差矩陣的特徵值D和特徵向量V
 %% 繪製二維正態分佈圖
[X,Y]=meshgrid(-10:0.3:10,-10:0.3:10);%在XOY面上，產生網格資料
p=mvnpdf([X(:) Y(:)],mu,C);%求取聯合概率密度，相當於Z軸
p=reshape(p,size(X));%將Z值對應到相應的座標上
figure
set(gcf,'Position',get(gcf,'Position').*[1 1 1.3 1])
subplot(2,3,[1 2 4 5])
surf(X,Y,p),axis tight,title('二維正態分佈圖')
subplot(2,3,3)
surf(X,Y,p),view(2),axis tight,title('在XOY面上的投影')
subplot(2,3,6)
surf(X,Y,p),view([0 0]),axis tight,title('在XOZ面上的投影');

V =
     1     0
     0     1

D =
     5     0
     0     1

說明：

   1)均值[0,0]代表正態分佈的中心點，方差代表其分佈的形狀。

   2)協方差矩陣C的最大特徵值D對應的特徵向量V指向樣本分佈的主軸方向。例如，最大特徵值D1=5對應的特徵向量V1=[1 0]^T即為樣本分佈的主軸方向（一般認為是資料的傳播方向）。次大特徵值D2=1對應的特徵向量V2=[0 1]^T,即為樣本分佈的短軸方向。

協方差矩陣C的特徵值D和特徵向量V分別為：

V =
     0     1
     1     0

D =

     5     0
     0     5

 說明：

   1)由於協方差矩陣C具有兩個相同的特徵值D1=D2=5,因此樣本在V1和V2特徵向量方向的分佈是等程度的，故樣本分佈是一樣圓形。

   2)特徵值D1和D2的比值越大，資料分佈形狀就越扁；當比值等於1時，此時樣本資料分佈為圓形。

協方差矩陣C的特徵值D和特徵向量V分別為：

V =
    0.7071   -0.7071
    0.7071    0.7071

D =
     6     0
     0     4

 說明：

   1)特徵值的比值D1/D2=6/4=1.5>1，因此樣本資料分佈形狀是扁形，資料傳播方向（樣本的主軸方向）為V1=[0.7071 0.7071]^T

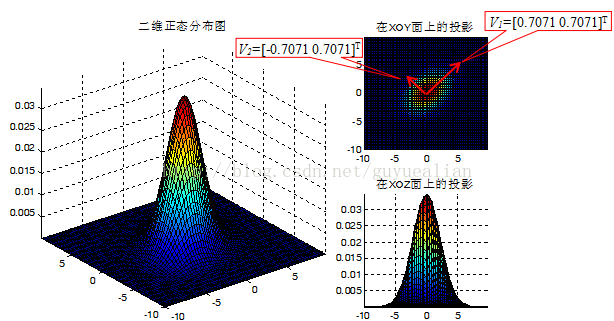
綜合上述，可知： 

(1)樣本均值決定樣本分佈中心點的位置。

(2)協方差矩陣決定樣本分佈的扁圓程度。

   是扁還是圓，由協方差矩陣的特徵值決定：當特徵值D1和D2的比值為1時（D1/D2=1），則樣本分佈形狀為圓形。當特徵值的比值不為1時，樣本分佈為扁形；

   偏向方向（資料傳播方向）由特徵向量決定。最大特徵值對應的特徵向量，總是指向資料最大方差的方向（橢圓形的主軸方向）。次大特徵向量總是正交於最大特徵向量（橢圓形的短軸方向）。

三、協方差矩陣的應用

    協方差矩陣（散佈矩陣）在模式識別中應用廣泛，最典型的應用是PCA主成分分析了，PCA主要用於降維，其意義就是將樣本資料從高維空間投影到低維空間中，並儘可能的在低維空間中表示原始資料。這就需要找到一組最合適的投影方向，使得樣本資料往低維投影后，能儘可能表徵原始的資料。此時就需要樣本的協方差矩陣。PCA演算法就是求出這堆樣本資料的協方差矩陣的特徵值和特徵向量，而協方差矩陣的特徵向量的方向就是PCA需要投影的方向。

    關於PCA的原理和分析，請見鄙人的部落格：

    《PCA主成分分析原理分析和Matlab實現方法》：http://blog.csdn.net/guyuealian/article/details/68487833