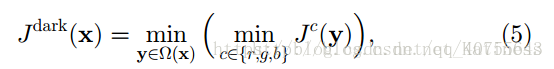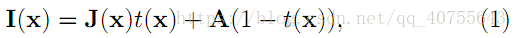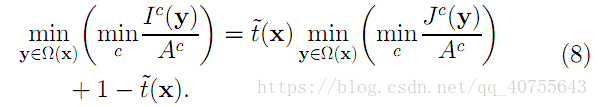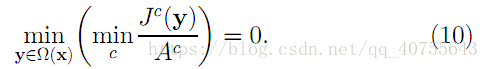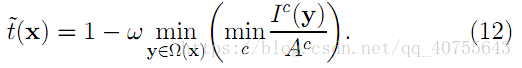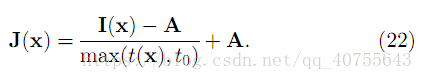He 提出暗通道去霧方法進行了詳細的描述，該方法以大氣散射模型為基礎，利用暗通道先驗原理求出全球大氣光成分A和透射率t。先使用了軟摳圖對透射率圖進行優化，但是運算時間過長。後來使用引導濾波精細化透射率圖，縮短了一部分運算時間。

暗通道先驗：

在絕大多數非天空的區域性區域裡，某一些畫素總會有至少一個RGB顏色通道具有很低的值。換言之，該區域光強度的最小值是個很小的數，值接近於0。

實際生活中造成暗原色中低通道值主要有三個因素：

a)汽車、建築物和城市中玻璃窗戶的陰影，或者是樹葉、樹與岩石等自然景觀的投影；

b)色彩鮮豔的物體或表面，在RGB的三個通道中有些通道的值很低（比如綠色的草地／樹／植物，紅色或黃色的花朵／葉子，或者藍色的水面）；

c)顏色較暗的物體或者表面，例如灰暗色的樹幹和石頭。總之，自然景物中到處都是陰影或者彩色，這些景物的影象的暗原色總是很灰暗的。

我們給暗通道一個數學定義，對於任意的輸入影象J，其暗通道可以用下式表達：

c表示影象R,G,B中的每個通道。

Jc表示彩色影象的某一通道 。

Ω(x)表示以畫素X為中心的一個視窗。

 式（5）的意義用程式碼表達也很簡單，求解過程如下：

（1）求出每個畫素RGB分量中的最小值，存入一副和原始影象大小相同的灰度圖中

（2）對這幅灰度圖以15x15的視窗進行最小值濾波，即以每個視窗的最小值代替這個畫素點的最小值。濾波的半徑由視窗大小決           定（論文采用7），一般有WindowSize = 2 * Radius + 1; 

def darkChannel(src, r=15):
    
    temp = np.min(src,2)
    
    s = cv2.getStructuringElement(cv2.MORPH_ELLIPSE, (r,r))

    dst = cv2.erode(temp, s)
    
    return dst

舉個栗子：

由上述幾幅影象，可以明顯的看到暗通道先驗理論的普遍性。在作者的論文中，對5000多副無霧影象手動裁剪掉天空區域，重調整圖片大小，使得圖片長寬不大於500，Ω(x)的大小選取15*15，發現75%的暗通道的畫素值都為0，90%的暗通道的畫素值都低於25，很好驗證暗通道理論的普適性，因此，我們可以認為其實一條定理。

大氣散射模型（求解A與t(x)）：

在計算機視覺和計算機圖形中，下述方程所描述的霧圖形成模型被廣泛使用：

I(X)就是我們現在已經有的影象（待去霧的影象）。

J(x)是我們要恢復的無霧的影象。

A是全球大氣光成分， t(x)為透射率。

將式（1）稍作處理，變形為下式（C表示R/G/B三個通道的意思）：

首先假設在每一個視窗內透射率t(x)為常數，也就是假設在同一視窗的上的透射率是相同的，定義他為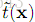，且A值已經給定，然後對式（7）兩邊求兩次最小值運算得到下式：

上式中，J是待求的無霧的影象，根據前述的暗原色先驗理論有：

可推匯出：

把式（10）帶入式（8）中，得到：

這裡使用guideFilter引導濾波，優化已經求得的通道圖片，所以上式變為t=1-V/A，這裡V為透射率圖。

引導圖應該與原圖儘可能相似，取np.min(src,2)

也就是：V = guideFilter(np.min(m,2) , dc, r, eps)，這裡應該在[0,1]範圍內進行，也就是引導圖和預估的投射圖都必須從[0,255]->[0,1]進行計算。導向濾波的r值應當不小於進行最小值濾波半徑r的4倍。

即使是晴天白雲，空氣中也存在著一些顆粒，因此，看遠處的物體還是能感覺到霧的影響，另外，霧的存在讓人類感到景深的存在，因此，有必要在去霧的時候保留一定程度的霧，這可以通過在式（11）中引入一個在[0,1] 之間的因子，則式（11）修正為：

注：文中所有的測試結果依賴於：  ω=0.95

上述推論中都是假設全球達氣光A值時已知的，在實際中，我們可以藉助於暗通道圖來從有霧影象中獲取該值。具體步驟如下：

（1） 從暗通道圖中按照亮度的大小取前0.1%的畫素。（經過導向濾波這應為投射率圖）

（2）在這些位置中，在原始有霧影象I中尋找對應的具有最高亮度的點的值，作為A值。

使用累計灰度直方圖來實現求A值

bins = 256  
hist = np.histogram(V, bins)                  #灰度直方圖

這裡V是待統計資料陣列，bins為等分數。返回值有兩個：

hist[0]：hist:array，返回陣列V中的資料在每個等分割槽間的個數。

hist[1]：bin_degs，長度為len(hist)+1，為分組的邊界。(bin_degs[0], bin_edgs[1])=hist[0]

normHist = hist[0]/float(V.size)              #歸一化灰度直方圖

概率直方圖,灰度值k的畫素點個數佔的圖比例

accumulativeHist = np.cumsum(normHist)    #累計直方圖

代表影象組成成分在灰度級的累計概率分佈情況，每一個概率值代表小於等於此灰度值的概率。

for k in range(bins-1, 0, -1):
        
        if accumulativeHist[k]<=0.999:             #取前0.1%的畫素，並獲得該位置k
            break 
        
A  = np.mean(m,2)[V>=hist[1][k]].max()        #在原始有霧的影象I中尋找對應的具有最高亮度的點的值

這裡返回的k值就是邊界值k。

到這一步，我們就可以進行無霧影象的恢復了。由式（1）可知：  J = ( I - A)/t + A  

現在I,A,t都已經求得了，因此，完全可以進行J的計算。

當投射圖t 的值很小時，會導致J的值偏大，從而使淂影象整體向白場過度，因此一般可設定一閾值T0，當t值小於T0時，令t=T0，本文中所有效果圖均以T0=0.1為標準計算。

因此，最終的恢復公式如下：

Python程式碼實現：

# -*- coding: utf-8 -*-
"""
Created on Thu Nov 15 16:49:29 2018

@author: x
"""
import cv2  
import numpy as np 
import os.path
import glob

# time start
t1 = cv2.getTickCount() 
   
def darkChannel(src, r=15):
    temp = np.min(src,2)
    s = cv2.getStructuringElement(cv2.MORPH_ELLIPSE, (r,r))
    dst = cv2.erode(temp, s) 
    return dst

def guideFilter(I, p, r, eps):
    #I的均值平滑
    mean_I = cv2.blur(I, (r, r))
    #p的均值平滑
    mean_p = cv2.blur(p, (r, r))
    #I*I和I*p的均值平滑
    mean_II = cv2.blur(I*I, (r, r))
    mean_Ip = cv2.blur(I*p, (r, r))
    #方差
    var_I = mean_II - mean_I * mean_I #方差公式
    #協方差
    cov_Ip = mean_Ip - mean_I * mean_p
    a = cov_Ip / (var_I + eps)
    b = mean_p - a*mean_I
    #對a、b進行均值平滑
    mean_a = cv2.blur(a, (r, r))
    mean_b = cv2.blur(b, (r, r))
    q = mean_a*I + mean_b
    return q

def getParameter(m, r, eps, w, t0):  #輸入rgb影象，值範圍[0,1]  
    dc = darkChannel(m)                           #得到暗通道影象
    V = guideFilter(np.min(m,2) , dc, r, eps)     #使用引導濾波優化，獲得透射率圖V
    bins = 256  
    hist = np.histogram(V, bins)                  #灰度直方圖
    normHist = hist[0]/float(V.size)              #歸一化灰度直方圖,即概率直方圖,灰度值k的畫素點個數佔的圖比例
    accumulativeHist = np.cumsum(normHist)         #累計直方圖，代表影象組成成分在灰度級的累計概率分佈情況，
                                                   #每一個概率值代表小於等於此灰度值的概率
    for k in range(bins-1, 0, -1):
        
        if accumulativeHist[k]<=0.999:             #取前0.1%的畫素，並獲得該位置k
            break 
        
    A  = np.mean(m,2)[V>=hist[1][k]].max()        #在原始有霧的影象I中尋找對應的具有最高亮度的點的值
    #if A > 220/255.0:                               #全球大氣光成分最大值取220
     #   A = 220/255.0      
    V = V*w                                       #修正因子
    t = 1 - V/A
    t = np.maximum(t, t0)   
    return t,A
       
def hazeRemoval(m, r=75, eps=0.001, w=0.95, t0=0.10, bGamma=False):  
    
    J = np.zeros(m.shape)  
    t, A = getParameter(m, r, eps, w, t0)               #得到遮罩影象和大氣光照      
    for k in range(3):  
        J[:,:,k] = (m[:,:,k]-A)/t + A                  #三通道去霧還原圖片
        
    J =  np.clip(J, 0, 1)                             #將值限制在[0,1]之間,因為圖片已經歸一化了    
    if bGamma:  
        J = J**(np.log(0.5)/np.log(J.mean()))       #gamma校正,預設不進行該操作  
    return J
        
def batchProcess(jpgfile,outdir):
    
    img = cv2.imread(jpgfile, cv2.IMREAD_ANYCOLOR)    
    try:
        new_img= hazeRemoval(img/255.0)*255 
        cv2.imwrite(os.path.join(outdir,os.path.basename(jpgfile)), new_img)
        
    except Exception as e:
        print(e)
        
if __name__ == '__main__':
    for jpgfile in glob.glob(r'C:\Users\x\Desktop\kk\*.jpg'):
        batchProcess(jpgfile,r'C:\Users\x\Desktop\t')
    
# time end
t2 = cv2.getTickCount()
    
t = (t2-t1)/cv2.getTickFrequency()
print ("耗時為：")
print (t)

實驗結果對比: