如果你對機器學習感興趣，請參看一下連結：
機器學習：神經網路導論

對二叉樹節點的遍歷一般來說有中序，後序，和前序三種遍歷方法，如果二叉樹的高用h來表示，那三種遍歷方法所需要的空間複雜度為O(h). 例如對於中序遍歷來說，如果我們使用遞迴來實現的話，程式碼如下：

void inorderTraval(TreeNode root) {
    if (root == null) {
        return;
    }

    inorderTraval(root.left);
    System.out.print(root.value + " ");
    inorderTraval(root.right);
}
 

上面的實現中，有函式的遞迴呼叫，遞迴的深度等於二叉樹的高度，也就是說遞迴導致的呼叫堆疊的高度等於二叉樹的高度，這樣的話，程式雖然沒有顯示的通過new 來分配記憶體，但實際上消耗的記憶體大小也是 O(h). 如果二叉樹的高度很大，例如搜尋引擎把幾十億張網頁按照權重來組成二叉樹的話，那麼二叉樹的高度也要幾十萬作用，因此按照傳統的中序遍歷，需要消耗大量的記憶體。

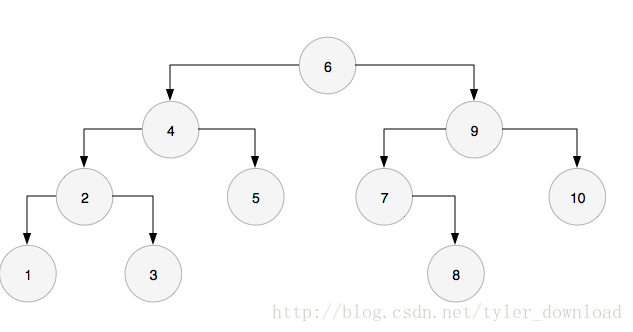
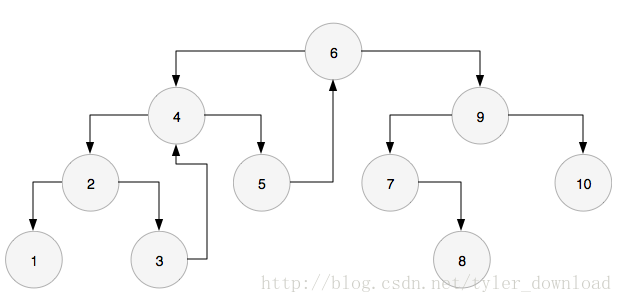
本節要講的Morris遍歷法，能以O(1)的空間複雜度實現二叉樹的中序遍歷。例如給定下面二叉樹：

採用中序遍歷的話，二叉樹節點的訪問情況如下：

1，2，3，4，5，6，7，8，9，10

給定某個節點，在中序遍歷中，直接排在它前面的節點，我們稱之為該節點的前序節點，例如節點5的前序節點就是4，同理，節點10的前序節點就是9.

在二叉樹中如何查詢一個節點的前序節點呢？如果該節點有左孩子，那麼從左孩子開始，沿著右孩子指標一直想有走到底，得到的節點就是它的前序節點，例如節點6的左孩子是4，沿著節點4的右指標走到底，那就是節點5，節點9的左孩子是7，沿著它的右指標走到底對應的節點就是8.

如果左孩子的右節點指標是空，那麼左孩子就是當前節點的前序節點。

如果當前節點沒有左孩子，並且它是其父節點的右孩子，那麼它的前序節點就是它的父節點，例如8的前序節點是7，10的前序節點是9.

如果當前節點沒有左孩子，並且它是父節點的左孩子，那麼它沒有前序節點，並且它自己就是首節點，例如節點1.

值得注意的是，前序節點的右指標一定是空的。

Morris遍歷演算法的步驟如下：

1， 根據當前節點，找到其前序節點，如果前序節點的右孩子是空，那麼把前序節點的右孩子指向當前節點，然後進入當前節點的左孩子。

2， 如果當前節點的左孩子為空，列印當前節點，然後進入右孩子。

3，如果當前節點的前序節點其右孩子指向了它本身，那麼把前序節點的右孩子設定為空，列印當前節點，然後進入右孩子。

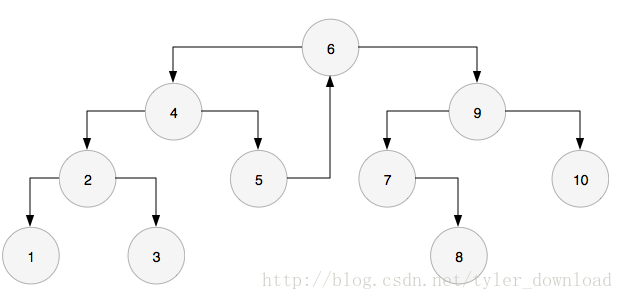
我們以上面的例子走一遍。首先訪問的是根節點6，得到它的前序節點是5，此時節點5的右孩子是空，所以把節點5的右指標指向節點6：

進入左孩子，也就到了節點4，此時節點3的前序節點3，右孩子指標是空，於是節點3的右孩子指標指向節點4，然後進入左孩子，也就是節點2

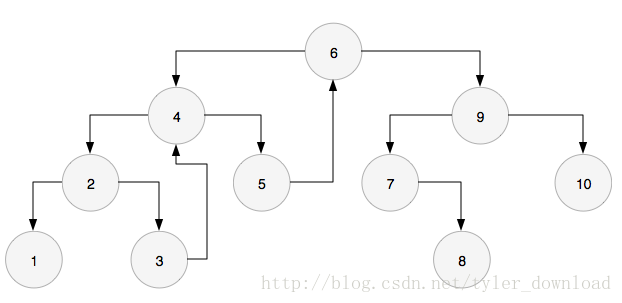
此時節點2的左孩子1沒有右孩子，因此1就是2的前序節點，並且節點1的右孩子指標為空，於是把1的右孩子指標指向節點2，然後從節點2進入節點1：

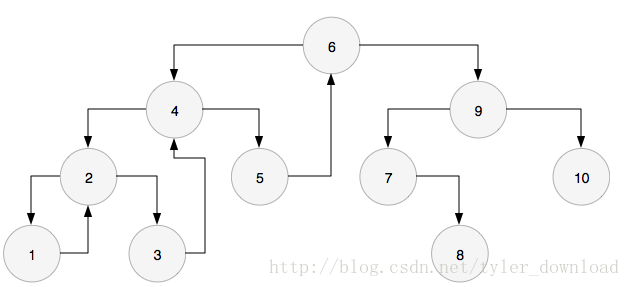
此時節點1沒有左孩子，因此列印它自己的值，然後進入右孩子，於是回到節點2.根據演算法步驟，節點2再次找到它的前序節點1，發現前序節點1的右指標已經指向它自己了，所以列印它自己的值，同時把前序節點的右孩子指標設定為空，同時進入右孩子，也就是節點3.於是圖形變為：

此時節點3沒有左孩子，因此列印它自己的值，然後進入它的右孩子，也就是節點4. 到了節點4後，根據演算法步驟，節點4先獲得它的前序節點，也就是節點3，發現節點3的右孩子節點已經指向自己了，所以列印它自己的值，也就是4，然後把前序節點的右指標設定為空，於是圖形變成：

接著從節點4進入右孩子，也就是節點5，此時節點5沒有左孩子，所以直接列印它本身的值，然後進入右孩子，也就是節點6，根據演算法步驟，節點6獲得它的前序節點5，發現前序節點的右指標已經指向了自己，於是就列印自己的值，把前序節點的右指標設定為空，然後進入右孩子。

接下來的流程跟上面一樣，就不再重複了。我們看看具體的實現程式碼：

public class MorrisTraval {
    private TreeNode root = null;
    public MorrisTraval(TreeNode r) {
        this.root = r;
    }

    public void travel() {
        TreeNode n = this.root;

        while (n != null) {
            if (n.left == null) {
                System.out.print(n.vaule + " ");
                n = n.right;
            } else {
                TreeNode pre = getPredecessor(n);

                if (pre.right == null) {
                    pre.right = n;
                    n = n.left;
                }else if (pre.right == n) {
                    pre.right = null;
                    System.out.print(n.vaule + " ");
                    n = n.right;
                }

            }
        }
    }

    private TreeNode getPredecessor(TreeNode n) {
        TreeNode pre = n;
        if (n.left != null) {
            pre = pre.left;
            while (pre.right != null && pre.right != n) {
                pre = pre.right;
            }
        }

        return pre;
    }

}

getPredecessor 作用是獲得給定節點的前序節點，travel 介面做的就是前面描述的演算法步驟，在while迴圈中，進入一個節點時，先判斷節點是否有左孩子，沒有的話就把節點值打印出來，有的話，先獲得前序節點，然後判斷前序節點的右孩子指標是否指向自己，是的話把自己的值打印出來，進入右孩子，前序孩子的右孩子指標是空的話，就把右孩子指標指向自己，然後進入左孩子。

Morris遍歷，由於要把字首節點的右指標指向自己，所以暫時會改變二叉樹的結構，但在從字首節點返回到自身時，演算法會把字首節點的右指標重新設定為空，所以二叉樹在結構改變後，又會更改回來。

在遍歷過程中，每個節點最多會被訪問兩次，一次是從父節點到當前節點，第二次是從字首節點的右孩子指標返回當前節點，所以Morris遍歷演算法的複雜度是O(n)。在遍歷過程中，沒有申請新記憶體，因此演算法的空間複雜度是O(1).

更多技術資訊，包括作業系統，編譯器，面試演算法，機器學習，人工智慧，請關照我的公眾號：