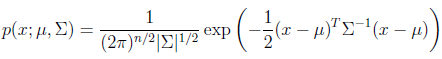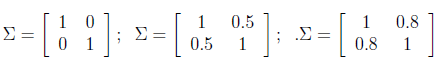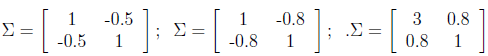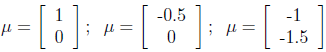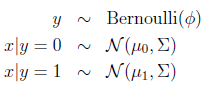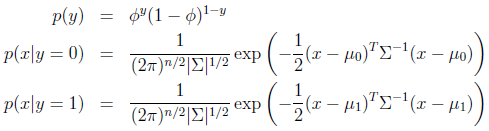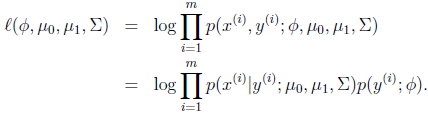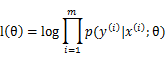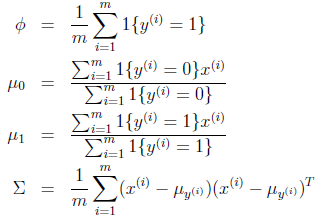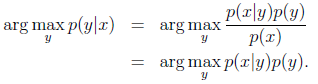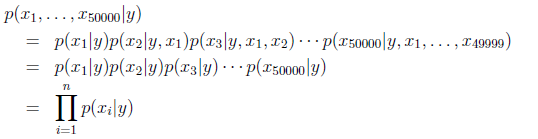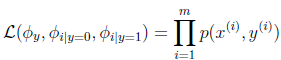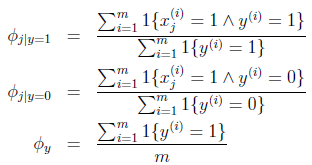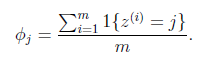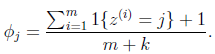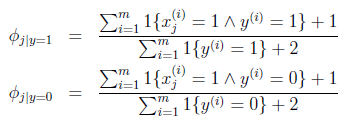生成學習演算法

本次課程大綱：

1、 生成學習演算法

2、 高斯判別分析（GDA，Gaussian Discriminant Analysis）

-          高斯分佈（簡要）

-          對比生成學習演算法&判別學習演算法（簡要）

3、 樸素貝葉斯

4、 Laplace平滑

複習：

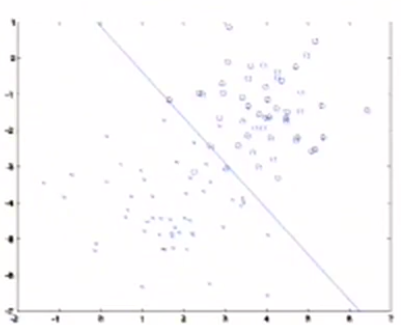
分類演算法：給出一個訓練集，若使用logistic迴歸演算法，其工作方式是觀察這組資料，嘗試找到一條直線將圖中不同的類分開，如下圖。

之前講的都是判別學習演算法，本課介紹一種不同的演算法：生成學習演算法。

1、 生成學習演算法

例：對惡性腫瘤和良性腫瘤的分類

除了尋找一個將兩類資料區分的直線外，還可以用如下方法：

1)       遍歷訓練集，找到所有惡性腫瘤樣本，直接對惡性腫瘤的特徵建模；同理，對良性腫瘤建模。

2)       對一個新的樣本分類時，即有一個新的病人時，要判斷其是惡性還是良性，用該樣本分別匹配惡性腫瘤模型和良性腫瘤模型，看哪個模型匹配的更好，預測屬於惡性還是良性。

這種方法就是生成學習演算法。

兩種學習演算法的定義：

1)       判別學習演算法：

-          直接學習p(y|x)，即給定輸入特徵，輸出所屬的類

-          或學習得到一個假設hθ(x)，直接輸出0或1

2)       生成學習演算法：

-          對p(x|y)進行建模，p(x|y)

-          p(x|y)中的x表示一個生成模型對樣本特徵建立概率模型，y表示在給定樣本所屬類的條件下

例：在上例中，假定一個腫瘤情況y為惡性和良性，生成模型會對該條件下的腫瘤症狀x的概率分佈進行建模

-          對p(x|y)和p(y)建模後，根據貝葉斯公式p(y|x) = p(xy)/p(x) = p(x|y)p(y)/p(x)，可以計算：p(y=1|x) = p(x|y=1)p(y=1)/p(x)，其中，p(x) = p(x|y=0)p(y=0) + p(x|y=1)p(y=1)

2、

GDA是一種生成學習演算法。

GDA的假設條件：

1)       假設輸入特徵x∈Rⁿ，並且是連續值。

2)       假設p(x|y)滿足高斯分佈

*高斯分佈基礎知識：

設隨機變數z滿足多元高斯分佈，z~N(μ,∑)，均值向量為μ，協方差矩陣為∑。

其概率密度函式為：

多元高斯分佈為一元高斯分佈的推廣，也是鐘形曲線，z是一個高維向量。

多元高斯分佈注意兩個引數即可：

-          均值向量μ

-          協方差矩陣∑= E[(Z-E[Z])(Z-E[Z])^T]=E[(x-μ)(x-μ)^T]

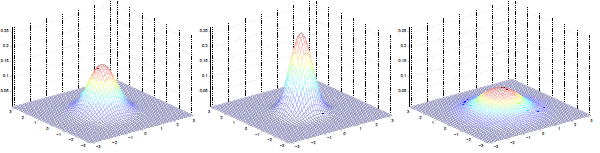
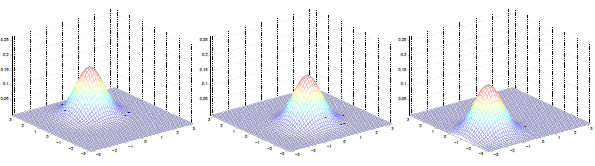
多元高斯分佈圖：

左圖：μ=0，∑=I（單位矩陣）

中圖：μ=0，∑=0.6I，圖形變陡峭

右圖：μ=0，∑=2I，圖形變扁平

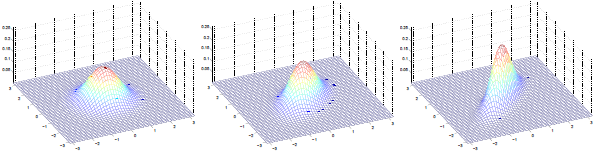
三圖中μ=0，∑如下：

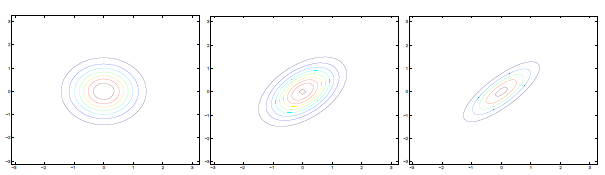
可見增加矩陣對角元素的值，即變數間增加相關性，高斯曲面會沿z1=z2（兩個水平軸）方向趨於扁平。其水平面投影圖如下：

即增加∑對角線的元素，圖形會沿45°角，偏轉成一個橢圓形狀。

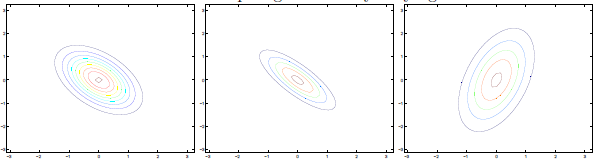
若∑對角線元素為負，圖形如下：

∑分別為：

不同μ的圖形如下：

μ分別為：

μ決定分佈曲線中心的位置。

GDA擬合：

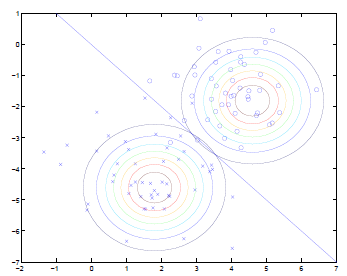
給出訓練樣本如下圖所示：

-          觀察正樣本（圖中的x），擬合正樣本的高斯分佈，如圖中左下方的圓，表示p(x|y=1)

-          觀察負樣本（圖中的圈），擬合負樣本的高斯分佈，如圖中右上方的圓，表示p(x|y=0)

-          通過這兩個高斯分佈的密度函式，定義出兩個類別的分隔器，即圖中的直線

-          這條分隔器直線比之前的logistic擬合的直線要複雜

GDA模型：

寫出其概率分佈：

引數包括φ，μ0，μ1，∑，對數似然性為：

由於第一個等式為xy的聯合概率，將這個模型命名為聯合似然性（Joint likelihood）。

*對比logistic迴歸中的對數似然性：

由於計算的是y在x條件下的概率，將此模型命名為條件似然性（conditional likelihood）

通過對上面對數似然性求極大似然估計，引數的結果為：

φ：訓練樣本中標籤為1的樣本所佔的比例

μ0：分母為標籤為0的樣本數，分子是對標籤為0的樣本的x(i)求和，結合起來就是對對標籤為0的樣本的x(i)求均值，與高斯分佈引數μ為均值的意義相符

μ1：與μ0同理，標籤改為1

GDA預測：

預測結果應該是給定x的情況下最可能的y，等式左邊的運算子argmax表示計算p(y|x)最大時的y值，預測公式如下：

因為p(x)獨立於y，所以可以忽略p(x)。

*如果p(y)為均勻分佈，即每種型別的概率都相同，那麼也可以忽略p(y)，要求的就是使p(x|y)最大的那個y。不過這種情況並不常見。

GDA和logistic迴歸的聯絡：

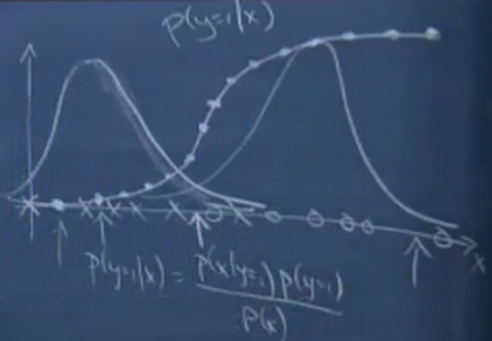
例：假設有一個一維訓練集，包含一些正樣本和負樣本，如下圖x軸的叉和圈，設叉為0，圈為1，用GDA對兩類樣本分別擬合高斯概率密度函式p(x|y=0)和p(x|y=1)，如下圖的兩個鐘形曲線。沿x軸遍歷樣本，在x軸上方畫出其相應的p(y=1|x)。

如選x軸靠左的點，那麼它屬於1的概率幾乎為0，p(y=1|x)=0，兩條鐘形曲線交點處，屬於0或1的概率相同，p(y=1|x)=0.5，x軸靠右的點，輸出1的概率幾乎為1，p(y=1|x)=1。最終發現，得到的曲線和sigmoid函式曲線很相似。

簡單來講，就是當使用GDA模型時，p(x|y)屬於高斯分佈，計算p(y|x)時，幾乎能得到和logistic迴歸中使用的sigmoid函式一樣的函式。但實際上還是存在本質區別的。

使用生成學習演算法的優缺點：

給出兩個推論：

推論1：

x|y 服從高斯分佈  =>  p(y=1|x)是logistic函式

該推論在反方向不成立。

推論2：

x|y=1 ~ Poisson(λ1)，x|y=0 ~ Poisson(λ0)  =>  p(y=1|x)是logistic函式

x|y=1 ~ Poisson(λ1)表示x|y=1服從引數為λ1泊松分佈

推論3：

x|y=1 ~ ExpFamily(η1)，x|y=0 ~ ExpFamily (η0)  =>  p(y=1|x)是logistic函式

推論2的推廣，即x|y的分佈屬於指數分佈族，均可推出結論。顯示了logistic迴歸在建模假設選擇方面的魯棒性。

優點：

推論1反方向不成立，因為x|y服從高斯分佈這個假設更強，GDA模型做出了一個更強的假設，所以，若x|y服從或近似服從高斯分佈，那麼GDA會比logistic迴歸更好，因為它利用了更多關於資料的資訊，即演算法知道資料服從高斯分佈。

缺點：

如果不確定x|y的分佈情況，那麼判別演算法logistic迴歸效能更好。例如，預先假設資料服從高斯分佈，但是實際上資料服從泊松分佈，根據推論2，logistic迴歸仍能獲得不錯的效果。

生成學習演算法比判決學習演算法需要更少的資料。如GDA的假設較強，所以用較少的資料能擬合出不錯的模型。而logistic迴歸的假設較弱，對模型的假設更為健壯，擬合數據需要更多的樣本。

3、 樸素貝葉斯

另一種生成學習演算法。

例：垃圾郵件分類

實現一個垃圾郵件分類器，以郵件輸入流作為輸入，確定郵件是否為垃圾郵件。輸出y為{0,1}，1為垃圾郵件，0為非垃圾郵件。

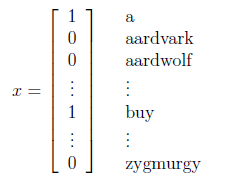
首先，要將郵件文字表示為一個輸入向量x，設已知一個含有n個詞的字典，那麼向量x的第i個元素{0,1}表示字典中的第i個詞是否出現在郵件中，x示例如下：

要對p(x|y)建模，x是一個n維的{0,1}向量，假設n=50000，那麼x有2^50000種可能的值，一種方法是用多項式分佈進行建模（伯努利分佈對01建模，多項式分佈對k個結果建模），這樣就需要2^50000-1個引數，可見引數過多，下面介紹樸素貝葉斯的方法。

假設xi在給定y的時候是條件獨立的，則x在給定y下的概率可簡化為：

這個假設直觀理解為，已知一封郵件是不是垃圾郵件(y)，以及一些詞是否出現在郵件中，這些並不會幫助你預測其他的詞是否出現在郵件中。雖然這個假設不是完全正確的，但是樸素貝葉斯依然應用於對郵件進行分類，對網頁進行分類等用途。

*對於樸素貝葉斯，我的理解為：通過指定一些垃圾郵件的關鍵詞來計算某個郵件是垃圾郵件的概率。具體講，就是給定字典後，給出每個詞的p(xi|y=1)，即這個詞xi在垃圾郵件中出現的概率，然後對於一個郵件，將郵件所有詞的p(xi|y)的相乘，就是郵件為垃圾郵件的概率。再簡化一些，規定p(xi|y=1)={0,1}，即劃定一些關鍵詞，這些關鍵詞在郵件中出現的概率就是這封郵件為垃圾郵件的概率。

模型引數包括：

Φi|y=1 = p(xi=1|y=1)

Φi|y=0 = p(xi=1|y=0)

Φy = p(y=1)

聯合似然性：

求得引數結果：

Φi|y=1的分子為標記為1的郵件中出現詞j的郵件數目和，分母為垃圾郵件數，總體意義就是訓練集中出現詞j的垃圾郵件在垃圾郵件中的比例。

Φi|y=0就是出現詞j的非垃圾郵件在非垃圾郵件中的比例。

Φy就是垃圾郵件在所有郵件中的比例。

求出上述引數，就知道了p(x|y)和p(y)，用伯努利分佈對p(y)建模，用上式中p(xi|y)的乘積對p(x|y)建模，通過貝葉斯公式就可求得p(y|x)

*實際操作中，例如將最近兩個月的郵件都標記上“垃圾”或“非垃圾”，然後得到(x(1),y(1))…(x(m),y(m))，x(i)為詞向量，標記出現在第i個郵件中的詞，y(i)為第i個郵件是否是垃圾郵件。用郵件中的所有出現的詞構造字典，或者選擇出現次數k次以上的詞構造字典。

樸素貝葉斯的問題：

設有一封新郵件中出現一個字典沒有的新詞，設其標號為30000，因為這個詞在垃圾郵件和非垃圾郵件中都不存在，則p(x3000|y=1)=0，p(x30000|y=0)=0，計算p(y=1|x)如下：

p(y=1|x) = p(x|y=1)p(y=1) / ( p(x|y=1)p(y=1) + p(x|y=0)p(y=0))

由於p(x|y=1)=p(x|y=0)=0（p(x30000|y=1)=p(x30000|y=0)=0，則乘積為0），則p(y=1|x)=0/0，則結果是未定義的。

其問題在於，統計上認為p(x30000|y)=0是不合理的。即在過去兩個月郵件裡未出現過這個詞，就認為其出現概率為0，並不合理。

概括來講，即之前沒有見過的事件，就認為這些事件不會發生，是不合理的。通過Laplace平滑解決這個問題。

4、 Laplace平滑

根據極大似然估計，p(y=1) = #”1”s / (#”0”s + #”1”s)，即y為1的概率是樣本中1的數目在所有樣本中的比例。Laplace平滑就是將分子分母的每一項都加1,，即：

p(y=1) = (#”1”s+1)  / (#”0”s+1 + #”1”s+1)

例：給出一支球隊5場比賽的結果作為樣本，5場比賽都輸了，記為0，那麼要預測第六場比賽的勝率，按照樸素貝葉斯為：p(y=1) = 0/(5+0) = 0，即樣本中沒有勝場，則勝率為0，顯然這是不合理的。按照Laplace平滑處理，p(y=1) = 0+1/(5+1+0+1) = 1/7，並不為0，且隨著負場次的增加，p(y=1)會一直減小，但不會為0。

更一般的，若y取k中可能的值，比如嘗試估計多項式分佈的引數，得到下式：

即值為j的樣本所佔比例，對其用Laplace平滑如下式：

對於樸素貝葉斯，得到的結果為：

在分子上加1，分母上加2，解決了0概率的問題。