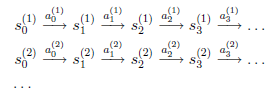【機器學習-斯坦福】學習筆記21——增強學習(Reinforcement Learning and Control)
在之前的討論中,我們總是給定一個樣本x,然後給或者不給label y。之後對樣本進行擬合、分類、聚類或者降維等操作。然而對於很多序列決策或者控制問題,很難有這麼規則的樣本。比如,四足機器人的控制問題,剛開始都不知道應該讓其動那條腿,在移動過程中,也不知道怎麼讓機器人自動找到合適的前進方向。
另外如要設計一個下象棋的AI,每走一步實際上也是一個決策過程,雖然對於簡單的棋有A*的啟發式方法,但在局勢複雜時,仍然要讓機器向後面多考慮幾步後才能決定走哪一步比較好,因此需要更好的決策方法。
對於這種控制決策問題,有這麼一種解決思路。我們設計一個回報函式(reward function),如果learning agent(如上面的四足機器人、象棋AI程式)在決定一步後,獲得了較好的結果,那麼我們給agent一些回報(比如回報函式結果為正),得到較差的結果,那麼回報函式為負。比如,四足機器人,如果他向前走了一步(接近目標),那麼回報函式為正,後退為負。如果我們能夠對每一步進行評價,得到相應的回報函式,那麼就好辦了,我們只需要找到一條回報值最大的路徑(每步的回報之和最大),就認為是最佳的路徑。
增強學習在很多領域已經獲得成功應用,比如自動直升機,機器人控制,手機網路路由,市場決策,工業控制,高效網頁索引等。
接下來,先介紹一下馬爾科夫決策過程(MDP,Markov decision processes)。
1. 馬爾科夫決策過程
* S表示狀態集(states)。(比如,在自動直升機系統中,直升機當前位置座標組成狀態集)
* A表示一組動作(actions)。(比如,使用控制桿操縱的直升機飛行方向,讓其向前,向後等)
* ![]() 是狀態轉移概率。S中的一個狀態到另一個狀態的轉變,需要A來參與。
是狀態轉移概率。S中的一個狀態到另一個狀態的轉變,需要A來參與。![]() 表示的是在當前
表示的是在當前![]() 狀態下,經過
狀態下,經過![]() 作用後,會轉移到的其他狀態的概率分佈情況(當前狀態執行a後可能跳轉到很多狀態)。
作用後,會轉移到的其他狀態的概率分佈情況(當前狀態執行a後可能跳轉到很多狀態)。
* ![]() ,R是回報函式(reward
function),回報函式經常寫作S的函式(只與S有關),這樣的話,R重新寫作
,R是回報函式(reward
function),回報函式經常寫作S的函式(只與S有關),這樣的話,R重新寫作![]() 。
。
MDP的動態過程如下:某個agent的初始狀態為![]() ,然後從A中挑選一個動作
,然後從A中挑選一個動作![]() 執行,執行後,agent按
執行,執行後,agent按![]() 概率隨機轉移到了下一個
概率隨機轉移到了下一個![]() 狀態,
狀態,![]() 。然後再執行一個動作
。然後再執行一個動作![]() ,就轉移到了
,就轉移到了![]() ,接下來再執行
,接下來再執行![]() …,我們可以用下面的圖表示整個過程
…,我們可以用下面的圖表示整個過程
如果對HMM有了解的話,理解起來比較輕鬆。
我們定義經過上面轉移路徑後,得到的回報函式之和如下
如果R只和S有關,那麼上式可以寫作
我們的目標是選擇一組最佳的action,使得全部的回報加權和期望最大。
從上式可以發現,在t時刻的回報值被打了![]() 的折扣,是一個逐步衰減的過程,越靠後的狀態對回報和影響越小。最大化期望值也就是要將大的
的折扣,是一個逐步衰減的過程,越靠後的狀態對回報和影響越小。最大化期望值也就是要將大的![]() 儘量放到前面,小的儘量放到後面。
儘量放到前面,小的儘量放到後面。
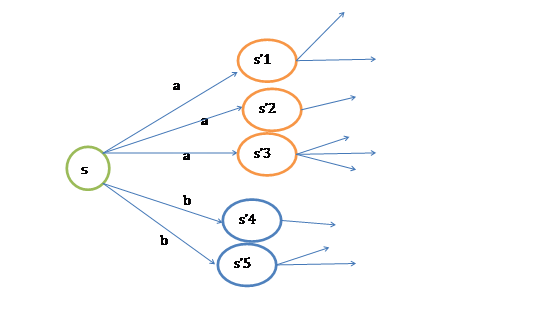
已經處於某個狀態s時,我們會以一定策略![]() 來選擇下一個動作a執行,然後轉換到另一個狀態s’。我們將這個動作的選擇過程稱為策略(policy),每一個policy其實就是一個狀態到動作的對映函式
來選擇下一個動作a執行,然後轉換到另一個狀態s’。我們將這個動作的選擇過程稱為策略(policy),每一個policy其實就是一個狀態到動作的對映函式![]() 。給定
。給定![]() 也就給定了
也就給定了![]() ,也就是說,知道了
,也就是說,知道了![]() 就知道了每個狀態下一步應該執行的動作。
就知道了每個狀態下一步應該執行的動作。
我們為了區分不同![]() 的好壞,並定義在當前狀態下,執行某個策略
的好壞,並定義在當前狀態下,執行某個策略![]() 後,出現的結果的好壞,需要定義值函式(value
function)也叫折算累積回報(discounted cumulative reward)
後,出現的結果的好壞,需要定義值函式(value
function)也叫折算累積回報(discounted cumulative reward)
可以看到,在當前狀態s下,選擇好policy後,值函式是回報加權和期望。這個其實很容易理解,給定![]() 也就給定了一條未來的行動方案,這個行動方案會經過一個個的狀態,而到達每個狀態都會有一定回報值,距離當前狀態越近的其他狀態對方案的影響越大,權重越高。這和下象棋差不多,在當前棋局
也就給定了一條未來的行動方案,這個行動方案會經過一個個的狀態,而到達每個狀態都會有一定回報值,距離當前狀態越近的其他狀態對方案的影響越大,權重越高。這和下象棋差不多,在當前棋局![]() 下,不同的走子方案是
下,不同的走子方案是![]() ,我們評價每個方案依靠對未來局勢(
,我們評價每個方案依靠對未來局勢(![]() ,
,![]() ,…)的判斷。一般情況下,我們會在頭腦中多考慮幾步,但是我們會更看重下一步的局勢。
,…)的判斷。一般情況下,我們會在頭腦中多考慮幾步,但是我們會更看重下一步的局勢。
從遞推的角度上考慮,當期狀態s的值函式V,其實可以看作是當前狀態的回報R(s)和下一狀態的值函式V’之和,也就是將上式變為:
然而,我們需要注意的是雖然給定![]() 後,在給定狀態s下,a是唯一的,但
後,在給定狀態s下,a是唯一的,但![]() 可能不是多到一的對映。比如你選擇a為向前投擲一個骰子,那麼下一個狀態可能有6種。再由Bellman等式,從上式得到
可能不是多到一的對映。比如你選擇a為向前投擲一個骰子,那麼下一個狀態可能有6種。再由Bellman等式,從上式得到
s’表示下一個狀態。
前面的R(s)稱為立即回報(immediate reward),就是R(當前狀態)。第二項也可以寫作![]() ,是下一狀態值函式的期望值,下一狀態s’符合
,是下一狀態值函式的期望值,下一狀態s’符合![]() 分佈。
分佈。
可以想象,當狀態個數有限時,我們可以通過上式來求出每一個s的V(終結狀態沒有第二項V(s’))。如果列出線性方程組的話,也就是|S|個方程,|S|個未知數,直接求解即可。
當然,我們求V的目的就是想找到一個當前狀態s下,最優的行動策略![]() ,定義最優的V*如下:
,定義最優的V*如下:
就是從可選的策略![]() 中挑選一個最優的策略(discounted
rewards最大)。
中挑選一個最優的策略(discounted
rewards最大)。
上式的Bellman等式形式如下:
第一項與![]() 無關,所以不變。第二項是一個
無關,所以不變。第二項是一個![]() 就決定了每個狀態s的下一步動作a,執行a後,s’按概率分佈的回報概率和的期望。
就決定了每個狀態s的下一步動作a,執行a後,s’按概率分佈的回報概率和的期望。
如果上式還不好理解的話,可以參考下圖:
根據以上式子,我們可以知道
解釋一下就是當前狀態的最優的值函式V*,是由採用最優執行策略![]() 的情況下得出的,採用最優執行方案的回報顯然要比採用其他的執行策略
的情況下得出的,採用最優執行方案的回報顯然要比採用其他的執行策略![]() 要好。
要好。
這裡需要注意的是,如果我們能夠求得每個s下最優的a,那麼從全域性來看,![]() 的對映即可生成,而生成的這個對映是最優對映,稱為
的對映即可生成,而生成的這個對映是最優對映,稱為![]() 。
。![]() 針對全域性的s,確定了每一個s的下一個行動a,不會因為初始狀態s選取的不同而不同。
針對全域性的s,確定了每一個s的下一個行動a,不會因為初始狀態s選取的不同而不同。
2. 值迭代和策略迭代法
上節我們給出了迭代公式和優化目標,這節討論兩種求解有限狀態MDP具體策略的有效演算法。這裡,我們只針對MDP是有限狀態、有限動作的情況,![]() 。
。
* 值迭代法
|
1、 將每一個s的V(s)初始化為0 2、 迴圈直到收斂 { 對於每一個狀態s,對V(s)做更新 } |
值迭代策略利用了上節中公式(2)
內迴圈的實現有兩種策略:
1、 同步迭代法
拿初始化後的第一次迭代來說吧,初始狀態所有的V(s)都為0。然後對所有的s都計算新的V(s)=R(s)+0=R(s)。在計算每一個狀態時,得到新的V(s)後,先存下來,不立即更新。待所有的s的新值V(s)都計算完畢後,再統一更新。
這樣,第一次迭代後,V(s)=R(s)。
2、 非同步迭代法
與同步迭代對應的就是非同步迭代了,對每一個狀態s,得到新的V(s)後,不儲存,直接更新。這樣,第一次迭代後,大部分V(s)>R(s)。
不管使用這兩種的哪一種,最終V(s)會收斂到V*(s)。知道了V*後,我們再使用公式(3)來求出相應的最優策略![]() ,當然
,當然![]() 可以在求V*的過程中求出。
可以在求V*的過程中求出。
* 策略迭代法
|
2、 迴圈直到收斂 { } |
(a)步中的V可以通過之前的Bellman等式求得
(b)步實際上就是根據(a)步的結果挑選出當前狀態s下,最優的a,然後對![]() 做更新。
做更新。
對於值迭代和策略迭代很難說哪種方法好,哪種不好。對於規模比較小的MDP來說,策略一般能夠更快地收斂。但是對於規模很大(狀態很多)的MDP來說,值迭代比較容易(不用求線性方程組)。
3. MDP中的引數估計
在之前討論的MDP中,我們是已知狀態轉移概率![]() 和回報函式R(s)的。但在很多實際問題中,這些引數不能顯式得到,我們需要從資料中估計出這些引數(通常S、A和
和回報函式R(s)的。但在很多實際問題中,這些引數不能顯式得到,我們需要從資料中估計出這些引數(通常S、A和![]() 是已知的)。
是已知的)。
假設我們已知很多條狀態轉移路徑如下:
其中,![]() 是i時刻,第j條轉移路徑對應的狀態,
是i時刻,第j條轉移路徑對應的狀態,![]() 是
是![]() 狀態時要執行的動作。每個轉移路徑中狀態數是有限的,在實際操作過程中,每個轉移鏈要麼進入終結狀態,要麼達到規定的步數就會終結。
狀態時要執行的動作。每個轉移路徑中狀態數是有限的,在實際操作過程中,每個轉移鏈要麼進入終結狀態,要麼達到規定的步數就會終結。
如果我們獲得了很多上面類似的轉移鏈(相當於有了樣本),那麼我們就可以使用最大似然估計來估計狀態轉移概率。
分子是從s狀態執行動作a後到達s’的次數,分母是在狀態s時,執行a的次數。兩者相除就是在s狀態下執行a後,會轉移到s’的概率。
為了避免分母為0的情況,我們需要做平滑。如果分母為0,則令![]() ,也就是說當樣本中沒有出現過在s狀態下執行a的樣例時,我們認為轉移概率均分。
,也就是說當樣本中沒有出現過在s狀態下執行a的樣例時,我們認為轉移概率均分。
上面這種估計方法是從歷史資料中估計,這個公式同樣適用於線上更新。比如我們新得到了一些轉移路徑,那麼對上面的公式進行分子分母的修正(加上新得到的count)即可。修正過後,轉移概率有所改變,按照改變後的概率,可能出現更多的新的轉移路徑,這樣![]() 會越來越準。
會越來越準。
同樣,如果回報函式未知,那麼我們認為R(s)為在s狀態下已經觀測到的回報均值。
當轉移概率和回報函式估計出之後,我們可以使用值迭代或者策略迭代來解決MDP問題。比如,我們將引數估計和值迭代結合起來(在不知道狀態轉移概率情況下)的流程如下:
|
2、 迴圈直到收斂 { (b) 使用估計到的引數來更新V(使用上節的值迭代方法) } |
在(b)步中我們要做值更新,也是一個迴圈迭代的過程,在上節中,我們通過將V初始化為0,然後進行迭代來求解V。巢狀到上面的過程後,如果每次初始化V為0,然後迭代更新,就會很慢。一個加快速度的方法是每次將V初始化為上一次大迴圈中得到的V。也就是說V的初值銜接了上次的結果。
4. 總結
首先我們這裡討論的MDP是非確定的馬爾科夫決策過程,也就是回報函式和動作轉換函式是有概率的。在狀態s下,採取動作a後的轉移到的下一狀態s’也是有概率的。再次,在增強學習裡有一個重要的概念是Q學習,本質是將與狀態s有關的V(s)轉換為與a有關的Q。強烈推薦Tom Mitchell的《機器學習》最後一章,裡面介紹了Q學習和更多的內容。最後,裡面提到了Bellman等式,在《演算法導論》中有Bellman-Ford的動態規劃演算法,可以用來求解帶負權重的圖的最短路徑,裡面最值得探討的是收斂性的證明,非常有價值。有學者仔細分析了增強學習和動態規劃的關係。
這篇是ng講義中最後一篇了,還差一篇learning theory,暫時不打算寫了,感覺對learning的認識還不深。等到學習完圖模型和線上學習等內容後,再回過頭來寫learning theory吧。另外,ng的講義中還有一些數學基礎方面的講義比如概率論、線性代數、凸優化、高斯過程、HMM等,都值得看一下。