opencv學習筆記:RotatedRect和CvBox2D的角度疑雲
在使用opencv的過程中經常會使用minAreaRect返回一個輪廓的外接矩形,它返回的是一個RotatedRect的類:
class CV_EXPORTS RotatedRect { public: //! various constructors RotatedRect(); RotatedRect(const Point2f& center, const Size2f& size, float angle); RotatedRect(const CvBox2D& box); //! returns 4 vertices of the rectangle void points(Point2f pts[]) const; //! returns the minimal up-right rectangle containing the rotated rectangle Rect boundingRect() const; //! conversion to the old-style CvBox2D structure operator CvBox2D() const; Point2f center; //< the rectangle mass center Size2f size; //< width and height of the rectangle float angle; //< the rotation angle. When the angle is 0, 90, 180, 270 etc., the rectangle becomes an up-right rectangle. };
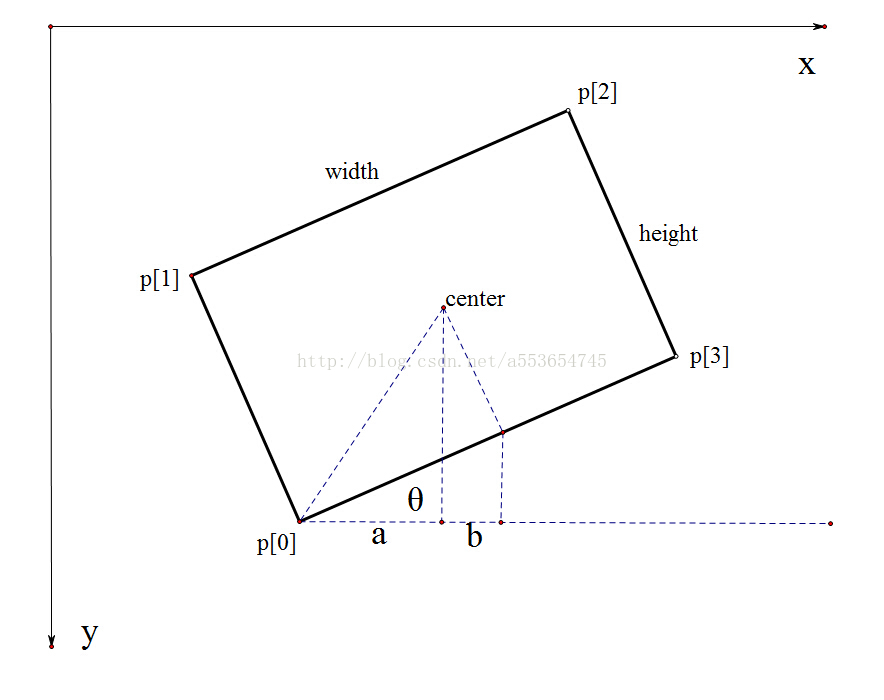
這個類中包含了外接矩形的中心center、大小size以及角度angle。為了更好的理解這幾個引數的意義,請看下圖:
在opencv中,座標的原點在左上角,與x軸平行的方向為角度為0,逆時針旋轉角度為負,順時針旋轉角度為正。而RotatedRect類是以矩形的哪一條邊與x軸的夾角作為角度的呢?參考http://blog.csdn.net/mine1024/article/details/6044856的觀點:angle 是水平軸(x軸)逆時針旋轉,與碰到的第一個邊的夾角,而opencv預設把這個邊的邊長作為width。由前面所說,angle的取值範圍必然是負的,實際angle的取值範圍為(-90,0]。利用成員函式void points(Point2f pts[]) const;可以計算出矩形的四個角點。計算的原理很簡單:
圖中的θ=-angle。從圖中可知p[0].x=center.x-a
其中a=0.5*width*cosθ - b, b=heigth*sinθ,且cosθ=cos(angle),sinθ=sin(-angle)=-sin(angle)
那麼p[0].x=center.x - 0.5*(width*cos(angle) + heigth*sin(angle)),對於p[0].y也可以用同樣的原理計算,對應opencv中的原始碼如下:
void RotatedRect::points(Point2f pt[]) const { double _angle = angle*CV_PI/180.; float b = (float)cos(_angle)*0.5f; float a = (float)sin(_angle)*0.5f; pt[0].x = center.x - a*size.height - b*size.width; pt[0].y = center.y + b*size.height - a*size.width; pt[1].x = center.x + a*size.height - b*size.width; pt[1].y = center.y - b*size.height - a*size.width; pt[2].x = 2*center.x - pt[0].x; pt[2].y = 2*center.y - pt[0].y; pt[3].x = 2*center.x - pt[1].x; pt[3].y = 2*center.y - pt[1].y; }
由此可知道,在opencv中,RotatedRect的角度實際上就是水平軸x與矩形寬width的夾角,而在利用minAreaRect函式去求一個外接矩形時,函式對於矩形長和寬的選擇取決於這個外接矩形的邊與水平軸的角度距離,即將水平軸逆時針旋轉,最先與其平行的邊的長度作為寬度width,另外一條邊則為height,而角度則直接取該邊與水平軸的夾角。應該意識到,在minAreaRect函式中,RotatedRect的width和height的選取跟矩形的尺寸無關,並非長的就是height,短的就是width。