R語言主成分和因子分析篇
主成分分析(PCA)是一種資料降維技巧,它能將大量相關變數轉化為一組很少的不相關變數,這些無關變數稱為主成分。
探索性因子分析(EFA)是一系列用來發現一組變數的潛在結構的方法,通過尋找一組更小 的、潛在的或隱藏的結構來解釋已觀測到的、變數間的關係。
1.R中的主成分和因子分析
R的基礎安裝包中提供了PCA和EFA的函式,分別為princomp ()和factanal()
psych包中有用的因子分析函式
| 函式 | 描述 |
| principal() | 含多種可選的方差放置方法的主成分分析 |
| fa() | 可用主軸、最小殘差、加權最小平方或最大似然法估計的因子分析 |
| fa.parallel() | 含平等分析的碎石圖 |
| factor.plot() | 繪製因子分析或主成分分析的結果 |
| fa.diagram() | 繪製因子分析或主成分分析的載荷矩陣 |
| scree() | 因子分析和主成分分析的碎石圖 |
(1)資料預處理;PCA和EFA都是根據觀測變數間的相關性來推導結果。使用者可以輸入原始資料矩陣或相關係數矩陣列到principal()和fa()函式中,若輸出初始結果,相關係數矩陣將會被自動計算,在計算前請確保資料中沒有缺失值;
(2)選擇因子分析模型。判斷是PCA(資料降維)還是EFA(發現潛在結構)更符合你的分析目標。若選擇EFA方法時,還需要選擇一種估計因子模型的方法(如最大似然估計)。
(3)判斷要選擇的主成分/因子數目;
(4)選擇主成分/因子;
(5)旋轉主成分/因子;
(6)解釋結果;
(7)計算主成分或因子得分。
2.主成分分析
PCA的目標是用一組較少的不相關變數代替大量相關變數,同時儘可能保留初始變數的資訊,這些推導所得的變數稱為主成分,它們是觀測變數的線性組合。如第一主成分為:
PC1=a1X1=a2X2+……+akXk 它是k個觀測變數的加權組合,對初始變數集的方差解釋性最大。
第二主成分是初始變數的線性組合,對方差的解釋性排第二, 同時與第一主成分正交(不相關)。後面每一個主成分都最大化它對方差的解釋程度,同時與之前所有的主成分都正交,但從實用的角度來看,都希望能用較少的主成分來近似全變數集。
(1)判斷主成分的個數
PCA中需要多少個主成分的準則:
根據先驗經驗和理論知識判斷主成分數;
根據要解釋變數方差的積累值的閾值來判斷需要的主成分數;
通過檢查變數間k*k的相關係數矩陣來判斷保留的主成分數。
最常見的是基於特徵值的方法,每個主成分都與相關係數矩陣的特徵值 關聯,第一主成分與最大的特徵值相關聯,第二主成分與第二大的特徵值相關聯,依此類推。
Kaiser-Harris準則建議保留特徵值大於1的主成分,特徵值小於1的成分所解釋的方差比包含在單個變數中的方差更少。
Cattell碎石檢驗則繪製了特徵值與主成分數的圖形,這類圖形可以展示圖形彎曲狀況,在圖形變化最大處之上的主成分都保留。
最後,還可以進行模擬,依據與初始矩陣相同大小的隨機數矩陣來判斷要提取的特徵值。若基於真實資料的某個特徵值大於一組隨機資料矩陣相應的平均特徵值,那麼該主成分可以保留。該方法稱作平行分析。
利用fa.parallel()函式,可同時對三種特徵值判別準則進行評價。
library(psych)
fa.parallel(USJudgeRatings[,-1],fa="PC",n.iter=100,show.legend=FALSE,main="Screen plot with parallel analysis")
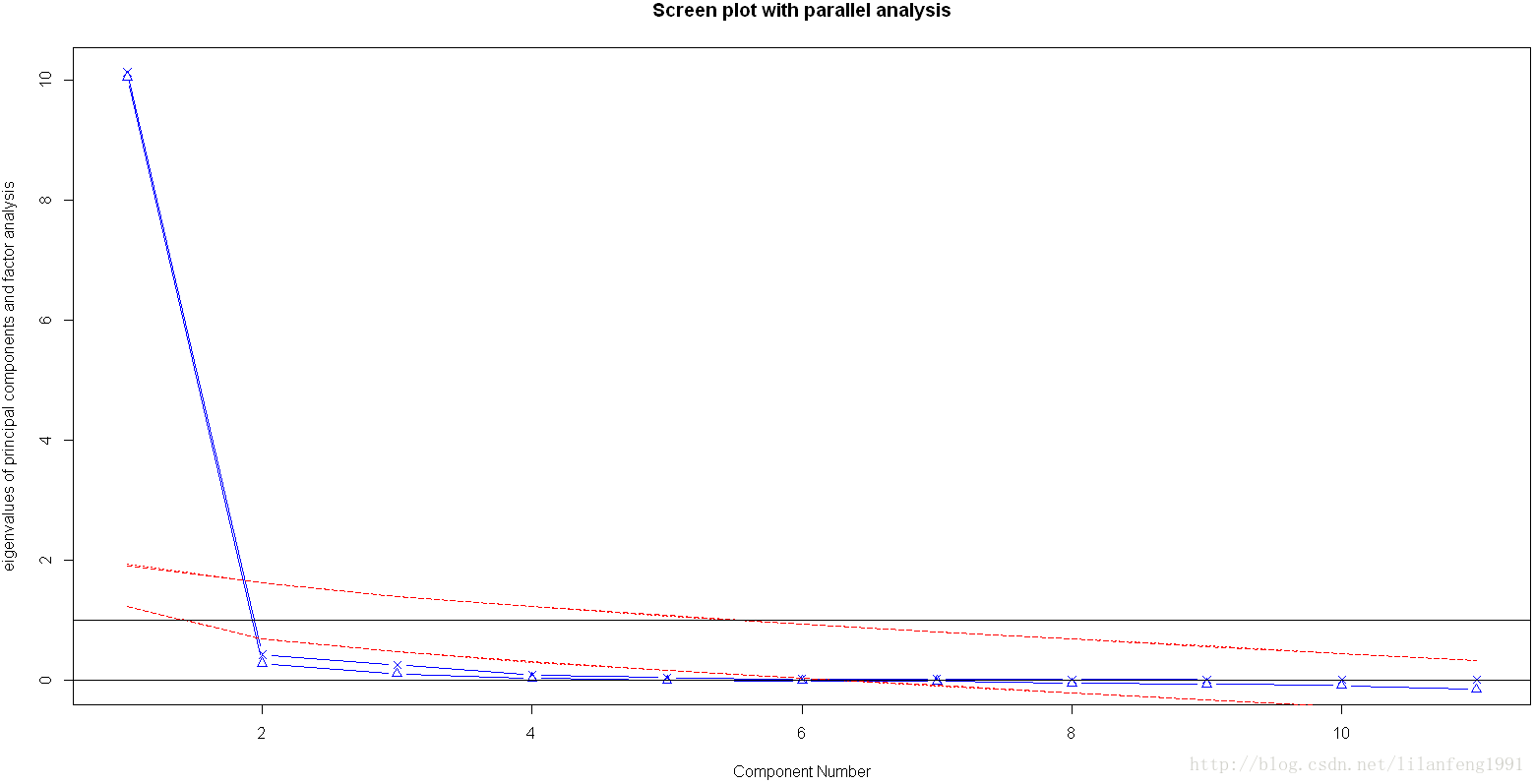
碎石頭、特徵值大於1準則和100次模擬的平行分析(虛線)都表明保留一個主成分即可保留資料集的大部分資訊,下一步是使用principal()函式挑選出相應的主成分。
(2)提取主成分
principal()函式可根據原始資料矩陣或相關係數矩陣做主成分分析
格式為:principal(的,nfactors=,rotate=,scores=)
其中:r是相關係數矩陣或原始資料矩陣;
nfactors設定主成分數(預設為1);
rotate指定旋轉的方式[預設最大方差旋轉(varimax)]
scores設定是否需要計算主成分得分(預設不需要)。
美國法官評分的主成分分析
library(psych)
pc<-principal(USJudgeRatings[,-1],nfactors=1)
pc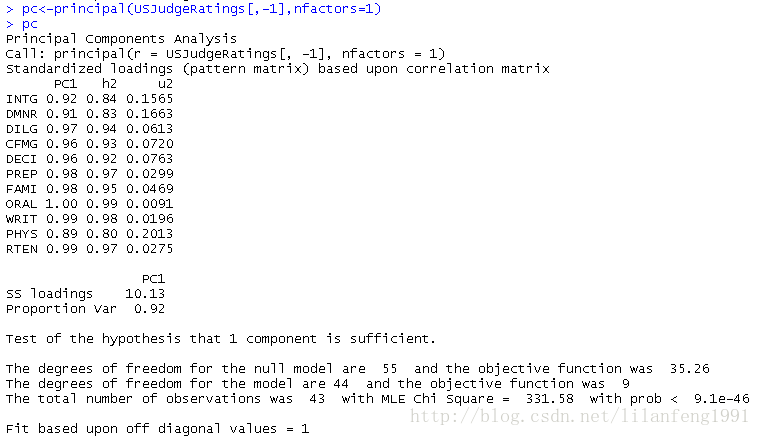
此處,輸入的是沒有ONT變數的原始,並指定獲取一個未旋轉的主成分。由於PCA只對相關係數矩陣進行分析,在獲取主成分前,原始資料將會被自動轉換為相關係數矩陣。
PC1欄包含了成分載荷,指觀測變數與主成分的相關係數。如果提取不止一個主成分,則還將會有PC2、PC3等欄。成分載荷(component loadings)可用來解釋主成分的含義。此處可看到,第一主成分(PC1)與每個變數都高度相關,也就是說,它是一個可用來進行一般性評價的維度。
h2柆指成分公因子方差-----主成分對每個變數的方差解釋度。
u2欄指成分唯一性-------方差無法 被主成分解釋的比例(1-h2)。
SS loadings行包含了主成分相關聯的特徵值,指的是與特定主成分相關聯的標準化後的方差值。
Proportin Var行表示的是每個主成分對整個資料集的解釋程度。
結果不止一個主成分的情況
library(psych)
fa.parallel(Harman23.cor$cov,n.obs=302,fa="pc",n.iter=100,show.legend=FALSE,main="Scree plot with parallel analysis")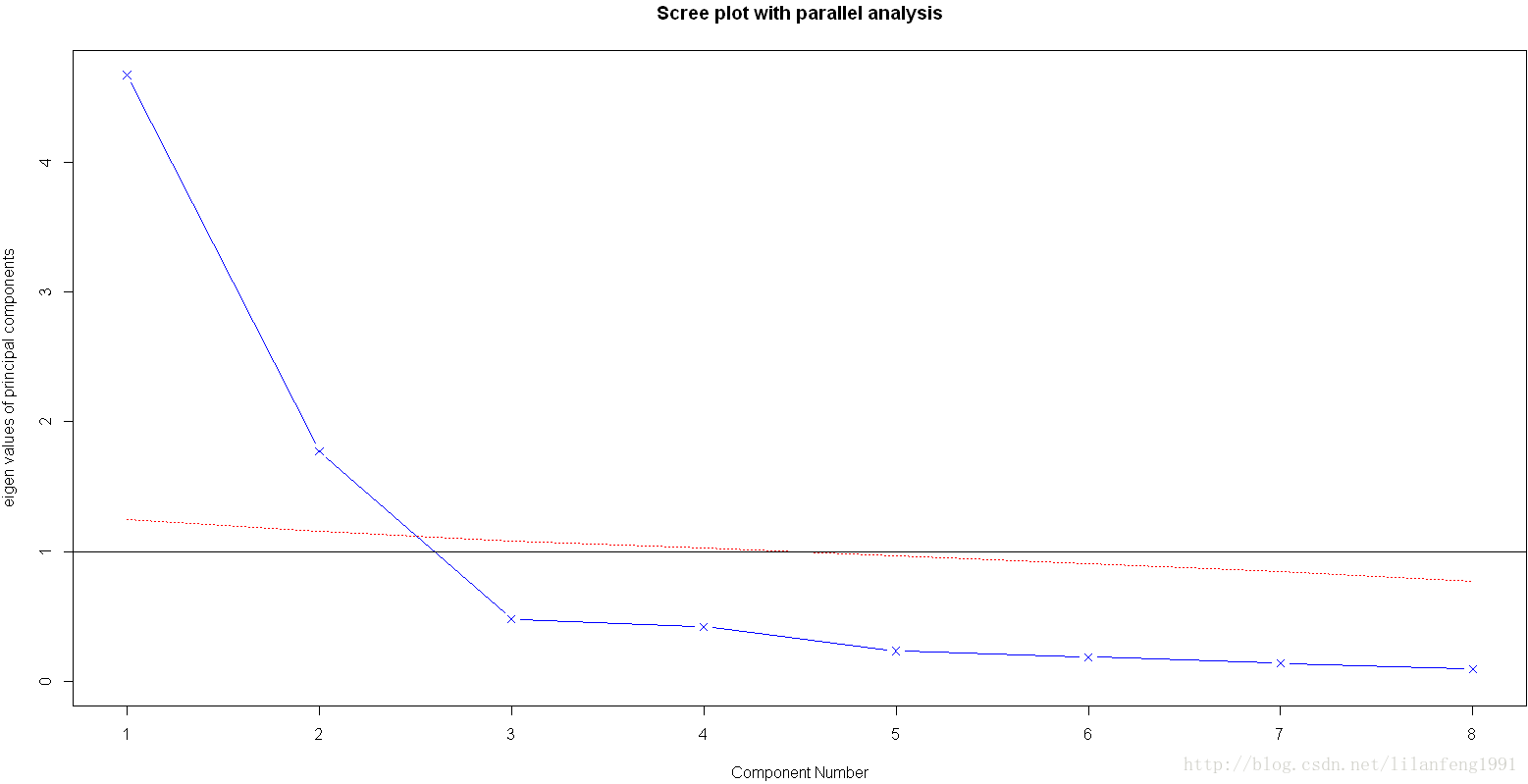
載荷陣解釋了成分和因子的含義,第一成分與每個身體測量指標都正相關,看起來似乎是一個一般性的衡量因子;第二主成分與前四個變數負相關,與後四個變數正相關,因此它看起來似乎是一個長度容量因子。但理念上的東西都不容易構建,當提取了多個成分時,對它們進行旋轉可使結果更具有解釋性。
(3)主成分旋轉
旋轉是一系列將成分載荷陣變得更容易解釋的數學方法,它們儘可能地對成分去噪。
旋轉方法有兩種:使選擇的成分保持不相關(正效旋轉),和讓它們變得相關(斜交旋轉)。
旋轉方法也會依據去噪定義的不同而不同。
最流行的下次旋轉是方差極大旋轉,它試圖對載荷陣的列進行去噪,使得每個成分只是由一組有限的變數來解釋(即載荷陣每列只有少數幾個很大的載荷,其他都是很小的載荷)。
install.packages("GPArotation")
library(GPArotation)
rc<-principal(Harman23.cor$cov,nfactors=2,rotate="varimax")
rc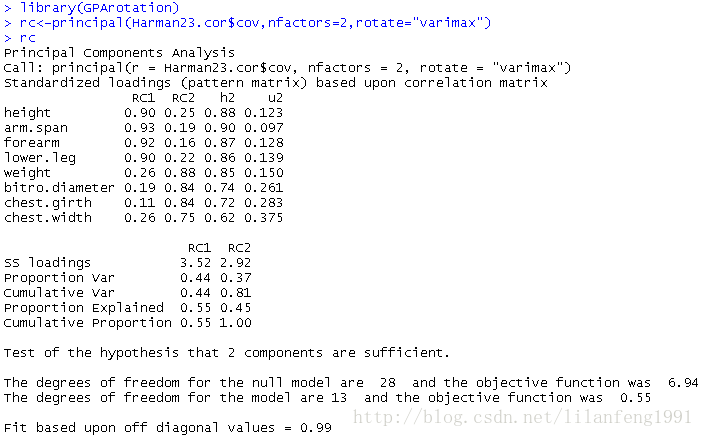
列名從PC變成了RC,以表示成分被旋轉
觀察可以發現第一主成分主要由前四個變數來解釋,第二主成分主要由變數5到變數8來解釋。
注意兩個主成分仍不相關,對變數的解釋性不變,這是因為變數的群組沒有發生變化。另外,兩個主成分放置後的累積方差解釋性沒有變化,變的只是各個主成分對方差的解釋(成分1從58%變為44%,成分2從22%變為37%)。各成分的方差解釋度趨同,準確來說,此時應該稱它們為成分而不是主成分。
(4)獲取主成分得分
利用principal()函式,很容易獲得每個調查物件在該主成分上的得分。
<strong>從原始資料中獲取成分得分</strong>library(psych)
pc<-principal(USJudgeRatings[,-1],nfactors=1,score=TRUE)
head(pc$scores)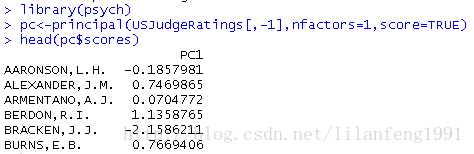
當scores=TRUE時,主成分得分儲存在principal()函式返回物件的scores元素中。
cor(USJudgeRatings$CONT,PC$scores)<strong>獲取主成分得分的係數</strong>library(psych)
rc<-principal(Harman23.cor$cov,nfactor=2,rotate="varimax")
round(unclass(rc$weights),2)

得到主成分得分:
PC1=0.28*height+0.30*arm.span+0.30*forearm+0.29*lower.leg-0.06*weight-0.08*bitro.diameter-0.10*chest.girth-0.04*chest.width
PC2=-0.05*height-0.08*arm.span-0.09*forearm-0.06*lower.leg+0.33*weight+0.32*bitro.diameter+0.34*chest.girth+0.27*chest.width
3.探索性因子分析
EFA的目標是通過發掘隱藏在資料下的一組較少的、更為基本的無法觀測的變數,來解釋一組可觀測變數的相關性。這些虛擬的、無法觀測的變數稱作因子。(每個因子被認為可解釋多個觀測變數間共有的方差,也叫作公共因子) 模型的形式為: Xi=a1F1+a2F2+……apFp+Ui Xi是第i個可觀測變數(i=1,2,……k) Fj是公共因子(j=1,2,……p) 並且p<koptions(digits=2)
covariances<-ability.cov$cov
correlations<-cov2cor(covariances)
correlations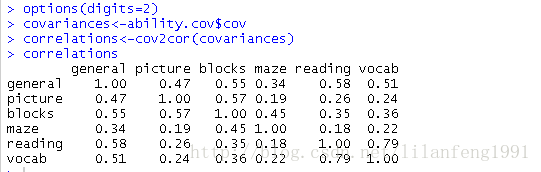
ability.cov提供了變數的協方差矩陣
cov2cor()函式將其轉化為相關係數矩陣
(1)判斷需提取的公共因子數
library(psych)
convariances<-ability.cov$cov
correlations<-cov2cor(covariances)
fa.parallel(correlations,n.obs=112,fa="both",n.iter=100,main="Scree plots with parallel analysis")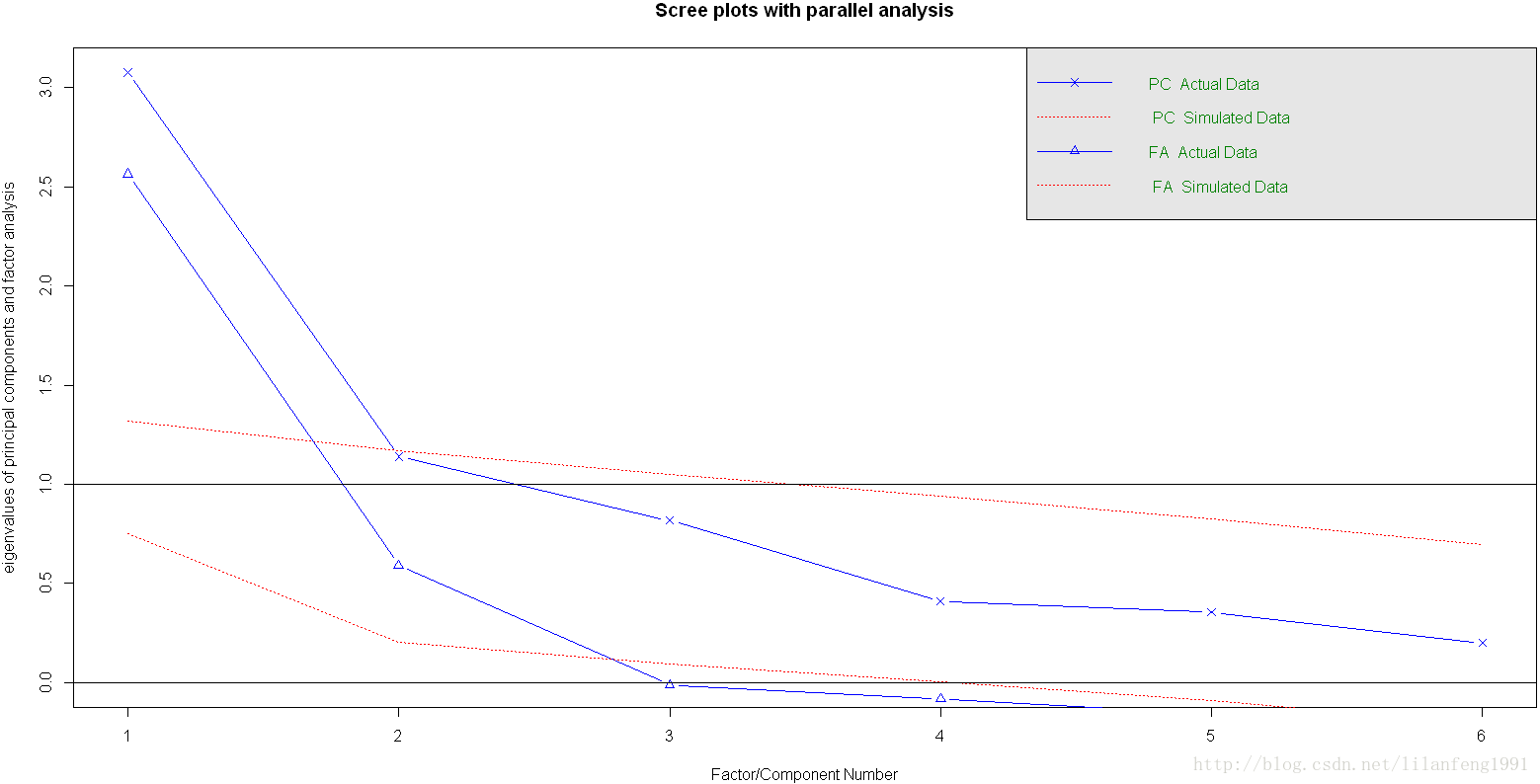
若使用PCA方法,可能會選擇一個成分或兩個成分。當搖擺不定時,高估因子數通常比低估因子數的結果好,因為高估因子數一般較少曲解“真實”情況。
(2)提取公共因子
可使用fa()函式來提取因子 fa()函式的格式為: fa(r,nfactors=,n.obs=,rotate=,scores=,fm) r是相關係數矩陣或原始資料矩陣; nfactors設定提取的因子數(預設為1); n.obs是觀測數(輸入相關係數矩陣時需要填寫); rotate設定放置的方法(預設互變異數最小法); scores設定是否計算因子得分(預設不計算); fm設定因子化方法(預設極小殘差法)。 與PCA不同,提取公共因子的方法很多,包括最大似然法(ml)、主軸迭代法(pa)、加權最小二乘法(wls)、廣義加權最小二乘法(gls)和最小殘差法(minres)。<strong>未旋轉的主軸迭代因子法</strong>fa<-fa(correlations,nfactors=2,rotate="none",fm="pa")
fa
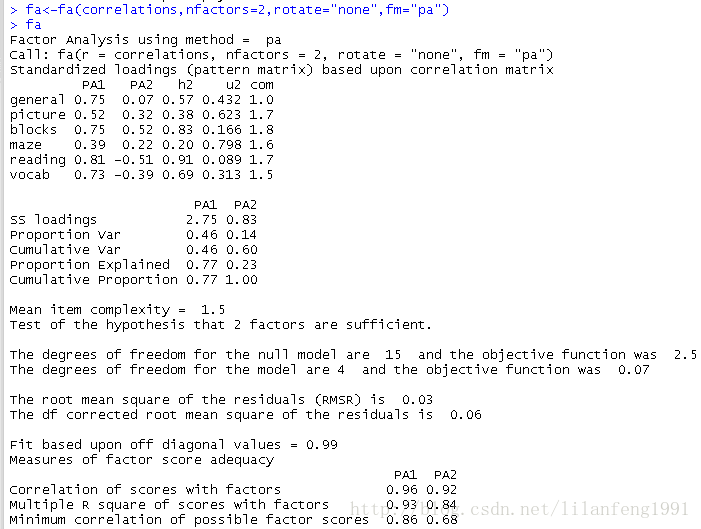
(3)因子旋轉
<strong>用正交旋轉提取因子</strong>fa.varimax<-fa(correlations,nfactors=2,rotate="varimax",fm="pa")
fa.varimax<strong>正交放置將人為地強制兩個因子不相關</strong><strong>正交旋轉,因子分析的重點在於因子結構矩陣(變數與因子的相關係數)</strong>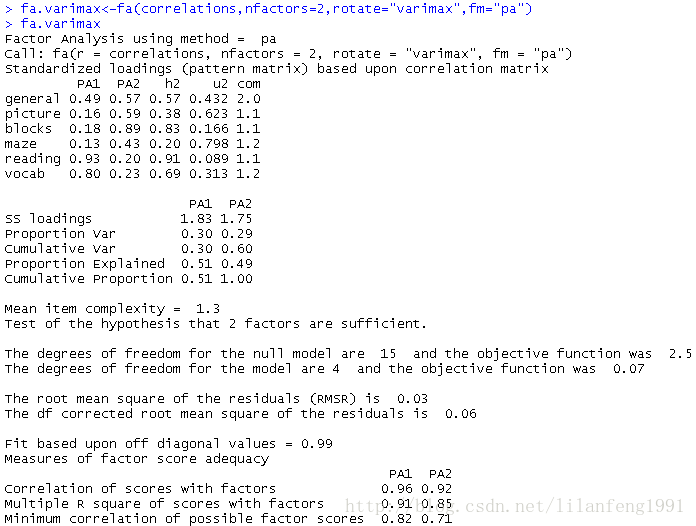
用斜交旋轉提取因子
fa.promax<-fa(correlations,nfactors=2,rotate="promax",fm="pa")
fa.promax
<strong>對於斜交旋轉,因子分析會考慮三個矩陣:因子結構矩陣、因子模式矩陣和因子關聯矩陣</strong><strong>因子模式矩陣即標準化的迴歸係數矩陣,它列出了因子的預測變數的權重;</strong><strong>因子關聯矩陣即因子相關係數矩陣;</strong><strong>因子結構矩陣(或稱因子載荷陣),可使用公式F=P*Phi來計算得到,其中F是載荷陣,P為因子模式矩陣,Phi為因子關聯矩陣。</strong>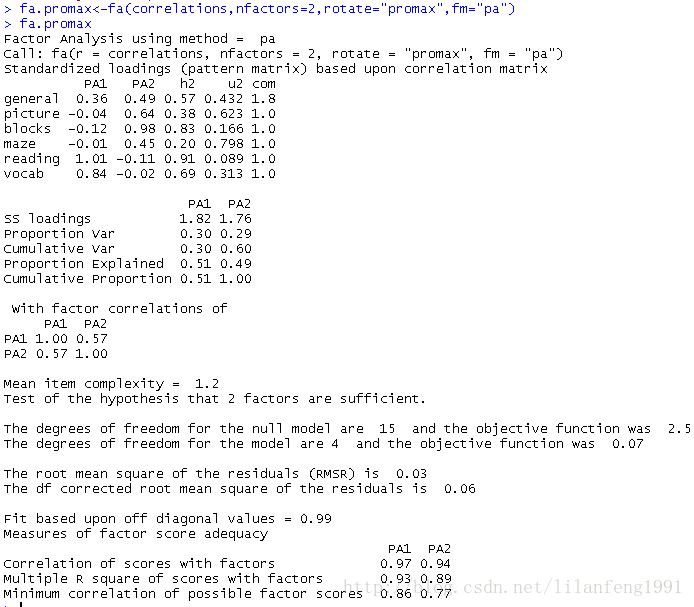
fsm<-function(oblique){
if(class(oblique)[2]=="fa"&is.null(oblique$Phi)){
warning("Object doesn't look like oblique EFA")
}else{
P<-unclass(oblique$loading)
F<-P%*%oblique$Phi
colnames(F)<-c("PA1","PA2")
return (F)
}
}
fsm(fa.promax)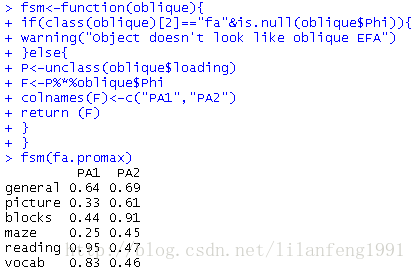 可以看到變數與因子間的相關係數。將它們與正交旋轉所得因子載荷陣相比,發現該載荷陣列的噪音較大,這是因為之前允許潛在因子相關。雖然斜交方法更為複雜,但模型將更加符合真實資料。
使用factor.plot()或fa.diagram()函式,可繪製正交或斜交結果的圖形
可以看到變數與因子間的相關係數。將它們與正交旋轉所得因子載荷陣相比,發現該載荷陣列的噪音較大,這是因為之前允許潛在因子相關。雖然斜交方法更為複雜,但模型將更加符合真實資料。
使用factor.plot()或fa.diagram()函式,可繪製正交或斜交結果的圖形
factor.plot(fa.promax,labels=rownames(fa.promax$loadings))
fa.diagram(fa.promax,simple=TRUE)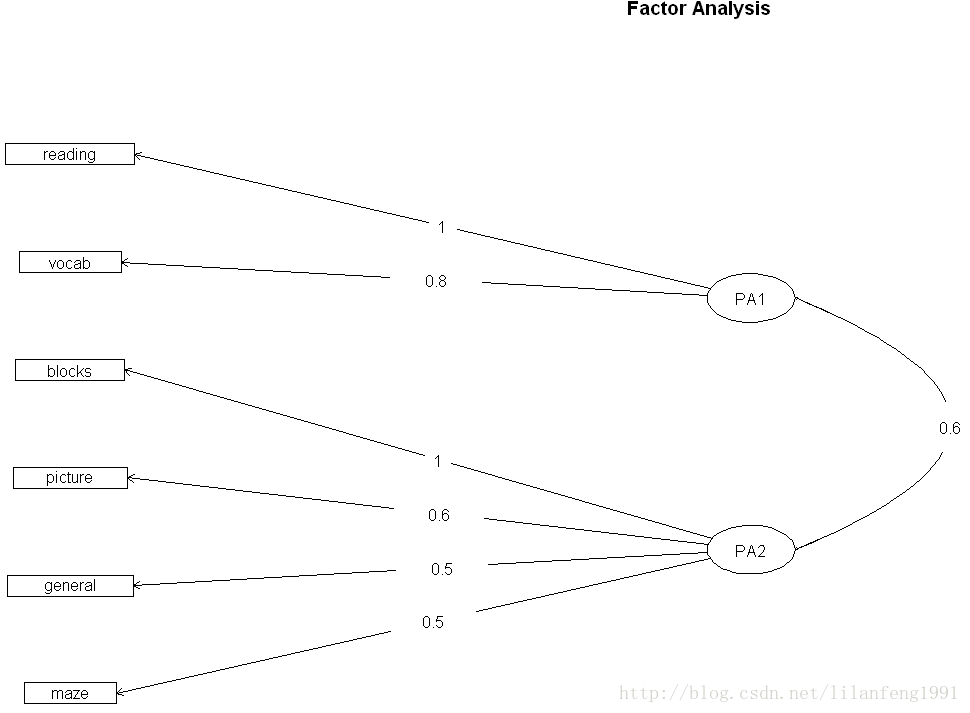
(4)因子得分
EFA並不十分關注因子得分,在fa()函式中新增score=TRUE選項,便可輕鬆地得到因子得分。另外還可以得到得分系數(標準化的迴歸權重),它在返回物件的weights元素中。fa.promax$weights
