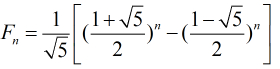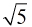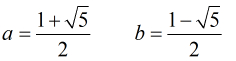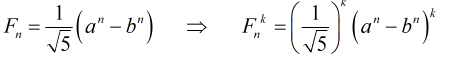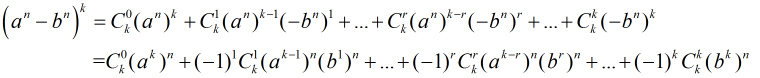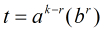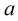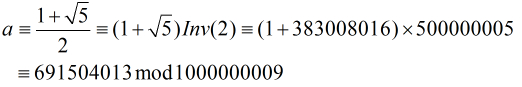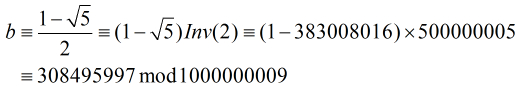題意：給定和，其中，，求的值。

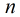
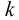
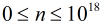
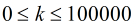
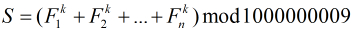
首先k小的情況可以構造矩陣和向量[fi-1^k,fi-1^(k-1)*fi,fi-1^(k-2)*fi^2,....,fi^k,Sum]

#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long ll;

inline char nc(){
  static char buf[100000],*p1=buf,*p2=buf;
  if (p1==p2) { p2=(p1=buf)+fread(buf,1,100000,stdin); if (p1==p2) return EOF; }
  return *p1++;
}

inline void read(int &x){
  char c=nc(),b=1;
  for (;!(c>='0' && c<='9');c=nc()) if (c=='-') b=-1;
  for (x=0;c>='0' && c<='9';x=x*10+c-'0',c=nc()); x*=b;
}

const int M=55;
const int P=1e9+9;

struct Matrix{
  int n;
  ll a[M][M];
  Matrix(){ }
  Matrix(int in,int ii=0){
    n=in; memset(a,0,sizeof(a));
    if (ii) for (int i=0;i<=n;i++) a[i][i]=1;
  }
  ll *operator[](int x){
    return a[x];
  }
  friend Matrix operator* (Matrix A,Matrix B){
    int n=A.n; Matrix ret(n);
    for (int i=0;i<=n;i++)
      for (int j=0;j<=n;j++)
        for (int k=0;k<=n;k++)
	  (ret[i][j]+=A[i][k]*B[k][j]%P)%=P;
    return ret;
  }
}A;


Matrix Pow(Matrix A,int b){
  Matrix ret(A.n,1);
  for (;b;b>>=1,A=A*A)
    if (b&1)
      ret=ret*A;
  return ret; 
}

int n,K;
ll C[M][M];

inline void Pre(){
  C[0][0]=1;
  for (int i=1;i<=K;i++){
    C[i][0]=1;
    for (int j=1;j<=i;j++)
      C[i][j]=(C[i-1][j-1]+C[i-1][j])%P;
  }
}

ll Ans;

int main(){
  freopen("t.in","r",stdin);
  freopen("t.out","w",stdout);
  read(n); read(K); Pre();
  A=Matrix(K+1);
  for (int a=0;a<=K;a++)
    for (int t=0;t<=a;t++)
      A[a][K-a+t]=C[a][t];
  A[K+1][K+1]=A[K+1][K]=1;
  A=Pow(A,n-1);
  for (int i=0;i<=K+1;i++)
    (Ans+=A[K+1][i])%=P;
  printf("%lld\n",Ans);
  return 0;
}
 

以下來自參考博文

分析：嗯，這道題貌似有難度，如果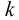比較小的話我們可以構造矩陣，實際上這樣做也挺麻煩的。

     以前我們做一個大Fibonacci數列模一個大素數都是用矩陣，當然這裡素數滿足條件：5是模這個素數的二

     次剩餘，那麼現在要求不要用矩陣來計算這個結果呢？那就是今天我要討論的問題，本題也是基於這種思路。

     本題我們可以直接利用Fibonacci數列的公式進行計算。因為我們知道Fibonacci數列的公式為：

     雖然公式中含有根號，但是我們知道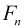是一個整數，而且5是模1000000009的二次剩餘。那麼可以通過逆元

     和二次剩餘的轉化來做。比如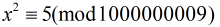

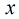
     為了方便表示，我們令：

     那麼得到

     把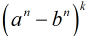按照二項式展開得到

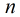
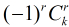
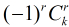
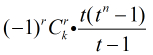
     對於每一個都這樣表示，那麼相同的合併後是等比數列，比如對於所有係數為合併後為

     ， 其中

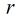
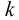
     所以到了這裡本題就明確了，列舉每一個從0到，依次計算即可。

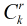
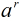
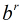
     當然對於，我們可以階乘預處理然後求逆元，至於和同樣預處理，這樣時間少很多。

     可以看出本題條件好在1000000009是素數，而且5是模1000000009的二次剩餘。

     經計算2模1000000009的逆元是500000005，而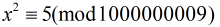的一個解為383008016。

     也就是說對於

     同理，對於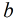有

     嗯，貌似還有一個問題沒有處理，t = 1時咋辦？ 這個很簡單啦，不用等比求和公式即可。其實吧，這裡面

     我們還可以注意到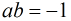，也可以進一步優化，讀者自己體會，就說到這裡。

#include<cstdio>
#include<cstdlib>
#include<algorithm>
using namespace std;
typedef long long ll;

const int P=1000000009;
const int INV2=500000005;
const int SQRT5=383008016;
const int INVSQRT5=276601605;
const int A=691504013;
const int B=308495997;

const int N=100005;

ll n,K;
ll fac[N],inv[N];
ll pa[N],pb[N];

inline void Pre(int n){
  fac[0]=1; for (int i=1;i<=n;i++) fac[i]=fac[i-1]*i%P;
  inv[1]=1; for (int i=2;i<=n;i++) inv[i]=(P-P/i)*inv[P%i]%P;
  inv[0]=1; for (int i=1;i<=n;i++) inv[i]=inv[i]*inv[i-1]%P;
  pa[0]=1; for (int i=1;i<=n;i++) pa[i]=pa[i-1]*A%P;
  pb[0]=1; for (int i=1;i<=n;i++) pb[i]=pb[i-1]*B%P;
}

inline ll C(int n,int m){
  return fac[n]*inv[m]%P*inv[n-m]%P;
}

inline ll Pow(ll a,ll b){
  ll ret=1;
  for (;b;b>>=1,a=a*a%P)
    if (b&1)
      ret=ret*a%P;
  return ret;
}

inline ll Inv(ll x){
  return Pow(x,P-2);
}

inline void Solve(){
  ll Ans=0;
  for (int j=0;j<=K;j++){
    ll t=pa[K-j]*pb[j]%P,tem;
    tem=t==1?n%P:t*(Pow(t,n)-1+P)%P*Inv(t-1)%P;
    if (~j&1)
      Ans+=C(K,j)*tem%P,Ans%=P;
    else
      Ans+=P-C(K,j)*tem%P,Ans%=P;
  }
  Ans=Ans*Pow(INVSQRT5,K)%P;
  printf("%lld\n",Ans);
}

int main(){
  int T;
  freopen("t.in","r",stdin);
  freopen("t.out","w",stdout);
  Pre(100000);
  scanf("%d",&T);
  while (T--){
    scanf("%lld%lld",&n,&K);
    Solve();
  }
}