極大似然

極大似然（Maximum Likelihood）估計為用於已知模型的引數估計的統計學方法。

也就是求使得似然函式最大的代估引數的值。而似然函式就是如果引數已知則已出現樣本出現的概率。

比如，我們想了解拋硬幣是正面（head）的概率分佈θ$\theta$；那麼可以通過最大似然估計方法求得。

θ^=argmaxxl(θ)=argmaxxθ8(1−θ)2$$\hat{\theta }=argma{x}_{x}l(\theta )=argma{x}_x{\theta }^8(1-\theta {)}^2$$

其中，l(θ)$l(\theta )$為觀測變數序列的似然函式。

所以最大似然方法估計引數，就是先假設引數已知，然後用引數，求出樣本出現的概率。如果是多個樣本，就是多個樣本的聯合概率最大

求解使似然函式最大的代估引數，常規的做法就是對似然函式求導，求使導數為0的自變數的值，以及左右邊界線的值。

例如

對l(θ)$l(\theta )$求偏導

∂l(θ)∂θ=θ7(1−θ)(8−10θ)⇒θ^=0.8$$\frac{\partial l(\theta )}{\partial \theta }={\theta }^7(1-\theta )(8-10\theta )\Rightarrow \hat{\theta }=0.8$$

但是如果似然函式不是凹函式（concave），求解極大值困難。一般地，使用與之具有相同單調性的log-likelihood，如圖所示也就是將似然函式求log。

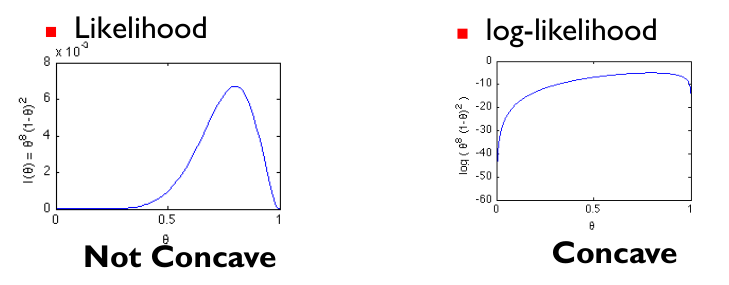
所謂的凹函式和凸函式，凹函式斜率逐漸減小，凸函式斜率逐漸增大。所以凹函式“容易”求解極大值（極值為0時），凸函式“容易”求解極小值（極值為0時）。

EM演算法

EM演算法（Expectation Maximization）是在含有隱變數（latent variable）的模型下計算最大似然的一種演算法。所謂隱變數，是指我們沒有辦法觀測到的變數。比如，有兩枚硬幣A、B，每一次隨機取一枚進行拋擲，我們只能觀測到硬幣的正面與反面，而不能觀測到每一次取的硬幣是否為A；則稱每一次的選擇拋擲硬幣為隱變數。

用Y表示觀測資料，Z表示隱變數；Y和Z連在一起稱為完全資料( complete-data )，觀測資料Y又稱為不完全資料(incomplete-data)。觀測資料的似然函式：

P(Y|θ)=∑zP(Z|θ)P(Y|Z,θ)$$P(Y|\theta )={\sum }_{z}P(Z|\theta )P(Y|Z,\theta )$$

求模型引數的極大似然估計：

θ^=argmaxθlogP(Y|θ)$$\hat{\theta }=argma{x}_{\theta }logP(Y|\theta )$$

因為含有隱變數，此問題無法求解。因此，Dempster等人提出EM演算法用於迭代求解近似解。

所以EM演算法是一種特殊情況下的最大似然求解方法。

EM演算法比較簡單，分為兩個步驟：

• E步（E-step），以當前引數
  θ(i)${\theta }^{(i)}$ 計算Z$Z$的期望值。因為期望值中不再包含未知的隱含變數Z，所以是可以計算的。

Q(θ,θ(i))=EZ[logP(Y,X|θ)|Y,θ(i)]$$Q(\theta ,{\theta }^{(i)})=E_Z[logP(Y,X|\theta )|Y,{\theta }^{(i)}]$$

• M步（M-step），求使Q(θ,θ(i))$Q(\theta ,{\theta }^{(i)})$極大化的θ$\theta$，確定第i+1$i+1$次迭代的引數的估計值θ(i+1)${\theta }^{(i+1)}$

θ(i+1)=argmaxθQ(θ,θ(i))$${\theta }^{(i+1)}=argma{x}_{\theta }Q(\theta ,{\theta }^{(i)})$$

如此迭代直至演算法收斂。

案例

如圖所示，有兩枚硬幣A、B，每一個實驗隨機取一枚拋擲10次，共5個實驗，我們可以觀測到每一次所取的硬幣，估計引數A、B為正面的概率θ=(θA,θB)$\theta =({\theta }_A,{\theta }_B)$ ，根據極大似然估計求解。

如果我們不能觀測到每一次所取的硬幣，只能用EM演算法估計模型引數，演算法流程如圖所示：

隱變數Z$Z$為每次實驗中選擇A或B的概率，並初始化A為正面的概率為0.6，B為正面的概率為0.5。實驗進行了5次。每次都要進行一遍EM操作。每次都要計算隱含變數。取A的概率，和取B的概率。然後更新代估引數θA${\theta }_A$（A為正面的概率）和