關聯分析的基本概念

關聯分析（Association Analysis）：在大規模資料集中尋找有趣的關係。

頻繁項集（Frequent Item Sets）：經常出現在一塊的物品的集合，即包含0個或者多個項的集合稱為項集。

支援度（Support）：資料集中包含該項集的記錄所佔的比例，是針對項集來說的。

置信度（Confidence）：出現某些物品時，另外一些物品必定出現的概率，針對規則而言。

關聯規則（Association Rules）：暗示兩個物品之間可能存在很強的關係。形如A->B的表示式，規則A->B的度量包括支援度和置信度

項集支援度：一個項集出現的次數與資料集所有事物數的百分比稱為項集的支援度

eg:support(A⇒B)=support_count(A∪B)/N$eg:support(A\Rightarrow B)=support\mathrm{\_}count(A\cup B)/N$

支援度反映了A和B同時出現的概率，關聯規則的支援度等於頻繁集的支援度。

項集置信度：包含A的資料集中包含B的百分比

eg:confidence(A⇒B)=support_count(A∪B)/support_count(A)$eg:confidence(A\Rightarrow B)=support\mathrm{\_}count(A\cup B)/support\mathrm{\_}count(A)$

置信度反映瞭如果交易中包含A，則交易包含B的概率。也可以稱為在A發生的條件下，發生B的概率，成為條件概率。

只有支援度和置信度(可信度)較高的關聯規則才是使用者感興趣的。

關聯分析步驟

1、發現頻繁項集，即計算所有可能組合數的支援度，找出不少於人為設定的最小支援度的集合。

2、發現關聯規則，即計算不小於人為設定的最小支援度的集合的置信度，找到不小於認為設定的最小置信度規則。

關聯分析的兩種關係：簡單關聯關係和序列關聯關係

簡單關聯關係：

簡單關聯關係可以從經典的購物中進行分析，購買麵包的顧客80%都會購買牛奶，由於麵包和牛奶是早餐搭配的必需品，二者搭配構成了早餐的組成部分，這就是一種簡單的關聯關係。

序列關聯關係：

當購買一款新手機後，就會考慮去購買手機膜等手機配件，這就是一種序列關係，不會先買手機膜再買手機的，先後關係是非常明顯的，這種關係是一種順序性的關係，也就是一種序列關聯關係。

關聯規則：規則就是一種衡量事物的標準，也就是一個演算法。

簡單關聯規則演算法

演算法思想基礎

如果某個項集是頻繁的，那麼它的所有子集也是頻繁的。更常用的是它的逆否命題，即如果一個項集是非頻繁的，那麼它的所有超集也是非頻繁的。

簡單關聯規則是無指導的學習方法，著重探索內部結構。簡單關聯規則也是使用最多的技術，主要演算法包括：Apriori、GRI、Carma，其中Apriori和Carma主要是如何提高關聯規則的分析效率，而GRI注重如何將單一概念層次的關聯推廣到更多概念層次的關聯，進而揭示事物內在結構。

簡單關聯規則的資料儲存形式：一種是交易資料格式，一種是表格資料格式。

序列關聯規則演算法

序列關聯規則的核心就是找到事物發展的前後關聯性，研究序列關聯可以來推測事物未來的發展情況，並根據預測的發展情況進行事物的分配和安排。

如何設定合理的支援度和置信度？

對於某條規則：（A=a）−>（B=b）$（A=a）->（B=b）$（support=30%,confident=60%）；其中support=30%表示在所有的資料記錄中，同時出現A=a和B=b的概率為30%；confident=60%表示在所有的資料記錄中，在出現A=a的情況下出現B=b的概率為60%，也就是條件概率。支援度揭示了A=a和B=b同時出現的概率，置信度揭示了當A=a出現時，B=b是否會一定出現的概率。

（1）如果支援度和置信度閉值設定的過高，雖然可以減少挖掘時間，但是容易造成一些隱含在資料中非頻繁特徵項被忽略掉，難以發現足夠有用的規則；

（2）如果支援度和置信度閉值設定的過低，又有可能產生過多的規則，甚至產生大量冗餘和無效的規則，同時由於演算法存在的固有問題，會導致高負荷的計算量，大大增加挖掘時間。

關聯分析的應用

(1)：購物籃分析，通過檢視那些商品經常在一起出售，可以幫助商店瞭解使用者的購物行為，這種從資料的海洋中抽取只是可以用於商品定價、市場促銷、存貨管理等環節

(2)：在Twitter源中發現一些公共詞。對於給定的搜尋詞，發現推文中頻繁出現的單詞集合

(3)：從新聞網站點選流中挖掘新聞流行趨勢，挖掘哪些新聞廣泛被使用者瀏覽到

(4)：搜尋引擎推薦，在使用者輸入查詢時推薦同時相關的查詢詞項

(5)：發現毒蘑菇的相似特徵。這裡只對包含某個特徵元素（有毒素）的項集感興趣，從中尋找毒蘑菇中的一些公共特徵，利用這些特徵來避免遲到哪些有毒的蘑菇

(6)：圖書館資訊的書籍推薦，對於學生的借書資訊，不同專業學生的借書情況，來挖掘不同學生的借書情況，進行數目的推薦。

(7)：校園網新聞通知資訊的推薦，在對校園網新聞通知資訊進行挖掘的過程中，分析不同部門，不同學院的新聞資訊的不同，在進行新聞資訊瀏覽的過程中進行新聞的推薦。

Apriori演算法

假設我們有一家經營著4種商品（商品0，商品1，商品2和商品3）的雜貨店，2圖顯示了所有商品之間所有的可能組合：

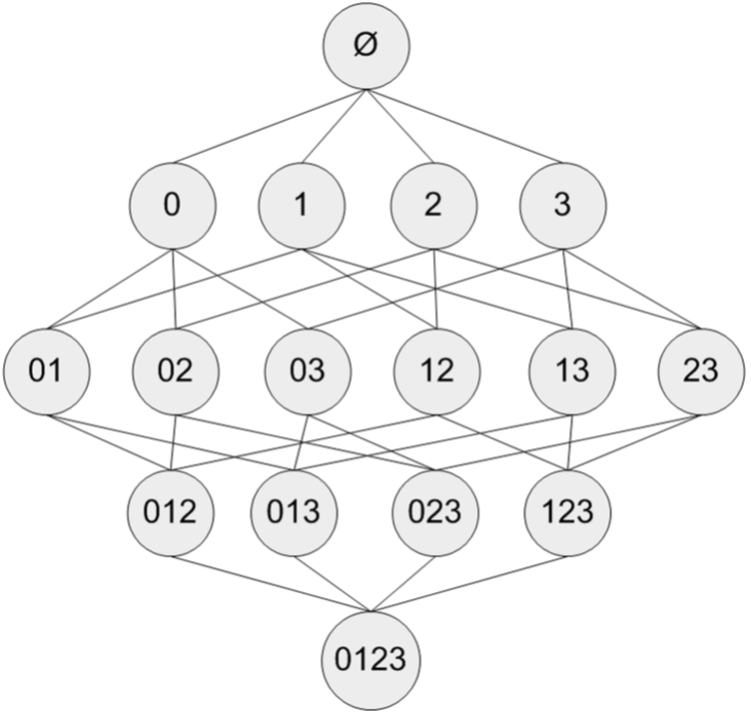
對於單個項集的支援度，我們可以通過遍歷每條記錄並檢查該記錄是否包含該項集來計算。對於包含N中物品的資料集共有2N−1$2^N-1$種項集組合，重複上述計算過程是不現實的。

研究人員發現一種所謂的Apriori原理，可以幫助我們減少計算量。Apriori原理是說如果某個項集是頻繁的，那麼它的所有子集也是頻繁的。

例如一個頻繁項集包含3個項A、B、C，則這三個項組成的子集{A},{B},{C},{A、B}，{A、C}、{B、C}一定是頻繁項集。

不過更常用的是它的逆否命題，即如果一個項集是非頻繁的，那麼它的所有超集也是非頻繁的。

在圖3中，已知陰影項集{2,3}是非頻繁的。利用這個知識，我們就知道項集{0,2,3}，{1,2,3}以及{0,1,2,3}也是非頻繁的。也就是說，一旦計算出了{2,3}的支援度，知道它是非頻繁的後，就可以緊接著排除{0,2,3}、{1,2,3}和{0,1,2,3}。

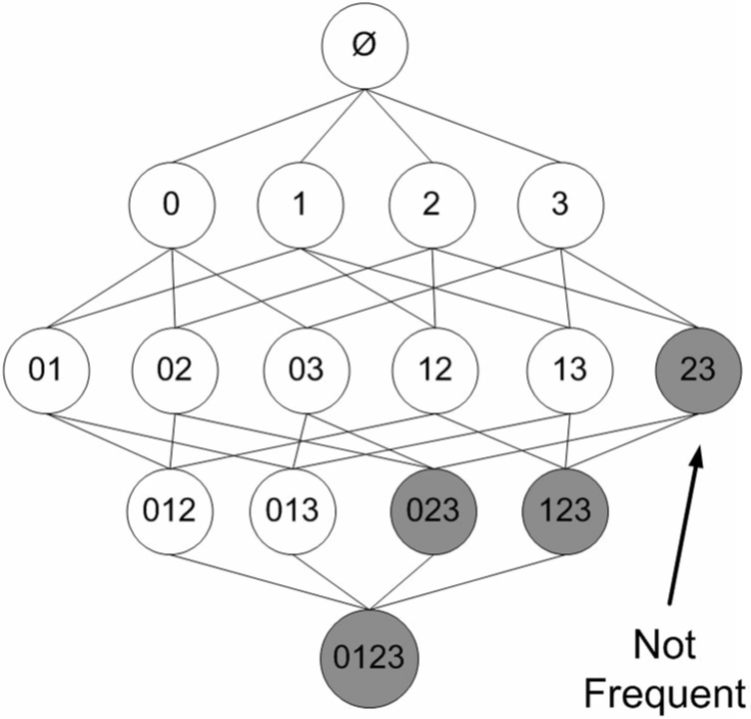
Apriori演算法是發現頻繁項集的一種方法。並不會找出關聯規則，關聯規則需要在找到頻繁項集以後我們再來統計。

Apriori演算法的兩個輸入引數分別是最小支援度和資料集。該演算法首先會生成所有單個元素的項集列表。接著掃描資料集來檢視哪些項集滿足最小支援度要求，那些不滿足最小支援度的集合會被去掉。然後，對剩下來的集合進行組合以生成包含兩個元素的項集。接下來，再重新掃描交易記錄，去掉不滿足最小支援度的項集。該過程重複進行直到所有項集都被去掉。

該演算法需要不斷尋找候選集，然後剪枝即去掉非頻繁子集的候選集，時間複雜度由暴力列舉所有子集的指數級別O（n2）$O（n^2）$降為多項式級別，多項式具體系數視底層實現情況而定的。

Ariori演算法有兩個主要步驟：

1、連線：（將項集進行兩兩連線形成新的候選集）

利用已經找到的k$k$個項的頻繁項集Lk$L_k$，通過兩兩連線得出候選集Ck+1$C_{k+1}$，注意進行連線的Lk[i]$L_k[i]$，Lk[j]$L_k[j]$，必須有k−1個$k-1個$屬性值相同，然後另外兩個不同的分別分佈在Lk[i]$L_k[i]$，Lk[j]$L_k[j]$中，這樣的求出的Ck+1$C_{k+1}$為Lk+1$L_{k+1}$的候選集。

2、剪枝：（去掉非頻繁項集）

候選集 Ck+1$C_{k+1}$中的並不都是頻繁項集，必須剪枝去掉，越早越好以防止所處理的資料無效項越來越多。只有當子集都是頻繁集的候選集才是頻繁集，這是剪枝的依據。

演算法實現

from numpy import *


def loadDataSet():
    return [[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]]

# 獲取候選1項集，dataSet為事務集。返回一個list，每個元素都是set集合
def createC1(dataSet):
    C1 = []   # 元素個數為1的項集（非頻繁項集，因為還沒有同最小支援度比較）
    for transaction in dataSet:
        for item in transaction:
            if not [item] in C1:
                C1.append([item])
    C1.sort()  # 這裡排序是為了，生成新的候選集時可以直接認為兩個n項候選集前面的部分相同
    # 因為除了候選1項集外其他的候選n項集都是以二維列表的形式存在，所以要將候選1項集的每一個元素都轉化為一個單獨的集合。
    return list(map(frozenset, C1))   #map(frozenset, C1)的語義是將C1由Python列表轉換為不變集合（frozenset，Python中的資料結構）




# 找出候選集中的頻繁項集
# dataSet為全部資料集，Ck為大小為k（包含k個元素）的候選項集，minSupport為設定的最小支援度
def scanD(dataSet, Ck, minSupport):
    ssCnt = {}   # 記錄每個候選項的個數
    for tid in dataSet:
        for can in Ck:
            if can.issubset(tid):
                ssCnt[can] = ssCnt.get(can, 0) + 1   # 計算每一個項集出現的頻率
    numItems = float(len(dataSet))
    retList = []
    supportData = {}
    for key in ssCnt:
        support = ssCnt[key] / numItems
        if support >= minSupport:
            retList.insert(0, key)  #將頻繁項集插入返回列表的首部
        supportData[key] = support
    return retList, supportData   #retList為在Ck中找出的頻繁項集（支援度大於minSupport的），supportData記錄各頻繁項集的支援度


# 通過頻繁項集列表Lk和項集個數k生成候選項集C(k+1)。
def aprioriGen(Lk, k):
    retList = []
    lenLk = len(Lk)
    for i in range(lenLk):
        for j in range(i + 1, lenLk):
            # 前k-1項相同時，才將兩個集合合併，合併後才能生成k+1項
            L1 = list(Lk[i])[:k-2]; L2 = list(Lk[j])[:k-2]   # 取出兩個集合的前k-1個元素
            L1.sort(); L2.sort()
            if L1 == L2:
                retList.append(Lk[i] | Lk[j])
    return retList

# 獲取事務集中的所有的頻繁項集
# Ck表示項數為k的候選項集，最初的C1通過createC1()函式生成。Lk表示項數為k的頻繁項集，supK為其支援度，Lk和supK由scanD()函式通過Ck計算而來。
def apriori(dataSet, minSupport=0.5):
    C1 = createC1(dataSet)  # 從事務集中獲取候選1項集
    D = list(map(set, dataSet))  # 將事務集的每個元素轉化為集合
    L1, supportData = scanD(D, C1, minSupport)  # 獲取頻繁1項集和對應的支援度
    L = [L1]  # L用來儲存所有的頻繁項集
    k = 2
    while (len(L[k-2]) > 0): # 一直迭代到項集數目過大而在事務集中不存在這種n項集
        Ck = aprioriGen(L[k-2], k)   # 根據頻繁項集生成新的候選項集。Ck表示項數為k的候選項集
        Lk, supK = scanD(D, Ck, minSupport)  # Lk表示項數為k的頻繁項集，supK為其支援度
        L.append(Lk);supportData.update(supK)  # 新增新頻繁項集和他們的支援度
        k += 1
    return L, supportData



if __name__=='__main__':
    dataSet = loadDataSet()  # 獲取事務集。每個元素都是列表
    # C1 = createC1(dataSet)  # 獲取候選1項集。每個元素都是集合
    # D = list(map(set, dataSet))  # 轉化事務集的形式，每個元素都轉化為集合。
    # L1, suppDat = scanD(D, C1, 0.5)
    # print(L1,suppDat)


    L, suppData = apriori(dataSet,minSupport=0.7)
    print(L,suppData)

FP-growth演算法來高效發現頻繁項集

FP樹：用於編碼資料集的有效方式

FP-growth演算法將資料儲存在一種稱為FP樹的緊湊資料結構中。FP代表頻繁模式（Frequent Pattern）。一棵FP樹看上去與電腦科學中的其他樹結構類似，但是它通過連結（link）來連線相似元素，被連起來的元素項可以看成一個連結串列。

與搜尋樹不同的是，一個元素項可以在一棵FP樹種出現多次。FP樹會儲存項集的出現頻率，而每個項集會以路徑的方式儲存在數中。 樹節點上給出集合中的單個元素及其在序列中的出現次數，路徑會給出該序列的出現次數。

相似項之間的連結稱為節點連結（node link），用於快速發現相似項的位置。

下圖給出了FP樹的一個例子。

事務集

事務ID	事務中的元素項
001	r, z, h, j, p
002	z, y, x, w, v, u, t, s
003	z
004	r, x, n, o, s
005	y, r, x, z, q, t, p
006	y, z, x, e, q, s, t, m

生成的FP樹為

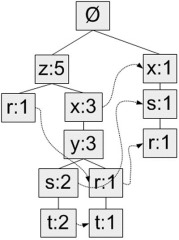
對FP樹的解讀：

圖中，元素項z出現了5次，集合{r, z}出現了1次。於是可以得出結論：z一定是自己本身或者和其他符號一起出現了4次。集合{t, s, y, x, z}出現了2次，集合{t, r, y, x, z}出現了1次，z本身單獨出現1次。就像這樣，FP樹的解讀方式是讀取某個節點開始到根節點的路徑。路徑上的元素構成一個頻繁項集，開始節點的值表示這個項集的支援度。根據圖5，我們可以快速讀出項集{z}的支援度為5、項集{t, s, y, x, z}的支援度為2、項集{r, y, x, z}的支援度為1、項集{r, s, x}的支援度為1。FP樹中會多次出現相同的元素項，也是因為同一個元素項會存在於多條路徑，構成多個頻繁項集。但是頻繁項集的共享路徑是會合並的，如圖中的{t, s, y, x, z}和{t, r, y, x, z}

和之前一樣，我們取一個最小閾值，出現次數低於最小閾值的元素項將被直接忽略。圖中將最小支援度設為3，所以q和p沒有在FP中出現。

FP-growth演算法的工作流程如下。首先構建FP樹，然後利用它來挖掘頻繁項集。為構建FP樹，需要對原始資料集掃描兩遍。第一遍對所有元素項的出現次數進行計數。資料庫的第一遍掃描用來統計出現的頻率，而第二遍掃描中只考慮那些頻繁元素。

FP-growth演算法發現頻繁項集的基本過程如下：

• 構建FP樹
• 從FP樹中挖掘頻繁項集

頭指標表

FP-growth演算法還需要一個稱為頭指標表的資料結構，其實很簡單，就是用來記錄各個元素項的總出現次數的陣列，再附帶一個指標指向FP樹中該元素項的第一個節點。這樣每個元素項都構成一條單鏈表。圖示說明：

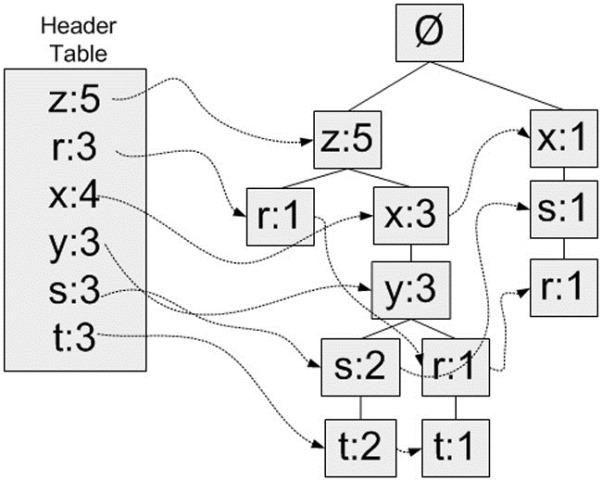
這裡使用Python字典作為資料結構，來儲存頭指標表。以元素項名稱為鍵，儲存出現的總次數和一個指向第一個相似元素項的指標。

第一次遍歷資料集會獲得每個元素項的出現頻率，去掉不滿足最小支援度的元素項，生成這個頭指標表。

元素項排序

上文提到過，FP樹會合並相同的頻繁項集（或相同的部分）。因此為判斷兩個項集的相似程度需要對項集中的元素進行排序（不過原因也不僅如此，還有其它好處）。排序基於元素項的絕對出現頻率（總的出現次數）來進行。在第二次遍歷資料集時，會讀入每個項集（讀取），去掉不滿足最小支援度的元素項（過濾），然後對元素進行排序（重排序）。

構建FP樹

在對事務記錄過濾和排序之後，就可以構建FP樹了。從空集開始，將過濾和重排序後的頻繁項集一次新增到樹中。如果樹中已存在現有元素，則增加現有元素的值；如果現有元素不存在，則向樹新增一個分支。對前兩條事務進行新增的過程：

實現流程

輸入：資料集、最小值尺度
輸出：FP樹、頭指標表

• 1、遍歷資料集，統計各元素項出現次數，建立頭指標表
• 2、移除頭指標表中不滿足最小值尺度的元素項
• 3、第二次遍歷資料集，建立FP樹。對每個資料集中的項集：
  
  • 3.1 初始化空FP樹
  • 3.2 對每個項集進行過濾和重排序
  • 3.3 使用這個項集更新FP樹，從FP樹的根節點開始：
    
    • 3.3.1 如果當前項集的第一個元素項存在於FP樹當前節點的子節點中，則更新這個子節點的計數值
    • 3.3.2 否則，建立新的子節點，更新頭指標表
    • 3.3.3 對當前項集的其餘元素項和當前元素項的對應子節點遞迴3.3的過程

從一棵FP樹種挖掘頻繁項集

從FP樹中抽取頻繁項集的三個基本步驟如下：

• 從FP樹中獲得條件模式基；
• 利用條件模式基，構建一個條件FP樹；
• 迭代重複步驟1步驟2，直到樹包含一個元素項為止。

其中“條件模式基”是以所查詢元素項為結尾的路徑集合。每一條路徑其實都是一條字首路徑（prefix path）。簡而言之，一條字首路徑是介於所查詢元素項與樹根節點之間的所有內容。
例如

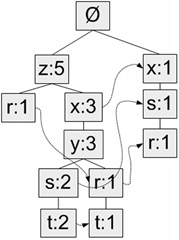
則每一個頻繁元素項的條件模式基為：

頻繁項	字首路徑
z	{}: 5
r	{x, s}: 1, {z, x, y}: 1, {z}: 1
x	{z}: 3, {}: 1
y	{z, x}: 3
s	{z, x, y}: 2, {x}: 1
t	{z, x, y, s}: 2, {z, x, y, r}: 1

發現規律了嗎，z存在於路徑{z}中，因此字首路徑為空，另新增一項該路徑中z節點的計數值5構成其條件模式基；r存在於路徑{r, z}、{r, y, x, z}、{r, s, x}中，分別獲得字首路徑{z}、{y, x, z}、{s, x}，另新增對應路徑中r節點的計數值（均為1）構成r的條件模式基；以此類推。

建立條件FP樹

對於每一個頻繁項，都要建立一棵條件FP樹。可以使用剛才發現的條件模式基作為輸入資料，並通過相同的建樹程式碼來構建這些樹。例如，對於r，即以“{x, s}: 1, {z, x, y}: 1, {z}: 1”為輸入，呼叫函式createTree()獲得r的條件FP樹；對於t，輸入是對應的條件模式基“{z, x, y, s}: 2, {z, x, y, r}: 1”。

遞迴查詢頻繁項集

有了FP樹和條件FP樹，我們就可以在前兩步的基礎上遞迴得查詢頻繁項集。

遞迴的過程是這樣的：
輸入：我們有當前資料集的FP樹（inTree，headerTable）

• 1、初始化一個空列表preFix表示字首
• 2、初始化一個空列表freqItemList接收生成的頻繁項集（作為輸出）
• 3、對headerTable中的每個元素basePat（按計數值由小到大），遞迴：
  
  • 3.1 記basePat + preFix為當前頻繁項集newFreqSet
  • 3.2 將newFreqSet新增到freqItemList中
  • 3.3 計算t的條件FP樹（myCondTree、myHead）
  • 3.4 當條件FP樹不為空時，繼續下一步；否則退出遞迴
  • 3.5 以myCondTree、myHead為新的輸入，以newFreqSet為新的preFix，外加freqItemList，遞迴這個過程

實現程式碼

# FP樹類
class treeNode:
    def __init__(self, nameValue, numOccur, parentNode):
        self.name = nameValue  #節點元素名稱，在構造時初始化為給定值
        self.count = numOccur   # 出現次數，在構造時初始化為給定值
        self.nodeLink = None   # 指向下一個相似節點的指標，預設為None
        self.parent = parentNode   # 指向父節點的指標，在構造時初始化為給定值
        self.children = {}  # 指向子節點的字典，以子節點的元素名稱為鍵，指向子節點的指標為值，初始化為空字典

    # 增加節點的出現次數值
    
            
  
           

              
              
            
            
相關推薦
			   
            
            
            
 

    

    
    
python機器學習案例系列教程——關聯分析（Apriori、FP-growth）
     
 
							
							
							



關聯分析的基本概念

關聯分析（Association Analysis）：在大規模資料集中尋找有趣的關係。

頻繁項集（Frequent Item Sets）：經常出現在一塊的物品的集合，即包含0個或者多個項的集合稱為項集。

支援度（Support） 

  
 

    

    
    
python機器學習案例系列教程——決策樹（ID3、C4.5、CART）
     
 
							
							
							



決策樹簡介

決策樹算是最好理解的分類器了。決策樹就是一個多層if-else函式，就是對物件屬性進行多層if-else判斷，獲取目標屬性（類標籤）的類別。由於只使用if-else對特徵屬性進行判斷，所以一般特徵屬性為離散值，即使為連續值也會先進行區間離散 

  
 

    

    
    
python機器學習案例系列教程——k均值聚類、k中心點聚類
     
 
							
							
							

上一篇我們學習了層次聚類。層次聚類只是迭代的把最相近的兩個聚類匹配起來。並沒有給出能給出多少的分組。今天我們來研究一個K均值聚類。就是給定分組數目的基礎上再來聚類。即將所有的樣本資料集分成K個組，每個組內儘可能相似，每個組間又儘可能不相似。

k均值聚類和k 

  
 

    

    
    
python機器學習案例系列教程——極大似然估計、EM演算法
     
 
							
							
							



極大似然

極大似然（Maximum Likelihood）估計為用於已知模型的引數估計的統計學方法。

也就是求使得似然函式最大的代估引數的值。而似然函式就是如果引數已知則已出現樣本出現的概率。

比如，我們想了解拋硬幣是正面（head）的概率分佈θθ 

  
 

    

    
    
關聯分析（Apriori，FP-growth）
     
 
                關聯分析是資料探勘中的重要組成部分，旨在挖掘資料中的頻繁模式。我們可以通過一個案例資料庫挖掘著名案例來大致瞭解挖掘頻繁項集併產生關聯規則。

關聯分析的基本概念

關聯分析：在大規模資料集中尋找有趣的關係

頻繁項集：經常出現在一起的物品集合，即包含0個或者多個項的集合

關 

  
 

    

    
    
python機器學習案例系列教程——聚類演算法總結
     
 
							
							
							
  全棧工程師開發手冊 （作者：欒鵬）
  
  




一、什麼是聚類？

聚類（Clustering）：聚類是一個人們日常生活的常見行為，即所謂“物以類聚，人以群分”，核心的思想也就是聚類。人們總是不斷地改進下意識中的聚類模式來學習如何區分各個事物和人。 

  
 

    

    
    
python機器學習案例系列教程——最小生成樹（MST）的Prim演算法和Kruskal演算法
     
 
							
							
							



最小生成樹MST

一個有 n 個結點的連通圖的生成樹是原圖的極小連通子圖，且包含原圖中的所有 n 個結點，並且有保持圖連通的最少的邊。

也就是說，用原圖中有的邊，連線n個節點，保證每個節點都被連線，且使用的邊的數目最少。

最小權重生成樹

在一給定 

  
 

    

    
    
python機器學習案例系列教程——整合學習（Bagging、Boosting、隨機森林RF、AdaBoost、GBDT、xgboost）
     
 
							
							
							

可以通過聚集多個分類器的預測結果提高分類器的分類準確率，這一方法稱為整合（Ensemble）學習或分類器組合（Classifier Combination），該方法由訓練資料構建一組基分類器（Base Classifier），然後通過對每個基分類器的預測進行 

  
 

    

    
    
python機器學習案例系列教程——CTR/CVR中的FM、FFM演算法
     
 
							
							
							
  全棧工程師開發手冊 （作者：欒鵬）
  
  




FM問題來源

CTR/CVR預測時，使用者的性別、職業、教育水平、品類偏好，商品的品類等，經過One-Hot編碼轉換後都會導致樣本資料的稀疏性。特別是商品品類這種型別的特徵，如商品的末級品類約有55 

  
 

    

    
    
Python機器學習筆記：線性判別分析（LDA）演算法
     
 預備知識
　　首先學習兩個概念：
　　線性分類：指存在一個線性方程可以把待分類資料分開，或者說用一個超平面能將正負樣本區分開，表示式為y=wx，這裡先說一下超平面，對於二維的情況，可以理解為一條直線，如一次函式。它的分類演算法是基於一個線性的預測函式，決策的邊界是平的，比如直線和平面。一般的方法有感知器，最小 

  
 

    

    
    
python機器學習----利用sklearn進行情感分析
     
 
							
							
							import jieba
from collections import defaultdict
import os
from sklearn.feature_extraction.text import TfidfTransformer
from sklear 

  
 

    

    
    
python機器學習入門到精通--實戰分析(三)
     
 
							
							
							利用sklearn分析鳶尾花

前面兩篇文章提到了機器學習的入門的幾個基礎庫及拓展練習，現在我們就對前面知識點進行彙總進行一個簡單的機器學習應用，並構建模型。 
練習即假定一名植物專家收集了每一朵鳶尾花的測量資料：花瓣的長度和寬度以及花萼的長度和寬度，所有測量結 

  
 

    

    
    
Python機器學習實戰專案--預測紅酒質量（超詳細）
     
  
 
 用Scikit-Learn（sklearn）建立模型
 1 環境搭建
  Python 3+NumPy+Pandas+Scikit-Learn (sklearn)
 2 匯入庫和模組
 Numpy是比Python自身的巢狀列表（nested list structure)結構要高效的多的一 

  
 

    

    
    
python機器學習：：資料預處理（1）【轉】
     
 
                轉載自：http://2hwp.com/2016/02/03/data-preprocessing/

常見的資料預處理方法，以下通過sklearn的preprocessing模組來介紹;

1. 標準化（Standardization or Mean Removal and 

  
 

    

    
    
Python機器學習及實踐——基礎篇11（迴歸樹）
     
 
                迴歸樹在選擇不同特徵作為分裂節點的策略上，與基礎篇6的決策樹的思路類似。不同之處在於，迴歸樹葉節點的資料型別不是離散型，而是連續型。決策樹每個葉節點依照訓練資料表現的概率傾向決定了其最終的預測類；而回歸樹的葉節點確實一個個具體的值，從預測值連續這個意義上嚴格地講，迴歸樹不能成 

  
 

    

    
    
Python機器學習及實踐——基礎篇7（分類整合模型）
     
 
                    常言道：“一個籬笆三個樁，一個好漢三個幫”。整合分類模型便是綜合考量多個分類器的預測結果，從而做出決策。只是這種“綜合考量”的方式大體上分為兩種：    一種是利用相同的訓練資料同時搭建多個獨立的分類模型，然後通過投票的方式，以少數服從多數的原則作出最終的分類決策。比 

  
 

    

    
    
Python機器學習及實踐——基礎篇10（K近鄰迴歸）
     
 
                    在基礎篇5中提到裡這類模型不需要訓練引數的特點。在迴歸任務重，k近鄰（迴歸）模型同樣只是藉助周圍K個最近訓練樣本的目標數值，對待測樣本的迴歸值進行決策。自然，也衍生出衡量待測樣吧迴歸值的不同方式，即到底是對K個近鄰目標數值使用普通的算術平均演算法，還是同時考慮距離的差 

  
 

    

    
    
Python機器學習筆記：奇異值分解（SVD）演算法
     
 完整程式碼及其資料，請移步小編的GitHub
　　傳送門：請點選我
　　如果點選有誤：https://github.com/LeBron-Jian/MachineLearningNote
　　奇異值分解（Singular  Value Decomposition，後面簡稱 SVD）是線上性代數中一種 

  
 

    

    
    
吳恩達機器學習第5周Neural Networks（Cost Function and Backpropagation）
     
 and   div   bsp   關於   邏輯回歸   info   src   clas   分享   5.1 Cost Function
假設訓練樣本為：{(x1),y(1)),(x(2),y(2)),...(x(m),y(m))}
L  = total no.of layers in network 

  
 

    

    
    
關聯規則演算法Apriori以及FP-growth學習
     
 關聯規則演算法Apriori以及FP-growth學習 
　　最近選擇了關聯規則演算法進行學習，目標是先學習Apriori演算法，再轉FP-growth演算法，因為Spark-mllib庫支援的關聯演算法是FP，隨筆用於邊學邊記錄，完成後再進行整理 
一、概述 
　　關聯規則是一種常見的推薦演算法，用於從發現