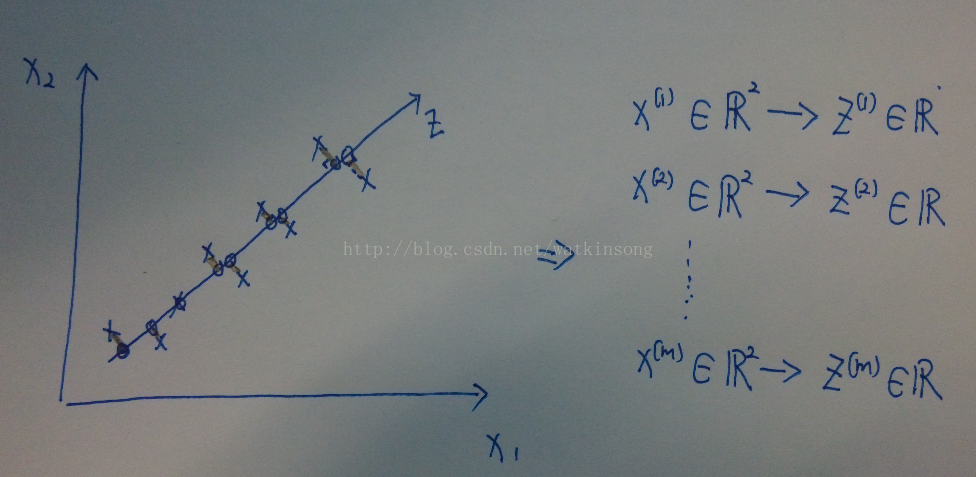PCA（主成分分析）降維演算法詳解和程式碼

阿新 • • 發佈：2019-02-03

1. 前言

PCA ： principal component analysis ( 主成分分析)

最近發現我的一篇關於PCA演算法總結以及個人理解的部落格的訪問量比較高，剛好目前又重新學習了一下PCA （主成分分析）降維演算法，所以打算把目前掌握的做個全面的整理總結，能夠對有需要的人有幫助。自己再看自己寫的那個關於PCA的部落格，發現還是比較混亂的，希望這裡能過做好整理。本文的所有總結參考了Andrew Ng的PCA教程，有興趣的可以自己學習。

上一篇關於PCA 的部落格： http://blog.csdn.net/watkinsong/article/details/8234766

，在這篇部落格中，有關於我最初在讀研的時候關於PCA的認識，但是不是很系統，然後裡面卻給出了很多我總結的網路上的資料，以及根據我個人使用的經驗總結的感悟，所以還是收到了很多的好評， o(∩∩)o...哈哈，謝謝各位的支援。

@copyright by watkins.song ^_^

2. PCA的應用範圍

PCA的應用範圍有：

1. 資料壓縮

1.1 資料壓縮或者資料降維首先能夠減少記憶體或者硬碟的使用，如果記憶體不足或者計算的時候出現記憶體溢位等問題，就需要使用PCA獲取低維度的樣本特徵。

1.2 其次，資料降維能夠加快機器學習的速度。

2. 資料視覺化

在很多情況下，可能我們需要檢視樣本特徵，但是高維度的特徵根本無法觀察，這個時候我們可以將樣本的特徵降維到2D或者3D，也就是將樣本的特徵維數降到2個特徵或者3個特徵，這樣我們就可以採用視覺化觀察資料。

3. PCA原理簡介

3.1 基礎入門

這裡我只給出在需要使用PCA的時候需要了解的最基本的PCA的原理，瞭解這些原理後對於正常的使用沒有問題，如果想要深入瞭解PCA，需要學習一些矩陣分析的知識，更加詳細的PCA演算法請見wikipedia。

首先，我們定義樣本和特徵，假定有 m 個樣本，每個樣本有 n 個特徵，可以如下表示：

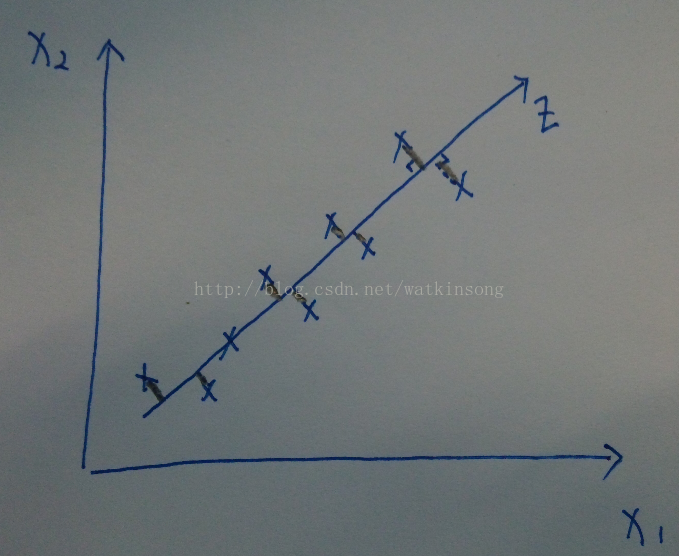
由簡到難，先看一下從2D 降維到1D的比較直觀的表示：

在上圖中，假設只有兩個特徵x1, x2, 然後需要降維到1D，這個時候我們可以觀察途中X所表示的樣本點基本上分佈在一條直線上，那麼就可以將所有的用(x1, x2)平面表示的座標對映到影象畫出的直線z上，上圖中的黑色鉛筆線表示樣本點對映的過程。

對映到直線Z後，如果只用直線Z表示樣本的空間分佈，就可以用1個座標表示每個樣本了，這樣就將2D的特徵降維到1D的特徵。同樣的道理，如果將3D的特徵降維到2D，就是將具有3D特徵的樣本從一個三維空間中對映到二維空間。

在上圖中，將所有的二維特徵的樣本點對映到了一維直線上，這樣，從上圖中可以看出在對映的過程中存在對映誤差。

在上圖中，用圓圈表示了樣本對映後的座標位置。這些位置可以叫做近似位置，以後還要用到這些位置計算對映誤差。

因為在降維對映的過程中，存在對映誤差，所有在對高維特徵降維之前，需要做特徵歸一化（feature normalization）, 這個歸一化操作包括：（1） feature scaling (讓所有的特徵擁有相似的尺度，要不然一個特徵特別小，一個特徵特別大會影響降維的效果) （2） zero mean normalization (零均值歸一化)。

在上圖中，也可以把降維的過程看作找到一個或者多個向量u1, u2, ...., un，使得這些向量構成一個新的向量空間（需要學習矩陣分析哦），然後把需要降維的樣本對映到這個新的樣本空間上。

對於2D -> 1D 的降維過程，可以理解為找到一個向量u1, u1表示了一個方向，然後將所有的樣本對映到這個方向上，其實，一個向量也可以表示一個樣本空間。

對於3D -> 2D 的降維過程，可以理解為找到兩個向量u1, u2, (u1, u2) 這兩個向量定義了一個新的特徵空間，然後將原樣本空間的樣本對映到新的樣本空間。

對於n-D -> k-D 的降維過程，可以理解為找到 k 個向量 u1, u2, ..., uk, 這k個向量定義了新的向量空間，然後進行樣本對映。

3.2 Cost Function

既然樣本對映存在誤差，就需要計算每次對映的誤差大小。採用以下公式計算誤差大小：

X-approx表示的是樣本對映以後的新的座標，這個座標如果位置如果用當前的樣本空間表示，維度和樣本X是一致的。

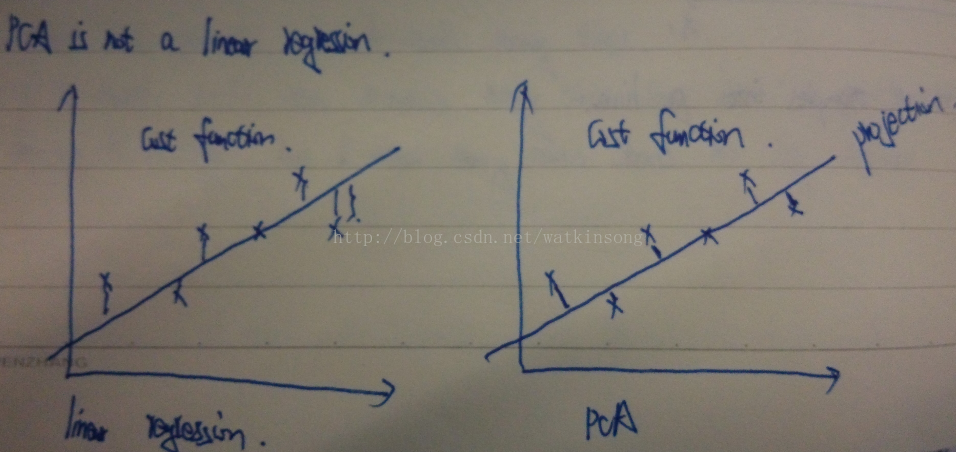
要特別注意， PCA降維和linear regression是不一樣的，雖然看上去很一致，但是linear regression的cost function的計算是樣本上線垂直的到擬合線的距離，而PCA的cost function 是樣本點到擬合線的垂直距離。差別如下圖所示：

3.3 PCA 計算過程

（A） Feature Normalization

首先要對訓練樣本的特徵進行歸一化，特別強調的是，歸一化操作只能在訓練樣本中進行，不能才CV集合或者測試集合中進行，也就是說歸一化操作計算的各個引數只能由訓練樣本得到，然後測試樣本根據這裡得到的引數進行歸一化，而不能直接和訓練樣本放在一起進行歸一化。另外，在訓練PCA降維矩陣的過程中，也不能使用CV樣本或者測試樣本，這樣做是不對的。有很多人在使用PCA訓練降維矩陣的時候，直接使用所有的樣本進行訓練，這樣實際上相當於作弊的，這樣的話降維矩陣是在包含訓練樣本和測試樣本以及CV樣本的情況下訓練得到的，在進行測試的時候，測試樣本會存在很大的優越性，因為它已經知道了要降維到的空間情況。特徵歸一化直接給出程式碼參考：

function [X_norm, mu, sigma] = featureNormalize(X)
%FEATURENORMALIZE Normalizes the features in X
% FEATURENORMALIZE(X) returns a normalized version of X where
% the mean value of each feature is 0 and the standard deviation
% is 1. This is often a good preprocessing step to do when
% working with learning algorithms.
mu = mean(X);
X_norm = bsxfun(@minus, X, mu);
sigma = std(X_norm);
X_norm = bsxfun(@rdivide, X_norm, sigma);
% ============================================================
end

注意：這裡的X是一個m * n 的矩陣，有 m 個樣本，每個樣本包含 n 個特徵，每一行表示一個樣本。 X_norm是最終得到的特徵，首先計算了所有訓練樣本每個特徵的均值，然後減去均值，然後除以標準差。

（B）計算降維矩陣

B1. 首先計算樣本特徵的協方差矩陣如下圖所示，如果是每個樣本單獨計算，則採用圖中橫線上的公式，如果是採用矩陣化的計算，則採用橫線下的公式。

B2. 計算協方差矩陣的特徵值和特徵向量
採用奇異值分解的演算法計算協方差矩陣的特徵值和特徵向量，奇異值分解是個比較複雜的概念，如果有興趣可以檢視wikipedia，也可以直接使用matlab或者octave已經提供的奇異值分解的介面。

在上圖中， U 則是計算得到的協方差矩陣的所有特徵向量，每一列都是一個特徵向量，並且特徵向量是根據特徵大小由大到小進行排序的， U 的維度為 n * n 。 U 也被稱為降維矩陣。利用U 可以將樣本進行降維。預設的U 是包含協方差矩陣的所有特徵向量，如果想要將樣本降維到 k 維，那麼就可以選取 U 的前 k 列， Uk 則可以用來對樣本降維到 k 維。這樣 Uk 的維度為 n * k

（C）降維計算

獲得降維矩陣後，即可通過降維矩陣將樣本對映到低維空間上。降維公式如下圖所示：

如果是對於矩陣X 進行降維， X 是 m * n的，那麼降維後就變為 m * k 的維度，每一行表示一個樣本的特徵。 k 越大，也就是使用的U 中的特徵向量越多，那麼導致的降維誤差越小，也就是更多的保留的原來的特徵的特性。反之亦然。從資訊理論的角度來看，如果選擇的 k 越大，也就是系統的熵越大，那麼就可以認為保留的原來樣本特徵的不確定性也就越大，就更加接近真實的樣本資料。如果 k 比較小，那麼系統的熵較小，保留的原來的樣本特徵的不確定性就越少，導致降維後的資料不夠真實。（完全是我個人的觀點）關於 k 的選擇，可以參考如下公式：

上面這個公式要求 <= 0.01，也就是說保留了系統的99%的不確定性。需要計算的就是，找到一個最小的 k 使得上面的公式成立，但是如果計算上面公式，計算量太大，並且對於每一個 k 取值都需要重新計算降維矩陣。可以採用下面的公式計算 k 的取值，因為在對協方差矩陣進行奇異值分解的時候返回了 S , S 為協方差矩陣的特徵值，並且 S 是對角矩陣，維度為 n * n，計算 k 的取值如下：

3.5 重構（reconstruction，根據降維後資料重構原資料），資料還原

獲得降維後的資料，可以根據降維後的資料還原原始資料。還原原始資料的過程也就是獲得樣本點對映以後在原空間中的估計位置的過程，即計算 X-approx的過程。

使用降維用的降維矩陣 Uk，然後將降維後的樣本 z 還原回原始特徵，就可以用上圖所示的公式。

4. PCA的應用示例

貌似本頁已經寫的太多了，所以這裡示例另外給出。由於篇幅問題，這裡只給出程式碼，關於程式碼的解釋和插圖，請訪問上面連結

%% Initialization
clear ; close all; clc
fprintf('this code will load 12 images and do PCA for each face.\n');
fprintf('10 images are used to train PCA and the other 2 images are used to test PCA.\n');
m = 4000; % number of samples
trainset = zeros(m, 32 * 32); % image size is : 32 * 32
for i = 1 : m
img = imread(strcat('./img/', int2str(i), '.bmp'));
img = double(img);
trainset(i, :) = img(:);
end
%% before training PCA, do feature normalization
mu = mean(trainset);
trainset_norm = bsxfun(@minus, trainset, mu);
sigma = std(trainset_norm);
trainset_norm = bsxfun(@rdivide, trainset_norm, sigma);
%% we could save the mean face mu to take a look the mean face
imwrite(uint8(reshape(mu, 32, 32)), 'meanface.bmp');
fprintf('mean face saved. paused\n');
pause;
%% compute reduce matrix
X = trainset_norm; % just for convience
[m, n] = size(X);
U = zeros(n);
S = zeros(n);
Cov = 1 / m * X' * X;
[U, S, V] = svd(Cov);
fprintf('compute cov done.\n');
%% save eigen face
for i = 1:10
ef = U(:, i)';
img = ef;
minVal = min(img);
img = img - minVal;
max_val = max(abs(img));
img = img / max_val;
img = reshape(img, 32, 32);
imwrite(img, strcat('eigenface', int2str(i), '.bmp'));
end
fprintf('eigen face saved, paused.\n');
pause;
%% dimension reduction
k = 100; % reduce to 100 dimension
test = zeros(10, 32 * 32);
for i = 4001:4010
img = imread(strcat('./img/', int2str(i), '.bmp'));
img = double(img);
test(i - 4000, :) = img(:);
end
% test set need to do normalization
test = bsxfun(@minus, test, mu);
% reduction
Uk = U(:, 1:k);
Z = test * Uk;
fprintf('reduce done.\n');
%% reconstruction
%% for the test set images, we only minus the mean face,
% so in the reconstruct process, we need add the mean face back
Xp = Z * Uk';
% show reconstructed face
for i = 1:5
face = Xp(i, :) + mu;
face = reshape((face), 32, 32);
imwrite(uint8(face), strcat('./reconstruct/', int2str(4000 + i), '.bmp'));
end
%% for the train set reconstruction, we minus the mean face and divide by standard deviation during the train
% so in the reconstruction process, we need to multiby standard deviation first,
% and then add the mean face back
trainset_re = trainset_norm * Uk; % reduction
trainset_re = trainset_re * Uk'; % reconstruction
for i = 1:5
train = trainset_re(i, :);
train = train .* sigma;
train = train + mu;
train = reshape(train, 32, 32);
imwrite(uint8(train), strcat('./reconstruct/', int2str(i), 'train.bmp'));
end
fprintf('job done.\n');

轉自：http://blog.csdn.net/watkinsong/article/details/38536463