運用PCA(主成分分析法)進行人臉識別的MATLAB 程式碼實現
PCA(主成分分析演算法)出現的比較早。
PCA演算法依賴於一個基本假設:一類影象具有某些相似的特徵(如人臉),在整個影象空間中呈現出聚類性,因而形成一個子空間,即所謂特徵子空間,PCA變換是最佳正交變換,利用變換基的線性組合可以描述、表達和逼近這一類影象,因此可以進行影象識別,PCA包含訓練和識別兩個階段。
訓練階段:
1)計算平均臉
2)計算差值臉
3)構建協方差矩陣
4)計算矩陣的特徵值和特徵向量
5)將每幅人臉的差值臉投影到特徵空間W上,就可以得到每幅人臉的P的特徵。
識別階段:
1)將待檢測的人臉影象T的差值臉投影到特徵空間,得到人臉T的特徵
2)從訓練集中一次取出每張人臉的特徵臉U。利用U與U的歐氏距離做相似性判定T是已知人臉或未知人臉。
根據Kyungnam Kim在其論文 Face Recognition using Principle Component Analysis 中所陳述,PCA人臉識別的基本思想是“…express the large 1-D vector of pixelsconstructed from 2-D facial image into the compact principal components of thefeature space(eigenspace projection).” 也就是從人臉影象中找出最能代表人臉的特徵空間。一個單個的人臉圖片對映到這個特徵空間得到這個特徵空間的一組係數(這張人臉圖片的特徵臉特徵)。如果兩張人臉圖片對映到這個特徵空間的係數差不多,就表示這兩張人臉是同一個人。從論文中我們也知道了特徵空間的計算方法“Eigenspace is calculated byidentifying the eigenvectors of the covariance matrix derived from a set offacial images(vectors). ”
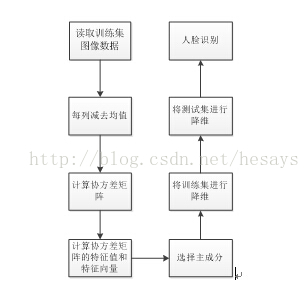
流程圖
資料庫:
測試資料庫為ORL_92x112,其中含40個人,每人10張圖片,共400張圖片。
下圖為40個人的第一張圖片。
訓練階段
1.1 一張人臉圖片在計算機表示為一個畫素矩陣,即是一個二維陣列,現在把這個二維陣列變成一維陣列,即把第一行後面的數全部新增到第一行。這樣一張圖片就能表示為一個向量d=(x1,x2......xn)。xn表示畫素。
1.2 現在訓練庫裡有m張人臉圖片,把這些圖片都表示成上述的向量形式,即d1,d2,。。。dm,把這m個向量取平均值得向量avg=(y1,y2......yn)。
得到平均影象:
1.3 用d1,d2...........dm分別減去avg後組成一個矩陣A,即矩陣A的第一行為d1-avg,後面類似。A的大小為m×n。因為找特徵空間不能基於一張圖片,而要在所有的人臉圖片提取出共同特徵,所以要取各個人臉向量到平均人臉向量的向量差。依據這個每個人臉圖片跟平均臉向量的向量差組成矩陣A,然後依據矩陣A來求解最特徵空間。
1.4.矩陣A乘以A的逆矩陣A‘得A的協方差矩陣B,B的大小m×m,求B的特徵向量。取最大的K個特徵向量組成新的矩陣T,T的大小m×k。
1.5 使用A’乘以T得到特徵臉C,C的大小n×k。
1.6 用圖片向量d乘以C得到圖片向量d在特徵臉的投影向量pn,有多少張圖片就有多少個pn。pn的大小1×k
探究各特徵值所佔有的能量數
2.1 第n個特徵值佔所有特徵值之和的百分比 (特徵值從小到大排列)。
2.2前n個特徵值佔所有特徵值之和的百分比 (特徵值從小到大排列)。
在實驗中,要求保留90%的能量,所以當取前57個特徵值得時候就可以滿足要求了。
測試階段
3.1.一張新的圖片也表示為d的向量,記為D,D的大小1×n
3.2. D乘以上面訓練得到的特徵臉C得到這個圖片向量D在C下的投影向量P,p的大小1×k。
3.3.計算p與上面所有的pn的向量距離,與p最小的那個向量所對應的人臉圖片跟這張新人臉圖片最像。
3.4.判別影象的相似性有兩種方法:一種是計算N維空間中影象間的距離,另一種是測量影象間的相似性。當測量距離時,距離應儘可能的小,一般選擇距離測試影象最近的訓練影象作為它所屬的類別,識別的方法和最初的影象匹配方法類似:將測試集中的每一幅降維影象與降維的訓練集進行匹配,然後將其分類到距離最小的訓練集頭像中,如果兩個頭像表示一個人,表示識別成功。而測量相似性時,影象應儘可能的相似,也就是說具有最大相似性的訓練影象類被認為是測試影象所屬的類別。本程式採用三階近鄰法。核心程式碼如下
執行程式後,將讀取40個人的後5張圖片,並進行比對,程式碼附錄給出。
可得到識別率為accuracy =0.8500;
參考文獻
[1]Kyungnam Kim. Face Recognition using Principle Component Analysis [J] . IEEESignal Processing Society,2002,9(2):40-42.
[2] 羅韻. 用Matlab進行PCA人臉識別 [N/OL] . 網易LOFTER,[2013-04-12] .http://blog.163.com/luoyun_dreamer/blog/static/215529070201331281538309/?suggestedreading
[3]haitao111313 . 基於PCA的人臉檢測 [N/OL] . CSDN部落格 , [2012-08-16] .http://blog.csdn.net/haitao111313/article/details/7875392
[4] Turk,M.A. ; Media Lab., MIT, Cambridge, MA, USA ; Pentland, A.P. Face Recognitionusing Eigenfaces [J] . IEEE Signal Processing Society,1991,7
附錄1.基於PCA的人臉識別的Matlab實現程式碼
function FaceRecognition
clear % calc xmean,sigma and its eigen decomposition
close all
allsamples=[];%所有訓練影象
for i=1:40
for j=1:5
if(i<10)
a=imread(strcat('E:\ORL_92x112\00',num2str(i),'0',num2str(j),'.bmp'));
else
a=imread(strcat('E:\ORL_92x112\0',num2str(i),'0',num2str(j),'.bmp'));
end
b=a(1:112*92); % b是行向量 1×N,其中N=10304,提取順序是先列後行,即從上到下,從左到右
b=double(b);
allsamples=[allsamples; b]; % allsamples 是一個M * N 矩陣,allsamples 中每一行資料代表一張圖片,其中M=200
end
end
samplemean=mean(allsamples); % 平均圖片,1 × N
figure%平均圖
imshow(mat2gray(reshape(samplemean,112,92)));
for i=1:200
xmean(i,:)=allsamples(i,:)-samplemean; % xmean是一個M × N矩陣,xmean每一行儲存的資料是“每個圖片資料-平均圖片”
end;
% figure%平均圖
% imshow(mat2gray(reshape(xmean(1,:),112,92)));
sigma=xmean*xmean'; % M * M 階矩陣
[v,d]=eig(sigma);
d1=diag(d);
[d2,index]=sort(d1); %以升序排序
cols=size(v,2);% 特徵向量矩陣的列數
for i=1:cols
vsort(:,i) = v(:, index(cols-i+1) ); % vsort 是一個M*col(注:col一般等於M)階矩陣,儲存的是按降序排列的特徵向量,每一列構成一個特徵向量
dsort(i) = d1( index(cols-i+1) ); % dsort 儲存的是按降序排列的特徵值,是一維行向量
end %完成降序排列 %以下選擇90%的能量
dsum = sum(dsort);
dsum_extract = 0;
p = 0;
while( dsum_extract/dsum < 0.9)
p = p + 1;
dsum_extract = sum(dsort(1:p));
end
a=1:1:200;
for i=1:1:200
y(i)=sum(dsort(a(1:i)) );
end
figure
y1=ones(1,200);
plot(a,y/dsum,a,y1*0.9,'linewidth',2);
grid
title('前n個特徵特佔總的能量百分比');
xlabel('前n個特徵值');
ylabel('佔百分比');
figure
plot(a,dsort/dsum,'linewidth',2);
grid
title('第n個特徵特佔總的能量百分比');
xlabel('第n個特徵值');
ylabel('佔百分比');
i=1; % (訓練階段)計算特徵臉形成的座標系
while (i<=p && dsort(i)>0)
base(:,i) = dsort(i)^(-1/2) * xmean' * vsort(:,i); % base是N×p階矩陣,除以dsort(i)^(1/2)是對人臉影象的標準化,特徵臉
i = i + 1;
end % add by wolfsky 就是下面兩行程式碼,將訓練樣本對座標系上進行投影,得到一個 M*p 階矩陣allcoor
%
% for i=1:20
% figure%平均圖
% b=reshape(base(:,i)',112,92);%
% imshow(mat2gray(b));
% end
allcoor = allsamples * base; accu = 0; % 測試過程
for i=1:40
for j=6:10 %讀入40 x 5 副測試影象
if(i<10)
if(j<10)
a=imread(strcat('E:\ORL_92x112\00',num2str(i),'0',num2str(j),'.bmp'));
else
a=imread(strcat('E:\ORL_92x112\00',num2str(i),num2str(j),'.bmp'));
end
else
if(j<10)
a=imread(strcat('E:\ORL_92x112\0',num2str(i),'0',num2str(j),'.bmp'));
else
a=imread(strcat('E:\ORL_92x112\0',num2str(i),num2str(j),'.bmp'));
end
end
b=a(1:10304);
b=double(b);
tcoor= b * base; %計算座標,是1×p階矩陣
for k=1:200
mdist(k)=norm(tcoor-allcoor(k,:));
end; %三階近鄰
[dist,index2]=sort(mdist);
class1=floor( index2(1)/5 )+1;
class2=floor(index2(2)/5)+1;
class3=floor(index2(3)/5)+1;
if class1~=class2 && class2~=class3
class=class1;
elseif class1==class2
class=class1;
elseif class2==class3
class=class2;
end;
if class==i
accu=accu+1;
end;
end;
end;
accuracy=accu/200 %輸出識別率