2016.04.16晚中山大學大學城校區（東校區）參加了多益網路的C++遊戲後臺開發的筆試。有幾道筆試題還是值得斟酌和記錄的，特記錄如下。比較可惜，因為回老家了，未能參加多益網路的面試。

1.試題彙總

題目一：
給定程式碼段int A[2][3]={1,2,3,4,5,6};那麼A[1][0]和*(*(A+1)+1)的值分別是什麼？
答：
A[1][0]=4，*(*(A+1)+1)=5。
這裡考察了對二維陣列的理解和指標運算。A[1][0]=4比較好理解。但是對二維陣列A進行指標運算時，我們要知道二維陣列A的型別是什麼，考察如下程式碼：

int A[2][3]={1,2,3,4,5,6};
cout<<"sizeof
 
(A):"<<sizeof(A)<<“ ”<<typeid(A).name()<<endl;

VS2012中程式碼輸出 sizeof(A):24 int [2][3]。可見二維陣列A的型別是int[2][3]，所以sizeof(A)=sizeof(int)*6=24。

知道了A的型別是int[2][3]之後，當我們對陣列A進行指標運算時，那麼A就會退化為指標，它的型別變為int(*)[3]，驗證程式碼如下：

cout<<"sizeof(A+1):"<<sizeof(A+1)<<" "<<typeid
 
(A+1).name()<<endl;
cout<<"sizeof(*(A+1)):"<<sizeof(*(A+1))<<endl;

輸出結果為：
sizeof(A+1):4 int (*)[3]
sizeof(*A):12 int [3]

所以*(A+1)表示的是二維陣列的第二行，其型別是int[3]。可將*(A+1)取個別名，容易理解，*(A+1)=int a[3]，此時在對變數*(A+1)進行指標運算時，就相當於對一維陣列a進行進行指標運算。那麼*(a+1)的值就是二維陣列A的第二行的第二個數5。

是有點繞，不過一定要好好理解，才能掌握陣列與指標之間的區別與聯絡。這裡有一點一定要記住：當對陣列進行指標運算時，其會退化為指標。

題目二：
下面程式碼的作用是什麼？

double x,ret=0;
for(int i=1;scanf("%lf",&x)==1;++i){
    ret+=(x-ret)/i;
}

答：
這段程式碼真的很精妙，其作用就是求標準輸入雙精度浮點數和的平均值。按照順序走幾遍迴圈就可以了。比如輸入的值為a，那麼結果ret=a，第二次輸入值為b，那麼:

以此類推，可以知道上面的程式碼是求輸入雙精度浮點數和的平均值。

題目三：
在一個平面座標系中，從方格（0,0）移動到方格（6,6），每次只能向上移動或者向右移動，且每次只能移動一個方格，且不能經過（2,3）和（4,4）兩個方格，有多少種移動的方式。
答：
這道題本質是組合問題。解題思路：
（1）算出從方格（0,0）到方格（6,6）總共有多少種移動的方式；
（2）減去經過（2,3）和（4,4）的所有路徑。

從方格（0,0）移動到方格（6,6）的移動次數是12次，每次都選擇向右還是向上。因此向右只能選擇6次，所以總的移動次數設為countAll=C612=924種。

按照上面的計算方式，（0,0）到（2,3）有C25種，再從（2,3）到（6,6）有C47種。所以經過方格（2,3）從（0,0）移動到（6,6）的移動方式countA=C25C47=350種。

同理，經過方格（2,3）從（0,0）移動到（6,6）的移動方式countB=C48C24=420種。

同理，同時經過（2,3）和（4,4）的移動方式countAB=C25C13C24=180種。

因為經過（2,3）的路徑中有可能經過（4,4），反之亦然。所以減去countA和countB時，會多減去一次同時經過（2,3）和（4,4）的移動方式數countAB，所以最終結果是：
count=countAll−countA−countB+countAB=924−350−420+180=334$。

題目四：
這是一道程式碼理解題。給定如下程式碼片段：

void getmemoney(char** p,int num){
    *p=(char*)malloc(num);
}

void test(void){
    char* str=NULL;
    getmemoney(&str,1000);
    strcpy(str,"hello");
    printf(str);
}

問執行test函式有什麼結果？

答：
這裡考察了兩點：
第一點：記憶體洩露；
第二點：strcpy函式的作用於特點。
執行test函式會列印輸出hello，且出現記憶體洩露。strcpy函式與是C語言標準庫函式，把從src地址開始且含有NULL結束符的字串複製到以dest開始的地址空間。這裡要注意的是字串拷貝結束後，會在目的地址空間最後新增空字元’\0’。

題目五：
這是一道程式設計題。題目如下：
第五套人民幣，中華人民共和國的紙幣有1元、5元、10元、20元、50元和100元。共6種，湊齊100元的一種組合是：五張1元+一張5元+兩張10元+一張20元+一張50元。請寫一個演算法，計算湊齊100元的組合的種類數。

答：
方法一：窮舉法
解題思路：
我們可以列舉所有可能情況。全部用1元來湊齊的話，需要一百張；全部用5元來湊的話，需要二十張；全部用10元，需要十張；全部用20元，需要五張；全部用50元，需要兩張，全部用100元，需要一張。

迭代實現：
因此我們可以採用多重迴圈迭代的方式來求出組成100元的所有可能性。參考如下程式碼：

int main(){
    int count=0; //組合種類數
    for(int a=0;a<=100;++a){
        for(int b=0;b<=20;++b){
            for(int c=0;c<=10;++c){
                for(int d=0;d<=5;++d){
                    for(int e=0;e<=2;++e){
                        for(int f=0;f<=1;++f){
                            if(1*a + 5*b + 10*c + 20*d + 50*e + 100*f==100)
                                count++;
                        }//end f:100元
                    }//end e：50元
                }//end d:20元
            }//end c:10元
        }//end b：5元
    }//end a:1元

    cout<<"count:"<<count<<endl;
}

程式輸出： count:344。表明有344種組合方式。

遞迴實現：
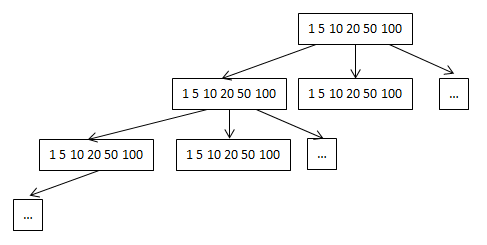
列舉所有可能的組合，我們可以採用遞迴的方式來實現。將所有可能的組合可以列舉成如下的六叉樹形結構：

我們深度遍歷這棵六叉樹，來統計湊夠100元的組合數。但是以遞迴的方式來深度遍歷這棵六叉樹時需要注意兩點：

第一點：回溯。對於每種面值累加厚，在退出當前節點回到上一層節點時需要進行回溯，即減去這一層節點的紙幣面值。

第二點：避免重複。在深度遍歷時，如果全部遍歷的話，會出現重複組合的情況。比如以面值1開始遞迴遍歷，有一種組合方式是1,1,1…1,5，從頭結點開始再以5開始遞迴遍歷會出現5,1,1,1…1。這兩種組合其實是同一種組合方式，如何避免這種重複計數呢？

以1開始遍歷，其實是統計了所有包含1組成100的左右可能情況。這時候，再以5開始遍歷的時候，我們就不應該再去遍歷包含1的所有可能的組合。所以要給定節點內的下標，表示當前遍歷時節點內的起始值是什麼。比如再以頭結點的5開始遍歷時，下面每一層節點內的遍歷起點都是從5開始，而不能從1開始。

參考如下程式碼：

int rmb[6]={1,5,10,20,50,100};
int count=0;//組合數

//index：表示第幾個紙幣，即節點內下標
void getCombinationNum(int& sum,int index){
    for(int i=index;i<6;++i){
        sum+=rmb[i];
        if(sum<100)
            getCombinationNum(sum,i);
        if(sum==100){
            ++count;
        }
        sum-=rmb[i]; //回溯
    }
}

int main(){
    int sum=0; //幣值累加和
    getCombinationNum(sum,0);
    cout<<"count:"<<count<<endl;
}

程式輸出：count：344種。

遞迴與迭代實現的對比：
使用遞迴的方式來實現窮舉所有可能的組合，程式碼實現上較為簡潔，但是遞迴帶來的多重的函式呼叫增加了執行時開銷，效率次於迭代實現，並且不太容易理解。所以建議使用迭代的方式來實現窮舉。

方法二：動態規劃法
考察組成100元的方式，可以從高面值往低面值開始拆分。對於100元面值的紙幣，組成100元的方式要麼包含100元面值的紙幣，要麼不包含這兩種情況。

所以可以設f(n,j)表示價值為n的金額由包含第0到第j種面值組成的所有情況數。那麼f(n,j)分為兩種情況，包含第j種面值，和不包含第j種面值情況，那麼f(n,j)=f(n-v[j],j)+f(n,j-1)。其中f[n,j-1]表示沒有第j種紙幣的情況的總和，f(n-v[j],j)表示去掉一張第j中紙幣面值後剩餘面值由第0到第j種面值組成的所有情況數。特別的，當n=0時，f(0,j)=1。

有了上面的遞迴式，我們知道f(100,5)就是我們要求的組成100元由第0種紙幣1元到第5種紙幣100元組成的種類數。

實現參考如下程式碼：

const int v[6] = {1,5,10,20,50,100};

int f(int n, int w)
{
    if(n<0) return 0;
    if(n==0) return 1;
    if(w<0) return 0;

    return f(n, w-1) + f(n-v[w], w);
}

int main(){
    cout<<"count:"<<f(100,5)<<endl;
}

輸出結果：count:344。

小結

終於寫完了，歷時兩天。裡面的一些東西還是不錯的。尤其是最後一個程式設計題。包含了一些演算法思想，值得大家深思。在程式設計時，思路很重要，有了正確的思路，才能寫出正確的程式碼。

參考文獻