AC自動機步驟詳解
阿新 • • 發佈:2019-02-04
AC自動機
演算法意義:
求多個字串是否在主串中出現過。可依據情況分別求出出現次數,出現位置等。學習基礎:
要搞懂AC自動機,先得有模式樹(字典樹)Trie和KMP模式匹配演算法的基礎知識。AC自動機的構造:
1.構造一棵Trie,作為AC自動機的搜尋資料結構。2.構造fail指標,使當前字元失配時跳轉到具有最長公共前後綴的字元繼續匹配。如同 KMP演算法一樣, AC自動機在匹配時如果當前字元匹配失敗,那麼利用fail指標進行跳轉。由此可知如果跳轉,跳轉後的串的字首,必為跳轉前的模式串的字尾並且跳轉的新位置的深度(匹配字元個數)一定小於跳之前的節點。所以我們可以利用 bfs在 Trie上面進行 fail指標的求解。
3.掃描主串進行匹配。
AC自動機詳講:
我們給出5個單詞,say,she,shr,he,her。給定字串為yasherhs。問多少個單詞在字串中出現過?一、構建trie樹
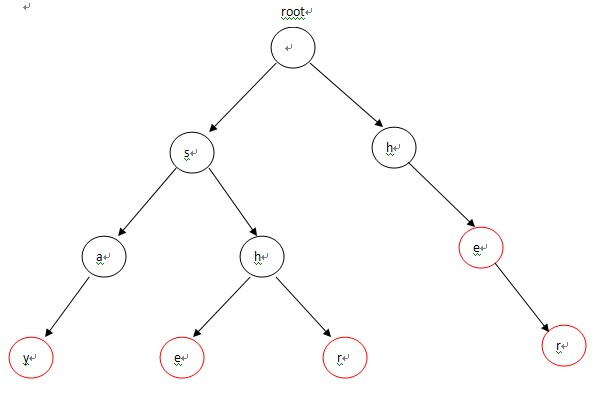
首先這個trie樹的每個節點必須包含以下元素:
1.一個失敗指標,記錄匹配失敗後將要跳轉的節點。 程式碼中的node *fail;
2.26個兒子節點,記錄的是26個兒子,編號代表下一個字母的值。 程式碼中的node *child[26];
3.一個標記當前是不是一個單詞的結尾。程式碼中的int count;
4.順便呼叫構造方法給每個節點賦初值。
節點程式碼:
struct node { node *fail; node *child[26]; int count; node() { fail=NULL; count =0; memset(child,NULL,sizeof(child)); } };
建樹程式碼:
void insert(node *t,char *p)
{
int index;
while(*p!='\0')
{
index=*p-'a';
if(t->child[index]==NULL)
t->child[index]=new node();
t=t->child[index];
p++;
}
t->count=1;
}二、構建失敗指標
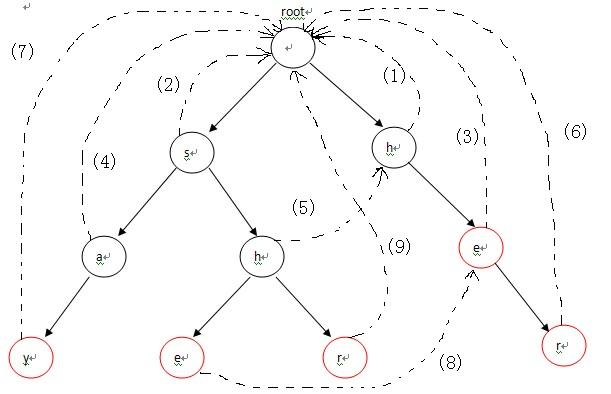
root的失敗指標為NULL。
求某個節點的失敗指標的方法:
1.判斷他的父親節點是不是root。
2.若是,他的失敗指標指向的是root。
3.若不是,找到父親節點失敗指標所指的節點的子節點是否含有和所求節點相同的字母。例如,上圖中求she中e的失敗指標:e的父親節點h的失敗指標是her中的h,而h的兒子節點有和e相同的節點。
4.如果含有,失敗指標就是找到的那個和本節點相同的節點,如she中e的失敗指標就是he中的e節點。
5.如果沒有,找到他父親的失敗指標的失敗指標繼續3.。直到到root節點都沒找到的話,就令本解點的失敗指標為root。如shr的r節點,他的父親節點h的失敗指標是her中的h。其子節點中只有e,沒有r所以再求her中h的失敗指標,他是root,所以shr中r的失敗指標是root。
構建失敗指標部分程式碼如下:
void ac(node *t)
{
t->fail=NULL;
q.push(t);
node *temp;
node *tmp;
int i;
while(!q.empty())
{
temp=q.front();
q.pop();
for(i=0;i<26;i++)
{
if(temp->child[i]!=NULL)
{
if(temp==t)
temp->child[i]->fail=t;
else
{
tmp=temp->fail;
while(tmp!=NULL)
{
if(tmp->child[i]!=NULL)
{
temp->child[i]->fail=tmp->child[i];
break;
}
tmp=tmp->fail;
}
if(tmp==NULL)
temp->child[i]->fail=t;
}
q.push(temp->child[i]);
}
}
}
}
三、掃描主串進行匹配。
構造好Trie和失敗指標後,我們就可以對主串進行掃描了。這個過程和KMP演算法很類似,但是也有一定的區別,主要是因為AC自動機處理的是多串模式,需要防止遺漏某個單詞,所以引入temp指標。
匹配過程分兩種情況:
(1)當前字元匹配,表示從當前節點沿著樹邊有一條路徑可以到達目標字元,此時只需沿該路徑走向下一個節點繼續匹配即可,目標字串指標移向下個字元繼續匹配;
(2)當前字元不匹配,則去當前節點失敗指標所指向的字元繼續匹配,匹配過程隨著指標指向root結束。重複這2個過程中的任意一個,直到模式串走到結尾為止。
看一下模式匹配這個詳細的流程:
其中模式串為yasherhs。對於i=0,1。Trie中沒有對應的路徑,故不做任何操作;
i=2,3,4時,指標p走到左下節點e。因為節點e的count資訊為1,所以cnt+1,並且講節點e的count值設定為-1,表示改單詞已經出現過了,防止重複計數。
最後temp指向e節點的失敗指標所指向的節點繼續查詢,以此類推,最後temp指向root,退出while迴圈。
這個過程中count增加了2。表示找到了2個單詞she和he。
當i=5時,程式進入第5行,p指向其失敗指標的節點,也就是右邊那個e節點,隨後在第6行指向r節點,r節點的count值為1,從而count+1,迴圈直到temp指向root為止。
最後i=6,7時,找不到任何匹配,匹配過程結束。
程式碼如下:
int query(node *t,char *p)
{
int index,cnt=0;
node *tmp;
while(*p!='\0')
{
index=*p-'a';
while(t->child[index]==NULL &&t->fail!=NULL)
t=t->fail;
if(t->child[index]!=NULL)
{
t=t->child[index];
tmp=t;
while(tmp->count==1)
{
cnt++;
tmp->count=-1;
tmp=tmp->fail;
}
}
p++;
}
return cnt;
}
void del(node *root)
{
for(int i=0;i<26;i++)
if(root->child[i]!=NULL)
del(root->child[i]);
delete root;
root=NULL;
}完整程式碼:
#include <stdio.h>
#include <string.h>
#include <queue>
using namespace std;
struct node
{
node *fail;
node *child[26];
int count;
node()
{
fail=NULL;
count =0;
memset(child,NULL,sizeof(child));
}
};
char s1[51];
char s2[1000001];
queue <node*> q;
void insert(node *t,char *p)
{
int index;
while(*p!='\0')
{
index=*p-'a';
if(t->child[index]==NULL)
t->child[index]=new node();
t=t->child[index];
p++;
}
t->count=1;
}
void ac(node *t)
{
t->fail=NULL;
q.push(t);
node *temp;
node *tmp;
int i;
while(!q.empty())
{
temp=q.front();
q.pop();
for(i=0;i<26;i++)
{
if(temp->child[i]!=NULL)
{
if(temp==t)
temp->child[i]->fail=t;
else
{
tmp=temp->fail;
while(tmp!=NULL)
{
if(tmp->child[i]!=NULL)
{
temp->child[i]->fail=tmp->child[i];
break;
}
tmp=tmp->fail;
}
if(tmp==NULL)
temp->child[i]->fail=t;
}
q.push(temp->child[i]);
}
}
}
}
int query(node *t,char *p)
{
int index,cnt=0;
node *tmp;
while(*p!='\0')
{
index=*p-'a';
while(t->child[index]==NULL &&t->fail!=NULL)
t=t->fail;
if(t->child[index]!=NULL)
{
t=t->child[index];
tmp=t;
while(tmp->count==1)
{
cnt++;
tmp->count=-1;
tmp=tmp->fail;
}
}
p++;
}
return cnt;
}
void del(node *root)
{
for(int i=0;i<26;i++)
if(root->child[i]!=NULL)
del(root->child[i]);
delete root;
root=NULL;
}
int main()
{
int n,m;
scanf("%d\n",&n);
while(n--)
{
node *root=new node();
scanf("%d\n",&m);
while(m--)
{
gets(s1);
insert(root,s1);
}
gets(s2);
ac(root);
printf("%d\n",query(root,s2));
del(root);
}
return 0;
}