[資料結構]二叉樹及其遍歷
二叉樹
Keyword
二叉樹的概念,特性及二叉樹的前序(pre-order traversal),中序(in-order traversal),後序(post-order traversal)遍歷以及廣度優先遍歷(Breadth First Search),深度優先遍歷(Depth First Search),二叉樹的Morris遍歷。
二叉樹的基本概念
二叉樹就是每個節點最多有兩個子樹的樹結構,其兩個子樹通常被稱為左子樹(left subtree)和右子樹(right subtree)。
二叉樹的每個節點最多可能存在兩棵子樹(既不可能存在度大於2的節點),兩個子樹有左右之分且次序不能顛倒。
二叉樹的第i層至多有2^(i-1)個結點,深度為k的二叉樹至多有2^k-1個結點。
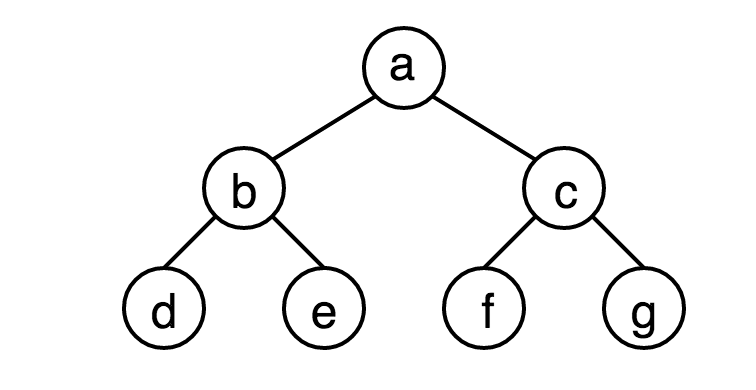
滿二叉樹(Full Binary Tree)指的是深度為k且有2^k-1個結點的二叉樹。既除去葉子結點外其餘結點均具有左右孩子。下圖為滿二叉樹。
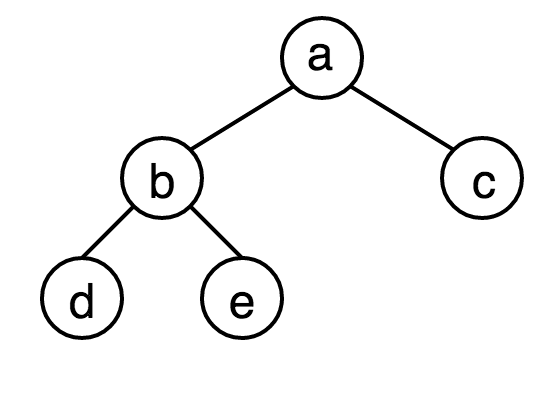
完全二叉樹(Complete Binary Tree)指的是除最深一層層外其餘層既構成一個滿二叉樹的樹,最大層的葉子結點全部靠左分佈。具有n個結點的完全二叉樹的結點與滿二叉樹中前n個結點一一對應。下圖為完全二叉樹。
對於完全二叉樹,若以一個數組array來表示其按層從高到低,從左到右遍歷的結果,設一個結點為i,則其父結點為i/2,其左子結點為2*i,其右子結點為2*i+1
二叉樹的儲存結構
二叉樹的鏈式儲存結構定義如下:
/*
* Definition of Binary Tree
*/
public class BinaryTreeNode{
int data;
BinaryTreeNode leftchild;
BinaryTreeNode rightchild;
BinaryTreeNode (int x){
data = x;
}
/** construct binary tree with an array
* recursive method
* @param 二叉樹的遍歷
遍歷即按給某種順序訪問所有的二叉樹中的結點1次。
按訪問結點的順序可以分為:
- 前序遍歷:根結點–>左子樹–>右子樹
- 中序遍歷:左子樹–>根結點–>右子樹
- 後續遍歷:左子樹–>右子樹–>根節點
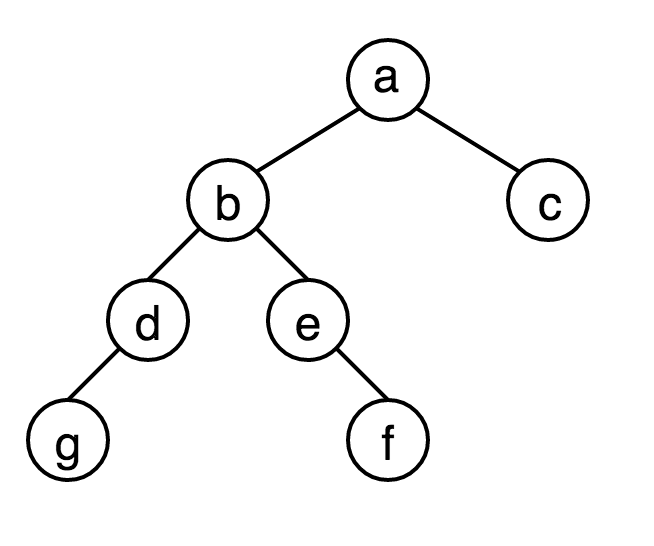
例如求以下這棵樹的幾種遍歷:
前序遍歷:abdgefc
中序遍歷:gdbefac
後序遍歷:gdfebca
廣度優先遍歷:abcdegf
深度優先遍歷:abdgefc
遍歷的實現
遞迴實現
前序遍歷
/*
* Pre-order traversal of a binary tree recursively
*/
public void preOrderTrav(BinaryTreeNode root) {
if (root != null) {
System.out.println(root.data);
preOrderTrav(root.leftchild);
preOrderTrav(root.rightchild);
}
}中序遍歷
/*
* In-order traversal of a binary tree recursively
*/
public void inOrderTrav(BinaryTreeNode root) {
if (root != null) {
inorderTrav(root.leftchild);
System.out.println(root.data);
inorderTrav(root.rightchild);
}
}後序遍歷
/*
* Post-order traversal of a binary tree recursively
*/
public void postOrderTrav(BinaryTreeNode root) {
if (root != null) {
postOrderTrav(root.leftchild);
postOrderTrav(root.rightchild);
System.out.println(root.data);
}
}非遞迴實現
當採用非遞迴實現的時候,我們考慮到遍歷過根結點的子結點之後還要再回來訪問根結點,所以我們需要將訪問過的根結點存起來。考慮到其後進先出的特性,我們需要用棧(stack)來儲存
前序遍歷
import java.util.Stack;
public void preorderTrav(BinaryTreeNode root){
Stack<BinaryTreeNode> stack = new Stack<BinaryTreeNode>();
if (root == null){
System.out.println("Empty Tree!");
}
else{
while (root != null || !stack.empty()) {
while (root != null){
System.out.println(root.data);
stack.push(root);
root = root.leftchild;
}
root = stack.pop();
root = root.rightchild;
}
}
}中序遍歷
import java.util.Stack;
public void inorderTrav(BinaryTreeNode root){
Stack<BinaryTreeNode> stack = new Stack<BinaryTreeNode>();
if (root == null){
System.out.println("Empty Tree!");
}
else {
while (root != null || !stack.empty()){
while (root != null){
stack.push();
root = root.leftchild;
}
root = stack.pop();
System.out.println(root.data);
root = root.rightchild;
}
}
}後序遍歷
在後序遍歷中,給定一個根結點,我們需要先訪問根結點的左子樹,然後訪問根結點的右子樹,最後訪問根結點。因此在迭代過程中我們需要儲存一個prev 變數來儲存前一步中訪問過的結點,從而判斷這一步應該繼續向下訪問還是向上訪問根結點。遍歷的過程有如下三種情況:
從棧頂peek一個元素為curr:
- 如果
prev == null或者prev.left == curr或者prev.right == curr,則有如下情況。根據後序遍歷的順序,所有這幾種情況下,如果當前結點的左子樹不為空,則我們將當前節點的左孩子放入棧中並繼續這個迴圈。如果當前結點的左孩子為空且右孩子不為空,則將當前結點的右孩子放入棧中並繼續迴圈。如果當前結點的左右孩子均為空,則當前節點為一個葉子結點,我們應當將當前結點從棧中刪除並記錄其值。
- 如果
prev == null,則我們之前並未訪問任何結點,當前curr所在結點為二叉樹的根結點。 - 如果
prev.left == curr,則我們之前訪問了curr的父節點。 - 如果
prev.right == curr,則我們之前訪問了curr的父節點。
- 如果
- 如果
prev == curr.left,則代表我們前一步訪問了當前結點的左孩子。如果當前結點的右孩子不為空,則我們將當前結點的右孩子放入棧中,並繼續迴圈。反之,如果當前結點的右孩子為空,我們應當記錄當前結點的值並將其從棧中刪除。 - 如果
prev == curr.right,則代表我們前一步中訪問了當前結點的右孩子。根據後序遍歷的順序,我們應當記錄當前結點的值並從棧中將其刪除。
import java.util.*;
public class IterativePostOrder {
public List<Integer> postOrderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
postOrderTraversal(root, list);
return list;
}
private void postOrderTraversal(TreeNode root, List<Integer> list) {
Deque<TreeNode> deque = new ArrayDeque<>();
if (root == null) {
return;
}
deque.push(root);
TreeNode prev = null;
while (!deque.isEmpty()) {
TreeNode curr = deque.peek();
if (prev == null || prev.left == curr || prev.right == curr) {
if (curr.left != null) {
deque.push(curr.left);
} else if (curr.right != null) {
deque.push(curr.right);
} else {
deque.pop();
list.add(curr.val);
}
} else if (prev == curr.left) {
// previously visited current's left child
if (curr.right != null) {
deque.push(curr.right);
} else {
deque.pop();
list.add(curr.val);
}
} else if (prev == curr.right) {
// previously visited current's right child
// hence we should visit the current node based on post order
deque.pop();
list.add(curr.val);
}
prev = curr;
}
}
}廣度優先遍歷(BFS)
廣度優先遍歷也就是按層次遍歷二叉樹,依次遍歷其根結點,左孩子和右孩子。在這種遍歷方式下,左右子樹按順序輸出,所以需要採用先進先出的佇列來儲存。
其演算法如下:
- 訪問初始結點root並標記其為已訪問
- 將root存入佇列
- 當佇列非空時,繼續執行演算法,否則演算法結束
- 取得對列頭部的結點u,出佇列
- 查詢結點u的第一個子結點w
- 如果結點u的子結點不存在,則轉到步驟3。否則迴圈執行以下步驟:
- 若結點w尚未被訪問,則訪問結點w並標記為已訪問
- 將結點w存入佇列
- 查詢結點u的下一個子結點,轉到步驟6
以下是廣度優先遍歷的程式碼:
import java.util.Queue;
import java.util.LinkedList;
public void BFS(BinaryTreeNode root){
if (root == null){
System.out.println("Empty Tree!");
return;
}
Queue<BinaryTreeNode> queue = new LinkedList<BinaryTreeNode>();
queue.add(root);
while (!queue.isEmpty()){
BinaryTreeNode node = queue.remove();
System.out.println(node.data);
if (node.leftchild != null){
queue.add(node.leftchild);
}
if (node.rightchild != null){
queue.add(node.rightchild);
}
}
}深度優先遍歷(DFS)
與廣度優先遍歷中的按層次遍歷不同,深度優先遍歷是沿著每一個樹的分支走到底然後再返回遍歷其餘分支。其策略就是先訪問一個結點,然後以這個結點為根訪問其子結點,既優先縱向挖掘深入。由於二叉樹不存在環,所以我們不需要標記每一個結點是否已被訪問過。又由於其遍歷特點,我們需要後進先出的訪問儲存的結點。所以我們使用棧來儲存。
其演算法如下(非遞迴):
- 訪問初始結點root,並標記其為已訪問
- 查詢結點root的子結點並將這些子結點存入棧中
- 判斷棧是否為空,如果為空結束迴圈,如果不為空則繼續執行演算法
- 取出棧頂結點,標記為已訪問並查詢其子結點
- 若子結點不存在則轉到步驟3,否則迴圈執行以下步驟:
- 若結點尚未被訪問,則將其存入棧中
- 查詢下一個子結點並回到步驟6
對應的程式碼如下:
import java.util.Stack;
public void DFS(BinaryTreeNode root){
if (root == null){
System.out.println("Empty Tree!");
return;
}
Stack<BinaryTreeNode> stack = new Stack<BinaryTreeNode>();
stack.push(root);
while (!stack.isEmpty()){
BinaryTreeNode node = stack.pop();
System.out.println(node.data);
if (node.leftchild != null){
stack.push(node.leftchild);
}
if (node.rightchild != null){
stack.push(node.rightchild);
}
}
}深度優先遍歷也可以用遞迴解決,運用遞迴的深度優先遍歷演算法如下:
- 訪問初始結點root並標記為已訪問
- 查詢該結點的子結點
- 若子結點存在,則執行步驟4,否則演算法結束
- 若子結點未被訪問,則以子結點為初始結點進行遞迴深度優先遍歷
- 查詢下一個子結點,轉到步驟3
public void recursiveDFS(BinaryTreeNode root){
if (root == null){
System.out.println("Empty Tree!");
return;
}
System.out.println(root.data);
if (root.leftchild != null){
recursiveDFS(root.leftchild);
}
if (root.rightchild != null){
recursiveDFS(root.rightchild);
}
}二叉樹的Morris遍歷
以上的遞迴演算法或者棧迭代演算法遍歷二叉樹所需的時間和空間複雜度均為O(n)。但還存在一種更為巧妙的Morris遍歷演算法(Morris Traversal),其時間複雜度為O(n),但空間複雜度為O(1)。
Morris演算法只需常數空間且不會改變二叉樹的形狀(中間過程會改變)。
要使用O(1)空間進行遍歷,最大的難度在於怎樣返回父節點(假設結點中沒有指向父節點的指標)。為了解決這個問題,Morris演算法用到了線索二叉樹的概念(threaded binary tree)。在Morris演算法中不需要額外為每個二叉樹分配指標指向其前驅(predecessor)和後繼結點(successor),只需要用結點中的左右空指標指向某種順序遍歷下的前驅或者後繼結點即可。
中序遍歷的Morris演算法
- 如果當前結點的左孩子為空,則輸出當前結點並將其右孩子作為當前結點。
- 如果當前結點的左孩子不為空,則在當前結點的左子樹中找到當前結點在中序遍歷下的前驅結點。
- 如果前驅結點的右孩子為空,則將前驅結點的右孩子設為當前節點,當前結點更新為當前結點的左孩子。
- 如果前驅結點的右孩子為當前結點,則將其右孩子重新設為空(恢復樹的形狀)。輸出當前節點,當前結點更新為當前結點的右孩子。
- 重複以上1,2步驟直到當前結點為空。
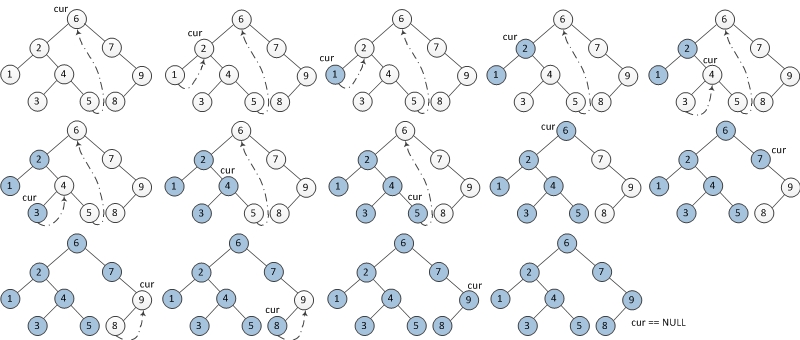
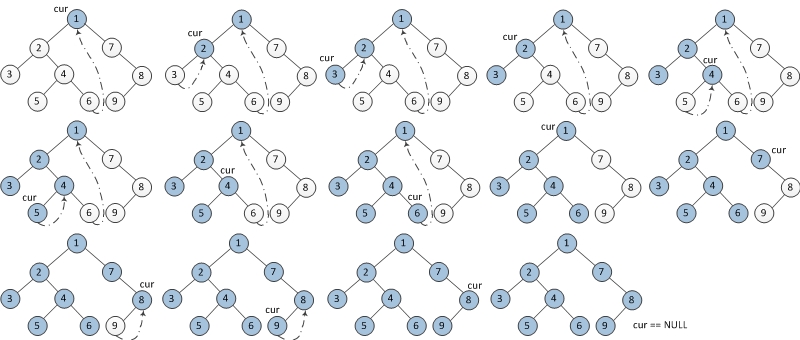
下圖表示了每一步迭代的結果,從左到右,從上到下。其中cur代表當前結點,藍色結點代表已輸出的結點。
中序Morris遍歷的程式碼如下:
public void InorderMorrisTraversal(BinaryTreeNode root){
BinaryTreeNode prev = null;
BinaryTreeNode cur = root;
if (cur == null){
System.out.println("Empty Tree!");
return;
}
while (cur != null){
if (cur.left == null){ //1
System.out.println(cur.data);
cur = cur.right;
}
else {
//find predecessor
prev = cur.left;
while (prev.right != null && prev.right != cur){
prev = prev.right;
}
if (prev.right == null){ //2a
prev.right = cur;
cur = cur.left;
}
else { //2b
System.out.println(cur.data);
prev.right = null;
cur = cur.right;
}
}
}
}複雜度分析:
空間複雜度:只使用了cur和prev兩個變數。所以空間複雜度是O(1)
時間複雜度:解決時間複雜度的關鍵是尋找前驅結點的程式碼
while (prev.right != null && prev.right != cur){
prev = prev.right;
}直覺上看,這段程式碼和二叉樹的深度有關。二叉樹深為logn,所以需要O(nlogn)時間。實際上,考慮到n個結點的二叉樹中共有n-1條邊,而每條邊最多隻走兩次(一次遍歷到達cur結點進過該邊,一次尋找前驅結點prev經過該邊),所以實際執行時間為O(n)。
前序遍歷的Morris演算法
前序遍歷與中序遍歷類似,只不過輸出結點值得位置不同。演算法如下:
- 如果當前結點的左孩子為空,則輸出當前結點值並將其右孩子作為當前結點
- 如果當前結點的左孩子不為空,則在當前結點的左子樹中找到當前節點在中序遍歷下的前驅結點
- 如果前驅結點的右孩子為空,則將前驅結點的右孩子設定為當前結點,並輸出當前結點(在此處輸出,是與中序遍歷的唯一不同)。當前結點設定為當前結點的右孩子。
- 如果前驅結點的右孩子為當前結點,則將其右孩子設定為空。當前結點更新為當前結點的右孩子
- 重複1,2兩個步驟知道當前結點為空
圖示:
二叉樹的前序Morris遍歷Java程式碼如下:
public void preorderMorrisTraversal(BinaryTreeNode root){
BinaryTreeNode prev;
BinaryTreeNode cur = root;
if (root == null){
System.out.println("Empty Tree!");
return;
}
while (cur != null){
if (cur.left == null){ //1
System.out.println(cur.data);
cur = cur.right;
}
else {
prev = cur.left;
while (prev.right != null && prev.right != cur){ //find the predecessor of the current node
prev = prev.right;
}
if (prev.right == null){ //2a
prev.right = cur;
System.out.println(cur.data); //the only difference with inorder traversal
cur = cur.left;
}
else { //2b
prev.right = null;
cur = cur.right;
}
}
}
}複雜度分析:
與中序遍歷類似,空間複雜度為O(1),時間複雜度為O(n)。