BZOJ
UOJ正常版本
UOJ變態版本
Description
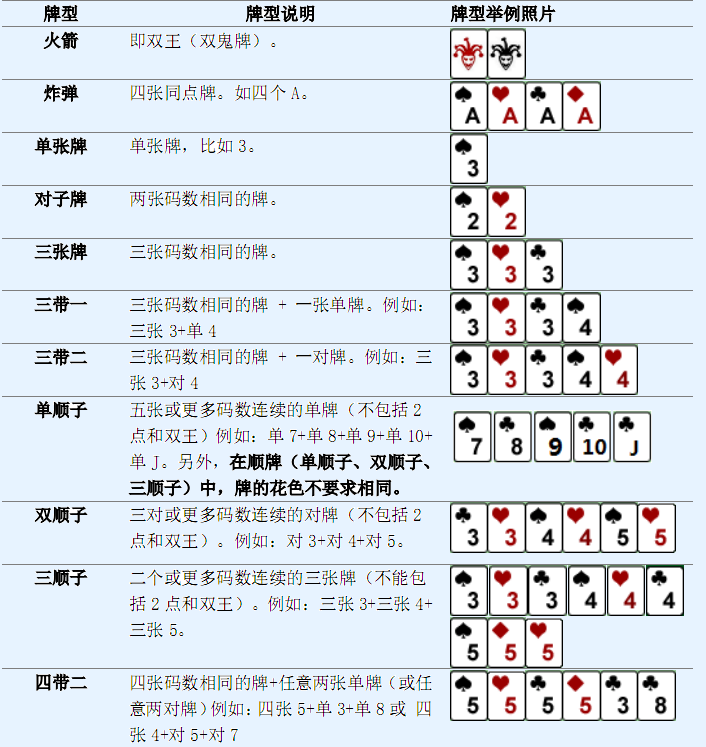
牛牛最近迷上了一種叫鬥地主的撲克遊戲。鬥地主是一種使用黑桃、紅心、梅花、方片的A到K加上大小王的共54張牌來進行的撲克牌遊戲。在鬥地主中，牌的大小關係根據牌的數碼錶示如下：3<4<5<6<7<8<9<10<J<Q<K<A<2<小王<大王，而花色並不對牌的大小產生影響。每一局遊戲中，一副手牌由n張牌組成。遊戲者每次可以根據規定的牌型進行出牌，首先打光自己的手牌一方取得遊戲的勝利。現在，牛牛隻想知道，對於自己的若干組手牌，分別最少需要多少次出牌可以將它們打光。請你幫他解決這個問題。需要注意的是，本題中游戲者每次可以出手的牌型與一般的鬥地主相似而略有不同。具體規則如下：

接下來T組資料，每組資料N行，每行一個非負整數對Ai,Bi，表示一張牌，其中Ai表示牌的數碼,Bi表示牌的花色，中間用空格隔開。特別的，我們用1來表示數碼A，11表示數碼J，12表示數碼Q，13表示數碼K；黑桃、紅心、梅花、方片分別用1-4來表示；小王的表示方法為01，大王的表示方法為02。
Output
共T行，每行一個整數，表示打光第T組手牌的最少次數。

Sample Input

1 8

7 4

8 4

9 1

10 4

11 1

5 1

1 4

1 1

Sample Output

3

HINT

共有1組手牌，包含8張牌：方片7，方片8，黑桃9，方片10，黑桃J，黑桃5，方

片A以及黑桃A。可以通過打單順子（方片7，方片8，黑桃9，方片10，黑桃J），單張

牌（黑桃5）以及對子牌（黑桃A以及方片A）在3次內打光。

T<=10
N<=23

題解：
嗯，我的思路是貪心，在極限資料是過不了的，所以在UOJ最後一組資料過不了，如想看完全正確的思路請看別人的狀壓DP的程式碼。
不過既然是貪心和迭代加深那麼優點，當然是程式碼量短理解簡單，沒有高階的演算法。

嗯，思路就是首先計算四帶二 ，三帶二，四帶二，三帶一能有多要對，然後暴力的計算拆出打三順子，之後打四帶二 ，三帶二，四帶二，三帶一能有多少對，然後暴力的計算拆出打雙個順子，之後打四帶二 ，三帶二，四帶二，三帶一能有多少對，最後暴力的拆出打單順子，之後打四帶二 ，三帶二，四帶二，三帶一能有多少對，因為我們把能一次打更多的先打，這個貪心的思路，可能會有一點點的問題，所以會被極限資料卡掉，但是當時比賽很多人都是選的這個思路，因為簡單，而且不容易打錯。因為是隨機的資料，最後就是拼人品諾，還是有人被扣了5分的。。。。
但是這個程式碼正常的都是AC了的。而且跑的超級快。

#include <iostream>
#include <cstring>
#include <string>
#include <cstdio>
using namespace std;

const int MAXN = 18;

int T,N,ans;
int A[MAXN],cnt[MAXN]; //A 是 碼數  CNT 是 各個數量的多少 

inline int read(){
    int x = 0;char ch = getchar();
    while(ch < '0' || '9' < ch){ch = getchar();}
    while('0' <= ch&& ch <='9'){x = x * 10 + ch - '0';ch = getchar();}
    return x;
}

inline int calc(int x[])
{
    memset(cnt,0,sizeof(cnt));

    int res = 0;

    for(int i = 1;i < MAXN;i++) cnt[ A[i] ]++;
    while(cnt[4] && cnt[2] >= 2) res++,cnt[4]--,cnt[2] -= 2;//四帶二 
    while(cnt[3] && cnt[2] >= 1) res++,cnt[3]--,cnt[2] -= 1;//三帶二 
    cnt[ A[0] ]++;
    while(cnt[4] && cnt[1] >= 2) res++,cnt[4]--,cnt[1] -= 2;//四帶二 
    while(cnt[3] && cnt[1] >= 1) res++,cnt[3]--,cnt[1] -= 1;//三帶一
    while(cnt[4] >= 2) res++,cnt[4] -= 2;
    return res + cnt[4] + cnt[3] + cnt[2] + cnt[1];
}

inline void dfs(int x[],int step){
    if(step > ans) return;
    ans = min(ans,step + calc(x));

    for(int i = 2;i < MAXN;i++){    //三順子
        int j; 
        for(j = i;x[j] >= 3;j++);

        if(j - i >= 2){             //湊成三順子 
            for(int t = j;t - i >= 2;t--){
                for(int k = i;k < t;k++) x[k] -= 3;
                dfs(x,step+1);
                for(int k = i;k < t;k++) x[k] += 3;
            }
        }
    }

    for(int i = 2;i < MAXN;i++){    //雙順子 
        int j;
        for(j = i;x[j] >= 2;j++);

        if(j - i >= 3){             //湊成雙順子 
            for(int t = j;t - i >= 3;t--){
                for(int k = i;k < t;k++) x[k] -= 2;
                dfs(x,step+1);
                for(int k = i;k < t;k++) x[k] += 2;
            }
        }
    }

    for(int i = 2;i < MAXN;i++){    //單順子 
        int j;
        for(j = i;x[j] >= 1;j++);

        if(j - i >= 5){             //湊成單順子 
            for(int t = j;t - i >= 5;t--){
                for(int k = i;k < t;k++) x[k] -= 1;
                dfs(x,step+1);
                for(int k = i;k < t;k++) x[k] += 1;
            }
        }
    }
}

int main(){
    T = read();N = read();

    while(T--){
        memset(A,0,sizeof(A));
        for(int i = 1;i <= N;i++){
            int w = read(),c = read();
            if(w == 1) w = 13;
            else if(w) w--;
            A[w]++;
        }
        ans = calc(A);
        dfs(A,0);
        printf("%d\n",ans);
    }

    return 0;
}