R語言中的概率論和數理統計
前言
1.大部分參考張丹(Conan)的R的極客理想系列文章《概率基礎和R語言》,對此表示感謝。
(http://blog.fens.me/r-probability/)
2.補充、解釋和學習,記錄並便於今後的查詢。
目錄
- 隨機變數
- 隨機變數的數字特徵
- 極限定理
一、隨機變數
(一)、什麼是隨機變數?
1.定義
隨機變數(random variable)表示隨機現象各種結果的實值函式。隨機變數是定義在樣本空間S上,取值在實數域上的函式,由於它的自變數是隨機試驗的結果,而隨機實驗結果的出現具有隨機性,因此,隨機變數的取值具有一定的隨機性。
2.R程式:生成一個在(0,1,2,3,4,5)的隨機變數
> S<-1:5
> sample(S,1)
[1] 2
> sample(S,1)
[1] 3
> sample(S,4)
[1] 3 5 4 1
#sample(x=x,size=5,replace=T),其中size指定抽樣的次數,“replace”就是重複的意思。即可以重複對元素進行抽樣,也就是所謂的有放回抽樣。(二)、離散型隨機變數
1.定義
如果隨機變數X的全部可能的取值只有有限多個或可列無窮多個,則稱X為離散型隨機變數。
2.R程式:生成樣本空間為(1,2,3)的隨機變數X,X的取值是有限的
> S<-1:3 (三)、連續型隨機變數
1.定義
隨機變數X,取值可以在某個區間內取任一實數,即變數的取值可以是連續的,這隨機變數就稱為連續型隨機變數
2.定義R程式:生成樣本在空間(0,1)的連續隨機函式,取10個值
> runif(10,0,1)
[1] 0.3819569 0.7609549 0.6692581 0.6314708 0.5552201 0.8225527 0.7633086 0.4667188 0.1883553
[10] 0.3741653
#1.runif(n,min=0,max=1)函式的規則:
n表示生成的隨機數數量,min 二、隨機變數的數字特徵
(一)、數學期望(mathematical expectation)
1.離散型隨機變數:一切可能的取值xi與對應的概率Pi(=xi)之積的和稱為該離散型隨機變數的數學期望,記為E(x)。數學期望是最基本的數學特徵之一。它反映隨機變數平均取值的大小。
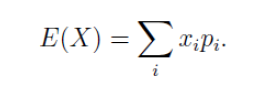
R程式:計算樣本(1,2,3,7,21)的數學期望
> S<-c(1,2,3,7,21)
> mean(S)
[1] 6.82.連續型隨機變數:若隨機變數X的分佈函式F(x)可表示成一個非負可積函式f(x)的積分,則稱X為連續性隨機變數,f(x)稱為X的概率密度函式,積分值為X的數學期望,記為E(X)。
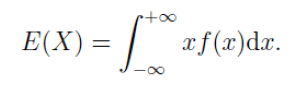
(二)、方差(Variance)
方差是各個資料與平均數之差的平方的平均數。在概率論和數理統計中,方差用來度量隨機變數和其數學期望(即均值)之間的偏離程度。
設X為隨機變數,如果E{[X-E(X)]^2}存在,則稱E{[X-E(X)]^2}為X的方差,記為Var(X)。
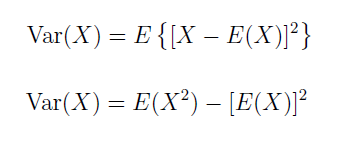
R程式:計算樣本(1,2,3,7,21)的方差
> S<-c(1,2,3,7,21)
> var(S)
[1] 68.2(三)、標準差(Standard Deviation)
標準差是方差的算術平方根sqrt(var(X))。標準差能反映一個數據集的離散程度。平均數相同的,標準差未必相同。
R程式:計算樣本(1,2,3,7,21)標準差
> S<-c(1,2,3,7,21)
> sd(S)
[1] 8.258329(四)、各種分佈的期望和方差
離散型分佈:兩點分佈,二項分佈,泊松分佈等
連續型分佈:均勻分佈,指數分佈,正態分佈,伽馬分佈等對於某一特定場景,其所符合的分佈規律一般先驗給出
(五)、常用統計量
1.眾數(Mode):
一組資料中出現次數最多的數值,叫眾數,有時眾數在一組數中有好幾個。
R程式:計算樣本(1,2,3,3,3,7,7,7,7,9,10,21)的眾數
> S<-c(1,2,3,3,3,7,7,7,7,9,10,21)
> names(which.max(table(S)))
[1] "7"
#table()的輸出可以看成是一個帶名字的數字向量。可以用names()和as.numeric()分別得到名稱和頻數
> x <- sample(c("a", "b", "c"), 100, replace=TRUE)
> names(table(x))
[1] "a" "b" "c"
> as.numeric(table(x))
[1] 42 25 33
也可以直接把輸出結果轉化為資料框,as.data.frame():
> as.data.frame(table(x))
x Freq
1 a 42
2 b 25
3 c 33
> table(S)
S
1 2 3 7 9 10 21
1 1 3 4 1 1 1 2.最小值(minimum):
在給定情形下可以達到的最小數量或最小數值
3.最大值(maximum):
在給定情形下可以達到的最大數量或最大數值
4.中位數(Medians):
是指將統計總體當中的各個變數值按大小順序排列起來,形成一個數列,處於變數數列中間位置的變數值就稱為中位數
5.四分位數(Quartile):
用於描述任何型別的資料,尤其是偏態資料的離散程度,即將全部資料從小到大排列,正好排列在上1/4位置叫上四分位數,下1/4位置上的數就叫做下四分位數
R程式:計算樣本(1,2,3,4,5,6,7,8,9)的四分位數
> S<-c(1,2,3,4,5,6,7,8,9)
> quantile(S)
0% 25% 50% 75% 100%
1 3 5 7 9
> fivenum(S)
[1] 1 3 5 7 96.通用的計算統計函式:
R程式:計算樣本(1,2,3,4,5,6,7,8,9)的統計函式
> S<-c(1,2,3,4,5,6,7,8,9)
> summary(S)
Min. 1st Qu. Median Mean 3rd Qu. Max.
1 3 5 5 7 9 (六)、協方差(Covariance)
協方差用於衡量兩個變數的總體誤差。而方差是協方差的一種特殊情況,即當兩個變數是相同的情況。設X,Y為兩個隨機變數,稱E{[X-E(X)][Y-E(Y)]}為X和Y的協方差,記錄Cov(X,Y)。
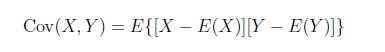
R程式:計算X(1,2,3,4)和Y(5,6,7,8)的協方差
> X<-c(1,2,3,4)
> Y<-c(5,6,7,8)
> cov(X,Y)
[1] 1.666667(七)、相關係數(Correlation coefficient)
相關係數是用以反映變數之間相關關係密切程度的統計指標。相關係數是按積差方法計算,同樣以兩變數與各自平均值的離差為基礎,通過兩個離差相乘來反映兩變數之間相關程度。當Var(X)>0, Var(Y)>0時,稱Cov(X,Y)/sqrt(Var(X)*Var(Y))為X與Y的相關係數。
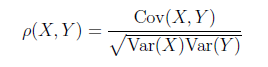
R程式:計算X(1,2,3,4)和Y(5,7,8,9)的相關係數
> X<-c(1,2,3,4)
> Y<-c(5,7,8,9)
> cor(X,Y)
[1] 0.9827076(八)、矩
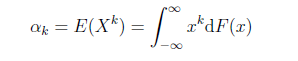
1.原點矩(moment about origin)
2.中心矩(moment about centre)
均值和方差分別就是一階原點矩和二階中心矩,具體定義和概念,可詳見陳希孺《概率論與數理統計》P132-133
3.偏度(skewness):
是統計資料分佈偏斜方向和程度的度量,是統計資料分佈非對稱程度的數字特徵。設分佈函式F(x)有中心矩μ2=E(X −E(X))^2, μ3 = E(X −E(X))^3,則Cs=μ3/μ2^(3/2)為偏度係數。
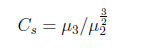
當Cs>0時,概率分佈偏向均值右則,Cs<0時,概率分佈偏向均值左則。 R語言:計算10000個正態分佈的樣本的偏度
> library(PerformanceAnalytics)
> S<-rnorm(10000)
> skewness(S)
[1] -0.00178084
> hist(S,breaks=100)
#hist() 函式:繪製直方圖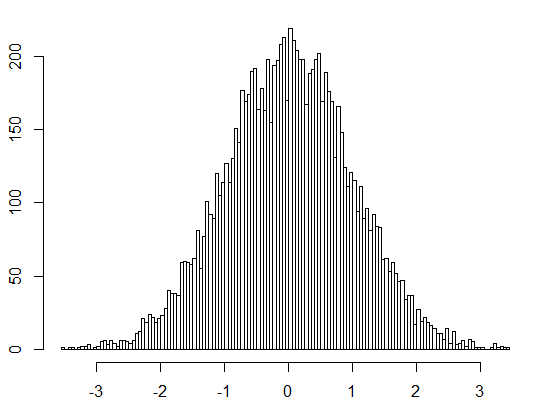
4.峰度(kurtosis): 又稱峰態係數。
表徵概率密度分佈曲線在平均值處峰值高低的特徵數。峰度刻劃不同型別的分佈的集中和分散程式。設分佈函式F(x)有中心矩μ2=E(X −E(X))^2, μ4=E(X −E(X))^4,則Ck=μ4/(u2^2-3)為峰度係數。
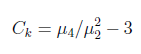
R語言:計算10000個正態分佈的樣本的峰度,(同偏度的樣本資料)
> library(PerformanceAnalytics)
> kurtosis(S)
[1] -0.02443549
> hist(S,breaks=100)(九)、協方差矩陣(covariance matrix)
可以理解成不同維度上的協方差
> x=as.data.frame(matrix(rnorm(10),ncol=2))
> x
V1 V2
1 -2.11315384 -2.55189840
2 -0.96631271 -1.36148355
3 -0.02835058 -0.82328774
4 -1.86669567 -0.07201353
5 0.27324957 -2.23835218
> var(x)
V1 V2
V1 1.13470650 -0.09292042
V2 -0.09292042 1.03172261
> cov(x)
V1 V2
V1 1.13470650 -0.09292042
V2 -0.09292042 1.03172261
三、極限定理
引言:
我們知道,隨機現象的統計性規律是在相同條件下進行大量重複試驗時呈現出來的,常見的兩種統計規律性為:
頻率的穩定性,即在大量重複試驗中,事件發生的頻率總是在它的概率附近擺動,且隨著試驗次數的增多,該頻率總是越來越明顯地穩定在其概率附近;
平均值的穩定性,即在多次重複測量中,測量平均值總是在它的真實值附近擺動,且隨著測量次數的增加,測量平均值總是越來越明顯地穩定在其真實值附近。
對以上兩種規律,人們不僅研究觀測值趨向於哪個穩定值,而且還分析了觀測值在穩定值周圍的擺動形式(分佈情況)。
針對觀測值趨向於哪個穩定值,用數學語言及理論來分析研究,就引出了大數定律。其中關於頻率穩定性的大數定律稱為伯努利大數定律,關於均值穩定性的大數定律稱為辛欽大數定律。
針對觀測值在穩定值周圍的擺動形式,用數學理論進行研究,就得出了中心極限定理.所謂的中心極限定理,就是把和的分佈收斂於正態分佈的那些定理的一個統稱。
注 在概率論中,“定律”與“定理”是一樣的意思.“定理”一般用於指那些能用數學工具嚴格證明的結論;而“定律”是指人們通過觀察分析得出來一種經驗結論,如牛頓三大定律,熱力學定律等.因為概率論中的“大數定律”不僅是在實踐中總結出來的經驗結論,而且也可以用數學工具嚴格地去證明,所以叫“大數定律”或叫“大數定理”都可以。
(一)、大數定理
R語言:假設投硬幣,正面概率是0.5,投4次時,計算得到2次正面的概率?根據大數定律,如果投是10000次,計算5000次正面的概率?
#計算2次正面的的概率
> choose(4,2)/2^4 #choose組合數的計算:從4中選擇2個
[1] 0.375
#計算5000次正面的的概率
> pbinom(5000, 10000, 0.5)
[1] 0.5039893
#pbinom二向分佈,5000為分位數,產生10000個隨機數,每個概率0.5(二)、中心極限定理(central limit theorem)
中心極限定理是概率論中的一組定理。中心極限定理說明,大量相互獨立的隨機變數,其均值的分佈以正態分佈為極限。
1.林德伯格-列維(Lindburg-Levy)
是棣莫佛-拉普拉斯定理的擴充套件,討論獨立同分布隨機變數序列的中央極限定理。它表明,獨立同分布、且數學期望和方差有限的隨機變數序列的標準化和以標準正態分佈為極限:
2.棣莫佛-拉普拉斯(de Movire - Laplace)
棣莫佛-拉普拉斯(de Moivre - Laplace)定理是中央極限定理的最初版本,討論了服從二項分佈的隨機變數序列。它指出,引數為n, p的二項分佈以nρ為均值、nρ(1-ρ)為方差的正態分佈為極限。
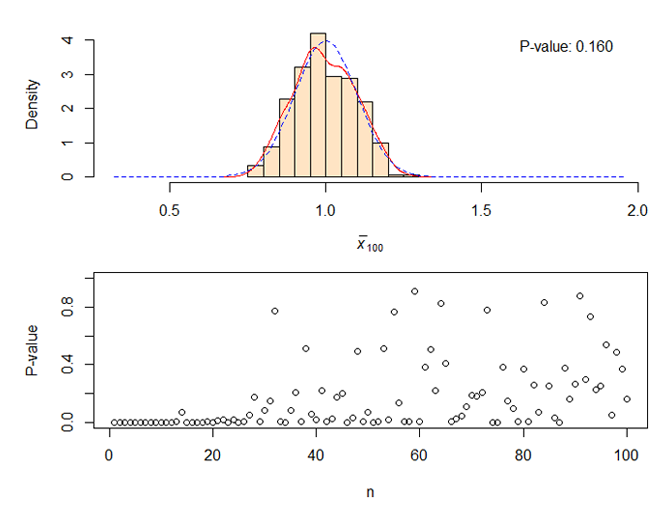
R語言:中心極限定理模擬,從指數分佈到正態分佈
if (!require(animation)) install.packages("animation")
library(animation)
ani.options(interval = 0.1, nmax = 100)
par(mar = c(4, 4, 1, 0.5))
clt.ani()
#
1.library和require都可以載入包,但二者存在區別。在一個函式中,如果一個包不存在,執行到library將會停止執行,require則會繼續執行。
require將會根據包的存在與否返回true或者false。
2.interval:a positive number to set the time interval of the animation (unit in seconds); default to be 1.
3.nmax:maximum number of steps in a loop (e.g. iterations) to create animation frames. Note: the actual number of frames can be less than this number, depending on specific animations. Default to be 50.
4.mar設定圖形空白邊界行數,mar = c(bottom, left, top, right)
5.clt.ani:Demonstration of the Central Limit Theorem
6.shapiro.test檢驗,P值大於0.05說明資料正態分佈