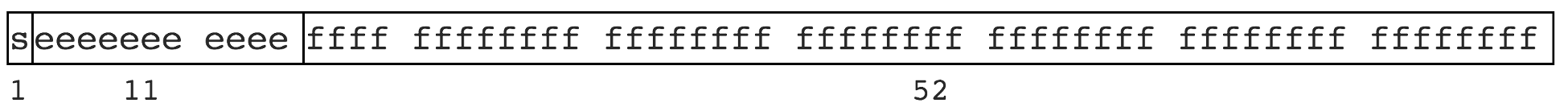由於計算機的二進位制實現和位數限制，有些數無法有限表示。就像一些無理數不能有限表示，如 圓周率 3.1415926...，1.3333... 等。JS 遵循 IEEE 754 規範，採用雙精度儲存（double precision），佔用 64 bit。

(1位用來表示符號位，11位用來表示指數，52位表示尾數）

由於無論是採用了哪種表達方式進行怎樣的計算，到了計算機的最底層，都是通過1和0的機器碼來對具體的資料和操作進行具體的實現。由於底層實現機制的原因，浮點數在轉換為二進位制表示的時候，無法精確表示這種包含小數點的資料，其本質是將浮點數轉換成了用二進位制表示的最接近的近似值。下面一個例子可以用來簡單說明浮點數在轉換為二進位制時候的計算方法

0.02625=0.000001101（二進位制），無法精確求出二進位制表示，因此採用“四捨五入法”（逢1進，逢0舍）。

以上就是問題產生的原理，很多編譯型語言如Java,c#等都對浮點數的處理進行了封裝。因此平時大多數情況下，並不會出現明顯的可見的問題。js本身作為解釋性語言，好像這點上有著天生的劣勢。

浮點數，比如

0.1 >> 0.0001 1001 1001 1001…（1001無限迴圈）
0.2 >> 0.0011 0011 0011 0011…（0011無限迴圈）

此時只能模仿十進位制進行四捨五入了，但是二進位制只有 0 和 1 兩個，於是變為 0 舍 1 入。這即是計算機中部分浮點數運算時出現誤差，丟失精度的根本原因。

大整數的精度丟失和浮點數本質上是一樣的，尾數位最大是 52 位，因此 JS 中能精準表示的最大整數是 Math.pow(2, 53)，十進位制即 9007199254740992。                                                                                                                                                              大於 9007199254740992 的可能會丟失精度

9007199254740992     >> 10000000000000...000 // 共計 53 個 0
9007199254740992 + 1 >> 10000000000000...001 // 中間 52 個 0
9007199254740992 + 2 >> 10000000000000...010 // 中間 51 個 0
9007199254740992 + 1 // 丟失        //9007199254740992 
9007199254740992 + 2 // 未丟失      //9007199254740994   
9007199254740992 + 3 // 丟失        //9007199254740992 
9007199254740992 + 4 // 未丟失      //9007199254740996   
 

JS數字精度丟失的一些典型問題

1. 兩個簡單的浮點數相加

	
0.1 + 0.2 != 0.3 // true

2. 大整數運算

9999999999999999 == 10000000000000001 // true

3. toFixed 不會四捨五入（Chrome）

1.335.toFixed(2) // 1.33

解決方案：

對於整數，前端出現問題的機率可能比較低，畢竟很少有業務需要需要用到超大整數，只要運算結果不超過 Math.pow(2, 53) 就不會丟失精度。

對於小數，前端出現問題的機率還是很多的，尤其在一些電商網站涉及到金額等資料。解決方式：把小數放到位整數（乘倍數），再縮小回原來倍數（除倍數）

// 0.1 + 0.2
(0.1*10 + 0.2*10) / 10 == 0.3 // true

toFixed的修復如下

// toFixed 修復
function toFixed(num, s) {
    var times = Math.pow(10, s)
    var des = num * times + 0.5
    des = parseInt(des, 10) / times
    return des + ''
}