2. 程式人生 > >二叉樹線索化

二叉樹線索化

阿新 • • 發佈：2019-02-05

1 原理分析
線索化意義：
二叉樹是非線性結構，遍歷二叉樹都是通過遞迴或者用棧輔助非遞迴來遍歷的。
1）不借用棧或者佇列來實現遍歷的非遞迴，還有一種方法是線索化。
2）為了實現迭代器，面向物件。
如果我們知道一個節點的前驅和後繼，那麼我們就可直接遍歷二叉樹。
設定二叉樹節點的前驅和後繼，就是線索化二叉樹，我們利用指向左右子樹的空指標存放節點的前驅和後繼。
線索化設計思路：
遍歷二叉樹，當遍歷到一個節點的左節點或右節點為空時，設定它的前驅和後繼，那麼訪問時直接可根據節點的前驅和後繼來進行訪問
1.1 中序線索化和遍歷
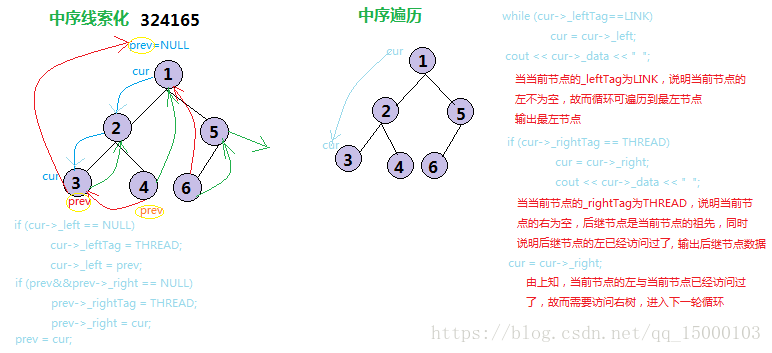
這裡寫圖片描述
1.2 前序線索化和遍歷
這裡寫圖片描述
1.3 後續線索化和遍歷


這裡寫圖片描述
2 程式碼實現：

//BinaryTreeNodeThd.h
#pragma once
#include<iostream>
#include<string.h>
#include<assert.h>

enum PointerTag { THREAD, LINK };

template<class T>
struct BinaryTreeNodeThd
{
    T _data; // 資料
    BinaryTreeNodeThd* _left; // 左孩子
    BinaryTreeNodeThd* _right; // 右孩子
    PointerTag _leftTag; // 左孩子線索標誌
 

    PointerTag _rightTag; // 右孩子線索標誌
    BinaryTreeNodeThd* _parent;//用於後序遍歷

    BinaryTreeNodeThd(const T& d)
        :_data(d)
        , _left(NULL)
        , _right(NULL)
        , _leftTag(LINK)
        , _rightTag(LINK)
        , _parent(NULL)
    {}
};

// 基類迭代器
template<class T>
struct __BinaryTreeIterator
{
    typedef BinaryTreeNodeThd<
 
T> Node;
    typedef __BinaryTreeIterator<T> Self;
    Node* _node;
    __BinaryTreeIterator(Node* node)
        :_node(node)
    {}
    T& operator *()
    {
        return _node->_data;
    }
    T* operator ->()
    {
        return &(operator *());
    }
    bool operator =(const Self& s)
    {
        return _node == s._node;
    }
    bool operator !=(const Self& s)
    {
        return _node != s._node;
    }
    virtual Self& operator++()=0;
};


template<class T>
struct __BinaryTreeInIterator : public __BinaryTreeIterator<T>//中序迭代器
{
    typedef BinaryTreeNodeThd<T> Node;
    typedef __BinaryTreeInIterator<T> Self;
    __BinaryTreeInIterator(Node* node)
        :__BinaryTreeIterator(node)
    {   }
    Self& operator++()
    {
        if (_node->_rightTag == THREAD)
        {
            _node = _node->_right;
        }
        else
        {
            _node = _node->_right;
            while (_node->_leftTag == LINK)
            {
                _node = _node->_left;
            }
        }
        return *this;
    }
};

template<class T>
struct __BinaryTreePrevIterator : public __BinaryTreeIterator<T>//前序迭代器
{
    typedef BinaryTreeNodeThd<T> Node;
    typedef __BinaryTreePrevIterator<T> Self;
    __BinaryTreePrevIterator(Node* node)
        :__BinaryTreeIterator(node)
    {}
    Self& operator ++ ()
    {
        if (_node->_rightTag == LINK)
        {
            _node = _node->_left;
        }
        else
        {
            _node = _node->_right;
        }
        return *this;
    }
};


template<class T>
struct BinaryTreeThd
{
public:
    typedef BinaryTreeNodeThd<T> Node;
    typedef __BinaryTreeIterator<T> Iterator;
    typedef __BinaryTreeInIterator<T> InIterator;
    typedef __BinaryTreePrevIterator<T> PrevIterator;

    BinaryTreeThd(T* a, size_t n, const T& invalid)
        :_root(NULL)
    {
        size_t index = 0;
        Node* parent = NULL;
        _root = _CreatTree(a, n, index, invalid,parent);
    }

    InIterator InBegin()
    {
        Node* cur = _root;
        while (cur&&cur->_leftTag==LINK)
        {
            cur = cur->_left;
        }
        return cur;
    }
    InIterator InEnd()
    {
        return NULL;
    }

    PrevIterator PrevBegin()
    {
        return _root;
    }
    PrevIterator PrevEnd()
    {
        return NULL;
    }

    void _InOrderThreading(Node* cur, Node*& prev)
    {
        if (cur == NULL)
        {
            return;
        }
        _InOrderThreading(cur->_left, prev);
        if (cur->_left == NULL)//當cur左為空時，線索化cur左
        {
            cur->_leftTag = THREAD;
            cur->_left = prev;
        }
        if (prev&&prev->_right == NULL)//當prev右為空時，線索化prev右
        {
            prev->_rightTag = THREAD;
            prev->_right = cur;
        }
        prev = cur;
        _InOrderThreading(cur->_right, prev);
    }
    // 中序線索化
    void InOrderThreading()
    {
        Node* prev = NULL;
        _InOrderThreading(_root, prev);
        prev->_rightTag = THREAD;
    }

    void _PrevThreading(Node* cur, Node*& prev)
    {
        if (cur == NULL)
        {
            return;
        }
        if (cur->_left == NULL)
        {
            cur->_leftTag = THREAD;
            cur->_left = prev;
        }
        if (prev&&prev->_right == NULL)
        {
            prev->_rightTag = THREAD;
            prev->_right = cur;
        }
        prev = cur;
        if (cur->_leftTag == LINK)
        {
            _PrevThreading(cur->_left, prev);
        }
        if (cur->_rightTag == LINK)
        {
            _PrevThreading(cur->_right, prev);
        }
    }

    // 前序線索化
    void PrevThreading()
    {
        Node* prev = NULL;
        _PrevThreading(_root, prev);
        prev->_rightTag = THREAD;
    }

    void _PostOrderThreading(Node* cur, Node*& prev)
    {
        if (cur == NULL)
        {
            return;
        }
        _PostOrderThreading(cur->_left, prev);
        _PostOrderThreading(cur->_right, prev);
        if (cur->_left == NULL)
        {
            cur->_leftTag = THREAD;
            cur->_left = prev;
        }
        if (prev&&prev->_right == NULL)
        {
            prev->_rightTag = THREAD;
            prev->_right = cur;
        }
        prev = cur;
    }
    // 後序線索化
    void PostOrderThreading()
    {
        Node* prev = NULL;
        _PostOrderThreading(_root, prev);
    }

    void InOrderThd()//中序遍歷
    {
        Node* cur = _root;
        while (cur)
        {
            while (cur->_leftTag==LINK)
            {
                cur = cur->_left;
            }
            cout << cur->_data << "  ";
            if (cur->_rightTag == THREAD)
            {
                cur = cur->_right;
                cout << cur->_data << "  ";
            }
            cur = cur->_right;
        }
        cout << endl;
    }

    void PrevOrderThd()//先序遍歷
    {
        Node* cur = _root;
        while (cur)
        {
            while (cur->_leftTag == LINK)
            {
                cout << cur->_data << "  ";
                cur = cur->_left;
            }
            cout << cur->_data << "  ";
            cur = cur->_right;
        }
        cout << endl;
    }

    void PostOrderThd()//後序遍歷
    {
        Node* cur = _root;
        Node*prev = NULL;
        while (cur)
        {
            //第一步：找樹最左邊的節點  
            while (cur->_left!=prev&&cur->_leftTag == LINK)
            {
                cur = cur->_left;
            }   
            //第二步：訪問後繼
            while (cur&&cur->_rightTag == THREAD)
            {
                cout << cur->_data << "  ";
                prev = cur;
                cur = cur->_right;
            }
            //判斷此時cur是不是指向了根節點 
            if (cur == _root)
            {
                cout << cur->_data << "  ";
                return;
            }
            while (cur!=NULL&&cur->_right == prev)
            {
                cout << cur->_data << "  ";
                prev = cur;
                cur = cur->_parent;//往上一級走 
            }
            if (cur&&cur->_rightTag == LINK)
            {
                cur = cur->_right;
            }
        }
        cout << endl;
    }

protected:
    Node* _CreatTree(const T *a, size_t size, size_t &index, const T& invalid,Node*& parent)//建立二叉樹
    {
        assert(a);
        Node* node = NULL;
        if (a[index] != invalid&&index < size)
        {
            node = new Node(a[index]);
            node->_parent = parent;
            node->_left = _CreatTree(a, size, ++index, invalid,node);
            node->_right = _CreatTree(a, size, ++index, invalid,node);
        }
        return node;
    }   
private:
    Node* _root;
};

 //簡單模式
void TestBinaryTreeThd1()
{
 int a1[] = {1, 2, 3, '#', '#', 4, '#' , '#', 5, 6};
 BinaryTreeThd<int> t1(a1, sizeof(a1)/sizeof(a1[0]), '#');
 t1.InOrderThreading();
 t1.InOrderThd();

 BinaryTreeThd<int>::InIterator it1 = t1.InBegin();
 while(it1 != t1.InEnd())
 {
      cout<<*it1<<"  ";
      ++it1;
 }
 cout <<endl;

 BinaryTreeThd<int> t2(a1, sizeof(a1) / sizeof(a1[0]), '#');
 t2.PrevThreading();

 BinaryTreeThd<int>::PrevIterator it2 = t2.PrevBegin();
 while(it2 != t2.PrevEnd())
 {
 cout<<*it2<<"  ";
 ++it2;
 }
 cout << endl;
}

// 繼承加多型
void TestBinaryTreeThd2()
{
    int a1[] = { 1, 2, 3, '#', '#', 4, '#', '#', 5, 6 };
    BinaryTreeThd<int> t1(a1, sizeof(a1) / sizeof(a1[0]), '#');
    t1.InOrderThreading();
    t1.InOrderThd();

    BinaryTreeThd<int>::Iterator& it1 = t1.InBegin();
    while (it1 != t1.InEnd())
    {
        cout << *it1 << "  ";
        ++it1; // 多型
    }
    cout << endl;

    BinaryTreeThd<int> t2(a1, sizeof(a1) / sizeof(a1[0]), '#');
    t2.PrevThreading();

    BinaryTreeThd<int>::Iterator& it2 = t2.PrevBegin();
    while (it2 != t2.PrevEnd())
    {
        cout << *it2 << "  ";
        ++it2;
    }
    cout << endl;
}
//test.cpp
using namespace std;
#include"BinaryTreeNodeThd.h"
#include"assert.h"

void TestBinaryTreeThd()
{
    int array[] = { 1, 2, 3, '#', '#', 4, '#', '#', 5, 6, '#', '#', '#' };
    BinaryTreeThd<int> t(array,13, '#');
    t.InOrderThreading();
    t.InOrderThd();

    BinaryTreeThd<int> t1(array, 13, '#');
    t1.PrevThreading();
    t1.PrevOrderThd();

    BinaryTreeThd<int> t2(array, 13, '#');
    t2.PostOrderThreading();
    t2.PostOrderThd();
}
int main()
{
    TestBinaryTreeThd();
    cout << endl << "***********************************************************" << endl;
    TestBinaryTreeThd1();
    cout << endl << "***********************************************************" << endl;
    TestBinaryTreeThd2();
    system("pause");
    return 0;
}

測試執行結果：
這裡寫圖片描述

相關推薦

線索二叉樹--二叉樹線索化

type 兩個 標記 typedef 指針 有一個 進行 查找 後繼節點 遍歷二叉樹是對非線性結構進行線性化操作，在得到的訪問序列中，每個節點都只有一個直接前去和一個直接後繼。 引入線索二叉樹可以加快查找前去於後繼節點的速度，實質就是將二叉鏈表中的空指針改為指向前驅或者後繼

二叉樹線索化和遍歷的演算法

前言： 關於二叉線索樹有什麼作用，為什麼要建立這裡就不介紹。因為時間問題，只是總結一下線索化和遍歷的演算法。這個演算法和前面總結過的非遞迴法遍歷二叉樹都算是資料結構裡面難度係數比棧，佇列，線性表那些大的演算法。限定時間內要寫出來還是有些難度，最好是能有所總結，

二叉樹線索化以及線索化的先序、中序、後序遍歷

本篇部落格主要講述：二叉樹的線索化以及對線索二叉樹遍歷實現。 首先，什麼是二叉樹的線索化，為什麼要對二叉樹線索化？ 二叉樹是一種非線性結構，遍歷二叉樹幾乎都是通過遞迴或者用棧輔助實現非遞迴的遍歷。用二叉樹作為儲存結構時，取到一個節點，只能獲取節點的左孩子和右孩子，不能直

二叉樹線索化

1 原理分析 線索化意義： 二叉樹是非線性結構，遍歷二叉樹都是通過遞迴或者用棧輔助非遞迴來遍歷的。 1）不借用棧或者佇列來實現遍歷的非遞迴，還有一種方法是線索化。 2）為了實現迭代器，面向物件。 如果我們知道一個節點的前驅和後繼，那麼我們就可直接遍歷

二叉樹序列化/反序列化

二叉樹被記錄成檔案的過程，為二叉樹的序列化 通過檔案重新建立原來的二叉樹的過程，為二叉樹的反序列化 設計方案並實現。 （已知結點型別為32位整型）   思路：先序遍歷實現。 因為要寫入檔案，我們要把二叉樹序列化為一個字串。 首先，我們要規定，一個結點結束後的

前端fabric.js實現二叉樹視覺化佈局

2.效果圖 3.程式碼 <!DOCTYPE html> <html> <head> <meta http-equiv="Content-Type" content="text/html; charset=utf-8" />

劍指_二叉樹序列化與反序列化

題目：首先我們介紹二叉樹先序序列化的方式，假設序列化的結果字串為str，初始時str等於空字串。先序遍歷二叉樹，如果遇到空節點，就在str的末尾加上“#!”，“#”表示這個節點為空，節點值不存在，當然你也可以用其他的特殊字元，“!”表示一個值的結束。如果遇到不為空的節點，假設節點值為3，就在str的

二叉樹的線索化

chan 構建 訪問 線索二叉樹 borde class 序列 oot png 二叉樹是一種非線性結構，遍歷二叉樹幾乎都是通過遞歸或者用棧輔助實現非遞歸的遍歷。二叉樹作為存儲結構時，一個節點只能獲取節點的左孩子和右孩子，不能直接得到節點的任一遍歷序列的前驅或者後繼。為了保存

為什麽二叉樹總能中序線索化

思想 計算 編程 中序遍歷 發揮 合成 會有 二叉線索樹 整體 為什麽二叉樹為什麽總是可以按照中序遍歷線索化空指針是夠但怎麽保證不會有一個有左右孩子的節點不被別人指到想了想可以用類似於數學歸納法這樣證明： 先討論三種最簡單的情形 1. ab c b左指針

二叉樹的線索化(摘自天勤資料結構高分筆記)

/************************************************************************/ /*      二叉樹的線索化：二叉樹的線索化可以將二叉樹非遞迴遍歷演算法中的使用者棧也給省掉，進一步提高效率     中序線

二叉樹的線索化演算法思想詳解

    二叉樹的線索化，這幾天以來我很難掌握，今天終於想通了，哈哈，首先我們來看看二叉樹線索化之後會變成什麼樣子，這裡我們以圖中的二叉樹為例，圖如下：    畫的太糙，各位看官講究著看吧- -。所謂二叉樹的線索化，就是當一個節點的左右指標為空時，就讓它的左右指標指向該節點的前

【c++】二叉樹的線索化

什麼是二叉樹的線索化？或者問什麼是線索二叉樹？ 按照某種遍歷方式對二叉樹進行遍歷，可以把二叉樹中所有結點排序為一個線性序列。在改序列中，除第一個結點外每個結點有且僅有一個直接前驅結點；除最後一個結點外

線索二叉樹和中序非遞迴遍歷線索化後的二叉樹

//線索二叉樹 #include<stdio.h> #include<malloc.h> #include<process.h> #define OVERFLOW -2 //二叉樹的二叉線索儲存結構 enum PointerTag{Lin

二叉樹的線索化及其前驅後繼查詢

一 實質 遍歷二叉樹過程中用線索（前驅和後繼）取代空指標的的做法 二 演算法分析（給出中序化）： 主要是增加倆個指標，pre指標始終指向剛剛訪問過的節點，p指標始終指向當前訪問的節點其中，*pre是*p的前驅，*p是*pre的後繼 三 中序線索化演算法： //將二叉樹按

中序線索二叉樹的建立、線索化和遍歷（前序遍歷和後序遍歷）

線索二叉樹的概念 線索二叉樹的原理：線索二叉樹是將普通二叉樹左右孩子中的空鏈域利用起來，將左孩子空鏈域指向當前節點的線性遍歷前驅，將右孩子空鏈域指向當前節點的線性遍歷後繼，指向該線性序列中的前驅或後繼

線索二叉樹（中序線索化、遍歷、查詢後序的前驅、查詢前驅的後繼）

#include <stdio.h> #include <stdlib.h> typedef struct ThreadNode{ char data; struct ThreadNode *lchild,*rchild ; int ltag

線索二叉樹原理及前序、中序線索化（Java版）

轉載原文地址：https://blog.csdn.net/UncleMing5371/article/details/54176252一、線索二叉樹原理      前面介紹二叉樹原理及特殊二叉樹文章中提到，二叉樹可以使用兩種儲存結構：順序儲存和二叉連結串列。在使用二叉連結串列

C語言：線索二叉樹的線索化及其遍歷實現

       前序和中序遍歷都實現了，後序線索化還不是很明白！如有大神看到，望指正！不勝感激！ // 中序線索二叉樹實現.cpp : 定義控制檯應用程式的入口點。 // #include "stdafx.h" #include<iostream> #includ

線索二叉樹的構建和遍歷------小甲魚數據結構和算法

-- tag typedef pre == 約定 cnblogs amp scan #include <stdio.h> #include <stdlib.h> typedef char ElemType; // 線索存儲標誌位 // Link

二叉樹的序列化和反序列化

nbsp node 使用遞歸 輸入 特殊字符 this tail 改變 代碼實現 http://blog.csdn.net/qq_27703417/article/details/70958692 先序遍歷二叉樹，如果遇到空節點，就在str的末尾加上“#!”，“#”表示