一致性問題可以算是分散式領域的一個聖殿級問題了，關於它的研究可以回溯到幾十年前。

拜占庭將軍問題

Leslie Lamport 在三十多年前發表的論文《拜占庭將軍問題》（參考[1]）。

拜占庭位於如今的土耳其的伊斯坦布林，是東羅馬帝國的首都。由於當時拜占庭羅馬帝國國土遼闊，為了防禦目的，因此每個軍隊都分隔很遠，將軍與將軍之間只能靠信差傳訊息。在戰爭的時候，拜占庭軍隊內所有將軍必需達成 一致的共識，決定是否有贏的機會才去攻打敵人的陣營。但是，在軍隊內有可能存有叛徒和敵軍的間諜，左右將軍們的決定又擾亂整體軍隊的秩序，在進行共識時，結果並不代表大多數人的意見。這時候，在已知有成員不可靠的情況下，其餘忠誠的將軍在不受叛徒或間諜的影響下如何達成一致的協議，拜占庭問題就此形成。拜占庭假設是對現實世界的模型化，由於硬體錯誤、網路擁塞或斷開以及遭到惡意攻擊，計算機和網路可能出現不可預料的行為。

Lamport 一直研究這類問題，發表了一系列論文。但綜合總結一下就是回答下面三個問題：

1. 類似拜占庭將軍這樣的分散式一致性問題是否有解？
2. 如果有解的話需要滿足什麼樣的條件？
3. 在特定前提條件的基礎上，提出一種解法。

前兩個問題 Lamport 在論文《拜占庭將軍問題》已經回答，而第三個問題在後來的論文 《The Part-Time Parliament》中提出了一種演算法並命名為 Paxos。這篇論文使用了大量的數學證明，而我基本就看不懂了（數學符號都認不全-｡-;），考慮到大家理解起來都比較困難，後來 Lamport 又寫了另外一篇論文 《Paxos Made Simple》完全放棄了所有數學符號的證明，使用純英文的邏輯推導。我勉強逐字看了一遍，然後感覺若有所悟，但你問我搞懂了嗎，我的標準應該還是沒懂。對我來說理解一個演算法有個明確的標準，就是真的懂了會在頭腦裡能將演算法對映為程式碼，而看完後面一篇論文僅僅是若有所悟還達不到能對映為程式碼的清晰度。

雖然 Lamport 認為 Paxos 很 simple，但也許只是針對他的頭腦而言。事實是大家理解起來都還是很困難，所以 Raft 就是建立在希望得到一個更易於理解的 Paxos 演算法的替代品。把可理解性作為演算法的主要目標之一，從論文題目就可看出來《In Search of an Understandable Consensus Algorithm》。

在進入正題前，我想起一箇舊故事可以很直觀的感受對一個問題不同的思維視角在可理解性上的差異。

不同視角的可理解性

依稀記得大約在二十年前，我還在讀初中時在一本可能大概叫《數學中的發散思維》（不能很清晰記得書名了）的書中看到這麼一個有趣的問題。

甲乙兩人輪流在一張圓桌上平放黑白圍棋子，每次放一子，棋子不許重疊，誰先沒有地方放就輸。
請問怎樣放才能贏？

這個問題有兩層意思，第一，有沒有一種放法保證必贏？第二，如果有怎麼證明？這裡先停頓下，思考十秒鐘。

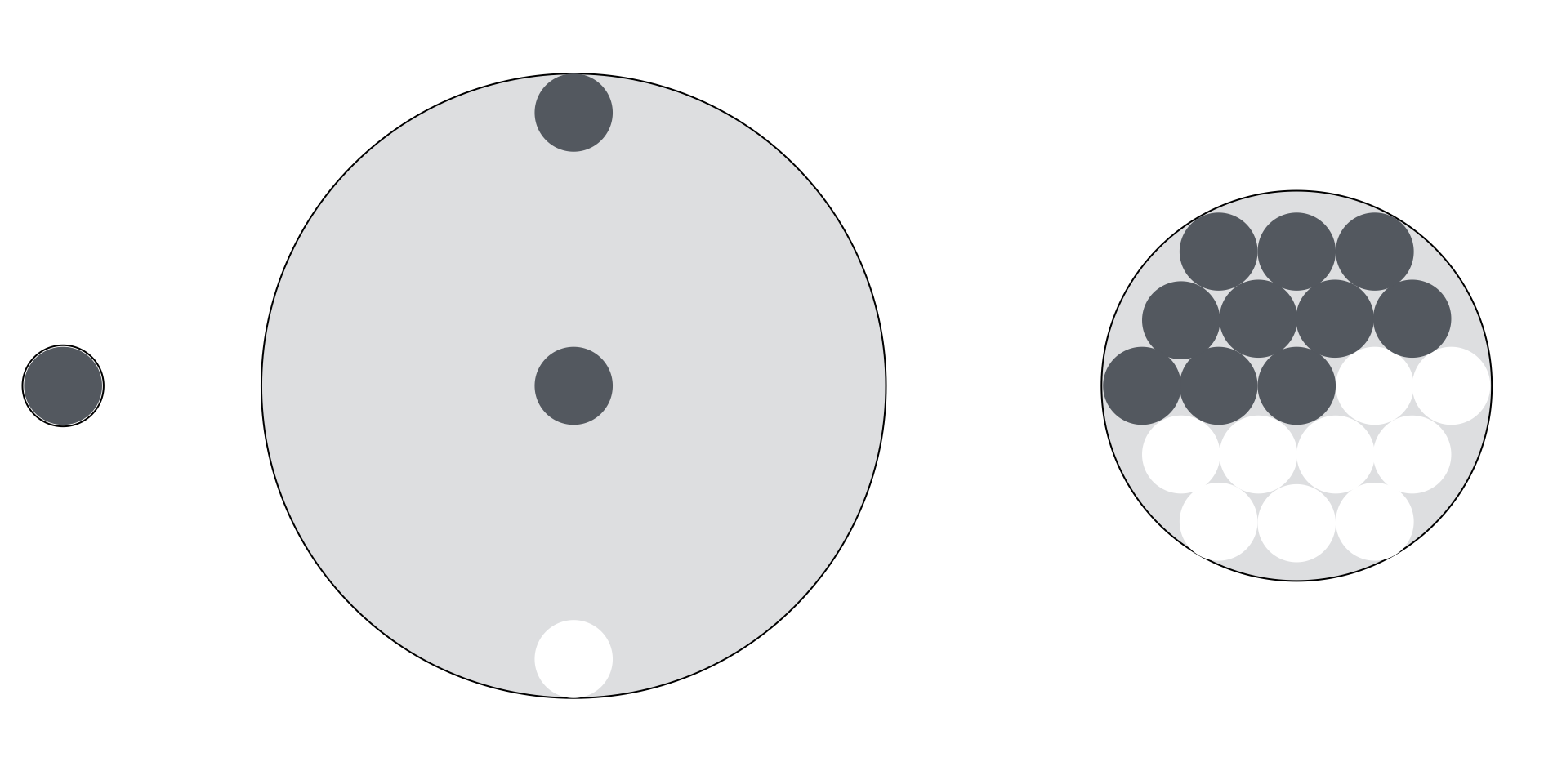
上面的圖回答了這個問題，就是先行者必勝，這裡使用了三種不同的思維方式。

1. 假如桌子只有一個圍棋子那麼大。
2. 假如桌子無限大，先行者先佔住圓心，由於圓是對稱圖形，所以只要對手還能找到位置放，你總能在對稱的另一面找到位置放。
3. 一個圓中可畫單數個直徑相等且互切的小圓。

三種不同的思維方式在可理解性難度上逐漸加深。第一種是極簡化思維，但數學上是不嚴謹的。第二種是極限思維，和第一種結合起來就是數學歸納法了，在數學上是嚴謹的。第三種是形象思維，使用了幾何學概念，但對於沒有幾何學基礎知識的人就很難理解了。

Raft 協議的易理解性描述

雖然 Raft 的論文比 Paxos 簡單版論文還容易讀了，但論文依然發散的比較多，相對冗長。讀完後掩卷沉思覺得還是整理一下才會更牢靠，變成真正屬於自己的。這裡我就藉助前面黑白棋落子裡第一種極簡思維來描述和概念驗證下 Raft 協議的工作方式。

在一個由 Raft 協議組織的叢集中有三類角色：

1. Leader（領袖）
2. Follower（群眾）
3. Candidate（候選人）

就像一個民主社會，領袖由民眾投票選出。剛開始沒有領袖，所有叢集中的參與者都是群眾，那麼首先開啟一輪大選，在大選期間所有群眾都能參與競選，這時所有群眾的角色就變成了候選人，民主投票選出領袖後就開始了這屆領袖的任期，然後選舉結束，所有除領袖的候選人又變回群眾角色服從領袖領導。這裡提到一個概念「任期」，用術語 Term 表達。關於 Raft 協議的核心概念和術語就這麼多而且和現實民主制度非常匹配，所以很容易理解。三類角色的變遷圖如下，結合後面的選舉過程來看很容易理解。

Leader 選舉過程

在極簡的思維下，一個最小的 Raft 民主叢集需要三個參與者（如下圖：A、B、C），這樣才可能投出多數票。初始狀態 ABC 都是 Follower，然後發起選舉這時有三種可能情形發生。下圖中前二種都能選出 Leader，第三種則表明本輪投票無效（Split Votes），每方都投給了自己，結果沒有任何一方獲得多數票。之後每個參與方隨機休息一陣（Election Timeout）重新發起投票直到一方獲得多數票。這裡的關鍵就是隨機 timeout，最先從 timeout 中恢復發起投票的一方向還在 timeout 中的另外兩方請求投票，這時它們就只能投給對方了，很快達成一致。

選出 Leader 後，Leader 通過定期向所有 Follower 傳送心跳資訊維持其統治。若 Follower 一段時間未收到 Leader 的心跳則認為 Leader 可能已經掛了再次發起選主過程。

Leader 節點對一致性的影響

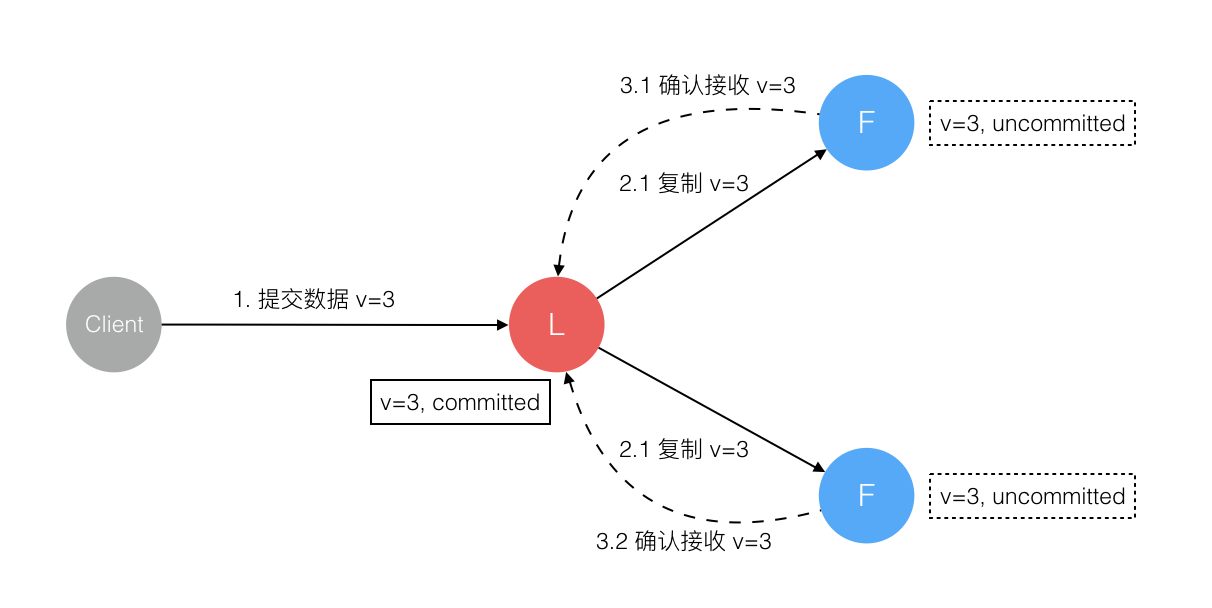
Raft 協議強依賴 Leader 節點的可用性來確保叢集資料的一致性。資料的流向只能從 Leader 節點向 Follower 節點轉移。當 Client 向叢集 Leader 節點提交資料後，Leader 節點接收到的資料處於未提交狀態（Uncommitted），接著 Leader 節點會併發向所有 Follower 節點複製資料並等待接收響應，確保至少叢集中超過半數節點已接收到資料後再向 Client 確認資料已接收。一旦向 Client 發出資料接收 Ack 響應後，表明此時資料狀態進入已提交（Committed），Leader 節點再向 Follower 節點發通知告知該資料狀態已提交。

在這個過程中，主節點可能在任意階段掛掉，看下 Raft 協議如何針對不同階段保障資料一致性的。

1. 資料到達 Leader 節點前

這個階段 Leader 掛掉不影響一致性，不多說。

2. 資料到達 Leader 節點，但未複製到 Follower 節點

這個階段 Leader 掛掉，資料屬於未提交狀態，Client 不會收到 Ack 會認為超時失敗可安全發起重試。Follower 節點上沒有該資料，重新選主後 Client 重試重新提交可成功。原來的 Leader 節點恢復後作為 Follower 加入叢集重新從當前任期的新 Leader 處同步資料，強制保持和 Leader 資料一致。

3. 資料到達 Leader 節點，成功複製到 Follower 所有節點，但還未向 Leader 響應接收

這個階段 Leader 掛掉，雖然資料在 Follower 節點處於未提交狀態（Uncommitted）但保持一致，重新選出 Leader 後可完成資料提交，此時 Client 由於不知到底提交成功沒有，可重試提交。針對這種情況 Raft 要求 RPC 請求實現冪等性，也就是要實現內部去重機制。

4. 資料到達 Leader 節點，成功複製到 Follower 部分節點，但還未向 Leader 響應接收

這個階段 Leader 掛掉，資料在 Follower 節點處於未提交狀態（Uncommitted）且不一致，Raft 協議要求投票只能投給擁有最新資料的節點。所以擁有最新資料的節點會被選為 Leader 再強制同步資料到 Follower，資料不會丟失並最終一致。

5. 資料到達 Leader 節點，成功複製到 Follower 所有或多數節點，資料在 Leader 處於已提交狀態，但在 Follower 處於未提交狀態

這個階段 Leader 掛掉，重新選出新 Leader 後的處理流程和階段 3 一樣。

6. 資料到達 Leader 節點，成功複製到 Follower 所有或多數節點，資料在所有節點都處於已提交狀態，但還未響應 Client

這個階段 Leader 掛掉，Cluster 內部資料其實已經是一致的，Client 重複重試基於冪等策略對一致性無影響。

7. 網路分割槽導致的腦裂情況，出現雙 Leader

網路分割槽將原先的 Leader 節點和 Follower 節點分隔開，Follower 收不到 Leader 的心跳將發起選舉產生新的 Leader。這時就產生了雙 Leader，原先的 Leader 獨自在一個區，向它提交資料不可能複製到多數節點所以永遠提交不成功。向新的 Leader 提交資料可以提交成功，網路恢復後舊的 Leader 發現叢集中有更新任期（Term）的新 Leader 則自動降級為 Follower 並從新 Leader 處同步資料達成叢集資料一致。

綜上窮舉分析了最小叢集（3 節點）面臨的所有情況，可以看出 Raft 協議都能很好的應對一致性問題，並且很容易理解。