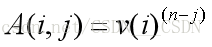【MATLAB】幾種特殊矩陣,Hilbert矩陣,Toeplitz矩陣,Vandermonde矩陣......
1、Hadamard矩陣
Hadamard矩陣是由+1和-1元素構成的且滿足Hn*Hn’=nI(這裡Hn’為Hn的轉置,I為單位方陣)n階方陣。
>> hadamard(4)
ans =
1 1 1 1
1 -1 1 -1
1 1 -1 -1
1 -1 -1 12、Hankel矩陣:是指每一條副對角線上的元素都相等的方陣。
>> x=[1 2 3 4 5 6 7] x = 1 2 3 4 5 6 7 >> hankel(x) ans = 1 2 3 4 5 6 7 2 3 4 5 6 7 0 3 4 5 6 7 0 0 4 5 6 7 0 0 0 5 6 7 0 0 0 0 6 7 0 0 0 0 0 7 0 0 0 0 0 0
hankel(x,y):
返回一個m x n的Hankel矩陣,它的第一列向量為x,最後一行為向量y
>> x=[1 2 3 4 5 6 7] x = 1 2 3 4 5 6 7 >> y=[7 6 5 4 3 2 2] y = 7 6 5 4 3 2 2 >> hankel(x,y) ans = 1 2 3 4 5 6 7 2 3 4 5 6 7 6 3 4 5 6 7 6 5 4 5 6 7 6 5 4 5 6 7 6 5 4 3 6 7 6 5 4 3 2 7 6 5 4 3 2 2
3、Pascal矩陣:
Pascal矩陣的第一行元素和第一列元素都為1,其餘位置處的元素是該元素的左邊元素加起上一行對應位置相加而得,如元素Ai,j=Ai,j-1+Ai-1,j。Ai,j表示第i行,第j列位置上的元素
>> pascal(4) ans = 1 1 1 1 1 2 3 4 1 3 6 10 1 4 10 20 >> pascal(5) ans = 1 1 1 1 1 1 2 3 4 5 1 3 6 10 15 1 4 10 20 35 1 5 15 35 70
4、Rosser矩陣
>> rosser
ans =
611 196 -192 407 -8 -52 -49 29
196 899 113 -192 -71 -43 -8 -44
-192 113 899 196 61 49 8 52
407 -192 196 611 8 44 59 -23
-8 -71 61 8 411 -599 208 208
-52 -43 49 44 -599 411 208 208
-49 -8 8 59 208 208 99 -911
29 -44 52 -23 208 208 -911 995、Wilkinson矩陣:Wilkinson特徵值測試矩陣
>> wilkinson(3)
ans =
1 1 0
1 0 1
0 1 1
>> wilkinson(5)
ans =
2 1 0 0 0
1 1 1 0 0
0 1 0 1 0
0 0 1 1 1
0 0 0 1 26、Hilbert矩陣
也成為H陣,其元素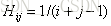
hilb(n):用於生成n x n的Hilbert矩陣
invhilb(n):用於生成n x n的Hilbert矩陣的逆矩陣整數矩陣。
>> a=hilb(3)
a =
1.0000 0.5000 0.3333
0.5000 0.3333 0.2500
0.3333 0.2500 0.2000
>> b=invhilb(3)
b =
9 -36 30
-36 192 -180
30 -180 180可以看出Hilbert矩陣和他的逆矩陣都是對稱矩陣。
7、Toeplitz矩陣
他由兩個向量定義,一個行向量和一個列向量。對稱的Toeplitz矩陣由單一向量來定義。
toeplizt(k,r):用於生成非對稱Toeplitz矩陣,第一列為k,第一行為r,其餘元素等於其左上角元素
toeplitz(c):向量c生成一個對稱的Toeplitz矩陣
>> toeplitz(2:4,2:2:8)
ans =
2 4 6 8
3 2 4 6
4 3 2 4
>> toeplitz(2:8)
ans =
2 3 4 5 6 7 8
3 2 3 4 5 6 7
4 3 2 3 4 5 6
5 4 3 2 3 4 5
6 5 4 3 2 3 4
7 6 5 4 3 2 3
8 7 6 5 4 3 28、0~1間均勻分佈的隨機矩陣
r=rand(n):產生nxn的0~1間均勻分佈的隨機矩陣
r=rand(m,n):產生mxn的0~1間均勻分佈的隨機矩陣,r=rand(m,n,p.....):與前者類似、
r=rand(size(A)):產生與A相同的0~1間均勻分佈矩陣
>> r=rand(3)
r =
0.7094 0.6797 0.1190
0.7547 0.6551 0.4984
0.2760 0.1626 0.9597
>> r=rand(3,4)
r =
0.3404 0.7513 0.6991 0.5472
0.5853 0.2551 0.8909 0.1386
0.2238 0.5060 0.9593 0.1493
>> a=[1 2;3 4]
a =
1 2
3 4
>> r=rand(size(a))
r =
0.2575 0.2543
0.8407 0.81439、標準正態分佈隨機矩陣
常用randn()函式產生均值為零、方差為1的隨機矩陣
呼叫方式如下:
r=rand(n)
r=rand(m,n)
r=rand(size(A))
r=randn([m,n,......])
>> b=randn(3)
b =
-0.1924 -1.4023 -0.1774
0.8886 -1.4224 -0.1961
-0.7648 0.4882 1.4193
>> b=randn(3,4)
b =
0.2916 -0.8045 -0.2437 -1.1480
0.1978 0.6966 0.2157 0.1049
1.5877 0.8351 -1.1658 0.7223
>> b=randn([3,4])
b =
2.5855 -0.0825 -1.7947 0.1001
-0.6669 -1.9330 0.8404 -0.5445
0.1873 -0.4390 -0.8880 0.303510、Vandermonde矩陣
A=vander(V):生成Vandermonde矩陣,矩陣的列是向量v的冪,
>> vander([1 2 3 4])
ans =
1 1 1 1
8 4 2 1
27 9 3 1
64 16 4 1
>> vander([1 ;2 ;3 ;4])
ans =
1 1 1 1
8 4 2 1
27 9 3 1
64 16 4 111、魔方矩陣:每行,每列,兩對角線上的元素和相等
>> a=magic(5)
a =
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9