圖解過程：原圖如下                                               邊集陣列按權值順序排列

           

                

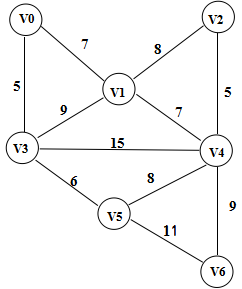
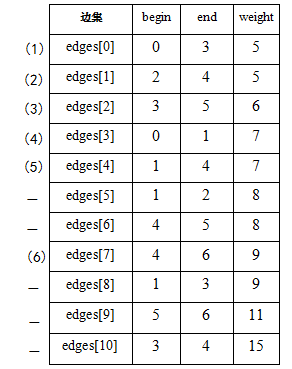
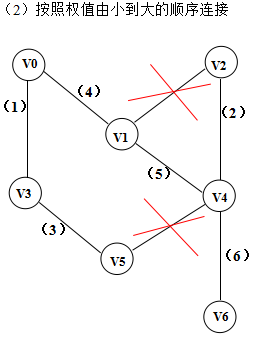
邊<1, 2>和<4, 5>在新增到圖中的時候形成了環，所以不能將v1和v2，v4和v5連起來。

普里姆演算法

方法:從指定頂點開始將它加入集合中,然後將集合內的頂點與集合外的頂點所構成的所有邊中選取權值最小的一條邊作為生成樹的邊,並將集合外的那個頂點加入到集合中,表示該頂點已連通.再用集合內的頂點與集合外的頂點構成的邊中找最小的邊,並將相應的頂點加入集合中,如此下去直到全部頂點都加入到集合中,即得最小生成樹.
例在下圖中從1點出發求出此圖的最小生成樹,並按生成樹的邊的順序將頂點與權值填入表中.

———————>先寫出其鄰接矩陣

第一步:從①開始，①進集合，用與集合外所有頂點能構成的邊中找最小權值的一條邊
①——②權6
①——③權1 -> 取①——③邊
①——④權5

第二步:③進集合，①，③與②,④,⑤,⑥構成的最小邊為
①——④權5
③——⑥權4 -> 取③——⑥邊

第三步:⑥進集合，①，③,⑥與②,④,⑤構成的各最小邊
①——②權6
③——②權5
⑥——④權2 -> 取⑥——④邊

第四步:④進集合，①，③,⑥,④與②,⑤構成的各最小邊
①——②權6
③——②權5 -> 取③——②邊
⑥——⑤權6

第四步:②進集合，①，③,⑥,②,④與⑤構成的各最小邊
②——⑤權3 -> 取②——⑤邊

這部分是轉載的:http://blog.csdn.net/weinierbian/article/details/8059129/

感覺簡單點就是直接找,1到3,3到6,6到4,然後沒法弄了,返回去找已經走過的結點,找最小的路,然後繼續走,走一下,找一下最小的(可能不對,不過我確實是這樣弄得)

對圖，分別給出使用普里姆演算法和克魯斯卡爾演算法生成最小生成樹的過程。