最小生成樹定義：

    給定一無向帶權圖，頂點數是n，要使圖連通只需n-1條邊，若這n-1條邊的權值和最小，則稱有這n個頂點和n-1條邊構成了圖的最小生成樹(minimum-cost spanning tree)MST。

兩種最小生成樹演算法：

一、prim演算法思想：設圖G頂點集合為U，首先任意選擇圖G中的一點作為起始點a，將該點加入集合V，再從集合U-V（差集）中找到另一點b使得點b到集合V中任意一點的權值最小，此時將b點也加入集合V；以此類推，現在的集合V={a，b}，再從集合U-V（差集）中找到另一點c使得點c到集合V中任意一點的權值最小，此時將c點加入集合V，直至所有頂點全部被加入V，此時就構建出了一顆MST。因為有N個頂點，所以該MST就有N-1條邊，每一次向集合V中加入一個點，就意味著找到一條MST的邊。

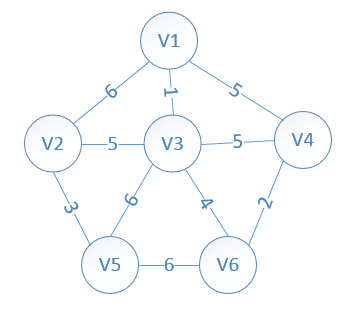
假設有一無向圖：

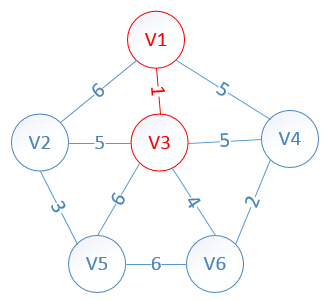
1、以v1作為起始點，初始時，V={v1}

2、從 U-V={v2,v3,v4,v5,v6}中選出到V={v1}中任意點最小權值點為v3,則V={v1,v3},則：

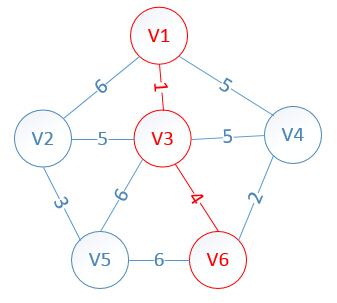
3、從 U-V={v2,v4,v5,v6}中選出到V={v1，v3}中任意點最小權值點為v6,則V={v1,v3，v6},則：

從 U-V={v2,v4,v5}中選出到V={v1，v3，v6}中任意點最小權值點為v4,則V={v1,v3，v6,v4},

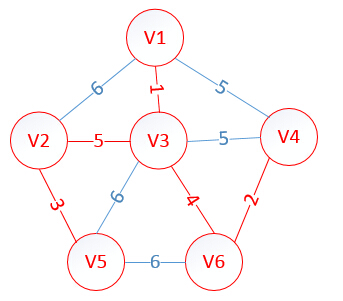
依此類推，在不能形成環路的條件下，依次選出：v2,v5,則最後的最小生成樹為：

二、kruskal演算法：

演算法思想：

圖中先將每個頂點看作獨立的子圖，然後查詢最小權值邊，這條邊是有限制條件的，邊得兩個頂點必須不在同一個子圖中，如上圖，第一次找到最小權值邊為（v1，v3），且滿足限制條件，繼續查詢到邊（v4，v6），（v2，v5），（v3，v6），當查詢到最後一條邊時，僅僅只有（v2，v3）滿足限制條件，其他的如（v3，v4），（v1，v4）都在一個子圖裡面，不滿足條件，至此已經找到最小生成樹的所有邊。

兩種演算法的C++實現：

.h檔案

#pragma once
#include <vector>
using namespace std;



/*   無向圖：
            A
         /  |  \
        B---F---E
		 \ / \ /
	      C---D

   索引: A B C D E F
         0 1 2 3 4 5

   權值：A-B 6、A-E 5、A-F 1
         B-C 3、B-F 2
		 C-F 8、C-D 7
		 D-F 4、D-E 2
		 E-F 9
*/


class CEdge//邊的類
{
public:
	CEdge(int NodeIndexA = 0,int NodeIndexB = 0,int WightValue = 0);
	int m_nNodeIndexA; //邊的起始點
	int m_nNodeIndexB;//邊的終點
	int m_nWeightValue;//邊的權值
	bool m_bSelected;//表明此邊是否被選擇過
};

class CNode//點的類
{
public:
	CNode(char cData = 0);
public:
	char m_cData;
	bool m_bIsVisited;
};

class CZzcGrapha
{
public:
	CZzcGrapha(int nCapacity);
	~CZzcGrapha(void);
	bool AddNodeToGrapha(CNode* pNode); //向圖中增加節點
	void ResetNodeVisitFlag();           //將所有節點的訪問標識置為false
	bool SetValueToMatrixForDirectedGraph(int row,int col,int value = 1);//向有向圖矩陣中設定值
	bool SetValueToMatrixForUnDirectedGraph(int row,int col,int value = 1);//向無向圖矩陣設定值
	bool GetValueFromMatrix(int row,int col,int& value);//從鄰接矩陣中獲取值
	void PrintMatrix();//打印出圖的鄰接矩陣
	void DepthFirstTraverse(int nodeindex);//深度優先遍歷
	void WidthFirstTraverse(int nodeindex);//廣度優先遍歷
	void WidthTraverseIteration(vector<int> prevec);

	void PrimTree(int nodeindex);//prim演算法 最小生成樹
	void Kruskal();//Kruskal 最小生成樹
private:
	int GetMinValueEdge(vector<CEdge> edgeVec);
	bool IsInSet(vector<int> nodeVec,int nodeIndex);
	void mergeNodeSet(vector<int> &nodeSetA,vector<int> nodeSetB);
private:
	int m_nCapacity;        //圖的容量（可以容納的節點數）
	int m_nCurNodeCount;    //圖中當前的節點個數
	CNode* m_pNodeArray;    //用來存放定點資料
	int* m_pMatrix;         //用來存放鄰接矩陣資料
	CEdge* m_pEdge;         //用來儲存找到的最小生成樹的邊
};

#include "StdAfx.h"
#include "ZzcGrapha.h"
#include "Windows.h"
#include <iostream>
using namespace std;


CEdge::CEdge(int NodeIndexA,int NodeIndexB,int WightValue)
{
	m_nNodeIndexA = NodeIndexA;
	m_nNodeIndexB = NodeIndexB;
	m_nWeightValue = WightValue;
	m_bSelected = false;
}

CNode::CNode(char cData)
{
	m_cData = cData;
	m_bIsVisited = false;
}

CZzcGrapha::CZzcGrapha(int nCapacity)
{
	m_nCapacity      = nCapacity;
	m_nCurNodeCount  = 0;
	m_pNodeArray     = new CNode[m_nCapacity];
	m_pMatrix        = new int[m_nCapacity * m_nCapacity];
	ZeroMemory(m_pMatrix,m_nCapacity * m_nCapacity * sizeof(int));

	m_pEdge = new CEdge[m_nCapacity - 1];
}

CZzcGrapha::~CZzcGrapha(void)
{
	if (m_pNodeArray)
	{
		delete[]m_pNodeArray;
		m_pNodeArray = NULL;
	}

	if (m_pMatrix)
	{
		delete[]m_pMatrix;
		m_pMatrix = NULL;
	}

	if (m_pEdge)
	{
		delete[]m_pEdge;
		m_pEdge = NULL;
	}
}

bool CZzcGrapha::AddNodeToGrapha(CNode* pNode)
{
	if(pNode == NULL) return false;

	m_pNodeArray[m_nCurNodeCount].m_cData = pNode->m_cData;
	m_nCurNodeCount++;
	return true;
}

void CZzcGrapha::ResetNodeVisitFlag()
{
	for(int i = 0;i < m_nCapacity;i++)
	{
		m_pNodeArray[i].m_bIsVisited = false;
	}
}

bool CZzcGrapha::SetValueToMatrixForDirectedGraph(int row,int col,int value)
{
	if(row < 0||row >= m_nCapacity) return false;

	if(col < 0||col >= m_nCapacity) return false;

	m_pMatrix[m_nCapacity * row + col] = value;

	return true;
}

bool CZzcGrapha::SetValueToMatrixForUnDirectedGraph(int row,int col,int value)
{
	if(row < 0||row >= m_nCapacity) return false;

	if(col < 0||col >= m_nCapacity) return false;

	m_pMatrix[m_nCapacity * row + col] = value;
	m_pMatrix[m_nCapacity * col + row] = value;

	return true;
}

bool CZzcGrapha::GetValueFromMatrix(int row,int col,int& value)
{
	if(row < 0||row >= m_nCapacity) return false;

	if(col < 0||col >= m_nCapacity) return false;

	value = m_pMatrix[m_nCapacity * row + col];

	return true;
}

void CZzcGrapha::PrintMatrix()
{
	for (int i = 0;i < m_nCapacity;i++)
	{
		for (int k = 0;k < m_nCapacity;k++)
		{
			cout<<m_pMatrix[m_nCapacity * i + k]<<" "; 
		}

		cout<<endl;
	}
}

void CZzcGrapha::DepthFirstTraverse(int nodeindex)
{
	int value = 0;

	cout<<m_pNodeArray[nodeindex].m_cData<<" ";
	m_pNodeArray[nodeindex].m_bIsVisited = true;

	for (int i = 0;i < m_nCapacity;i++)
	{
		GetValueFromMatrix(nodeindex,i,value);

		if (value == 1)
		{
			if(m_pNodeArray[i].m_bIsVisited == true) continue;

			DepthFirstTraverse(i);
		} 
		else
		{
			continue;
		}
	}
}

void CZzcGrapha::WidthFirstTraverse(int nodeindex)
{
	cout<<m_pNodeArray[nodeindex].m_cData<<" ";
	m_pNodeArray[nodeindex].m_bIsVisited = true;

	vector<int> curVec;
	curVec.push_back(nodeindex);
	WidthTraverseIteration(curVec);
}

void CZzcGrapha::WidthTraverseIteration(vector<int> prevec)
{
	int value = 0;

	vector<int> curVec;

	for(int i = 0;i < (int)prevec.size();i++)
	{
		for (int j = 0;j < m_nCapacity;j++)
		{
			GetValueFromMatrix(prevec[i],j,value);

			if (value != 0)
			{
				if(m_pNodeArray[j].m_bIsVisited) continue;

				cout<<m_pNodeArray[j].m_cData<<" ";
				m_pNodeArray[j].m_bIsVisited = true;

				curVec.push_back(j);
			} 
			else
			{
				continue;
			}
		}
	}

	if(curVec.size() == 0) return;

	WidthTraverseIteration(curVec);
}

//引數nodeindex表示第一個加入到點集合中的點
void CZzcGrapha::PrimTree(int nodeindex)//prim演算法 最小生成樹
{
	int value = 0;//存放所取得的邊的權值
	int edgeCount = 0;//標識所找到的邊的數目
	vector<int> nodeVec;//存放所找到的點的索引的集合
	vector<CEdge> edgeVec;//存放所找到的邊的集合

	nodeVec.push_back(nodeindex);//將第一個點的索引加入到點集合
	m_pNodeArray[nodeindex].m_bIsVisited = true;//第一個點已經被訪問過了

	cout<<m_pNodeArray[nodeindex].m_cData<<endl;

	while (edgeCount < m_nCapacity - 1)
	{
		int temp = nodeVec.back();

		for (int i = 0;i < m_nCapacity;i++)//尋找與temp點相連線的點
		{
			GetValueFromMatrix(temp,i,value);

			if (value != 0)//權值不為0，則兩點相連線
			{
				if (m_pNodeArray[i].m_bIsVisited)//此點已經被訪問過了
				{
					continue;
				} 
				else
				{
					CEdge edge(temp,i,value);//構造temp與i兩點之間的邊
					edgeVec.push_back(edge);//將此邊加入到邊的集合
				}
			}
		}

		//for迴圈過後會找到與temp點連線的所有的邊，下面找到權值最小的邊,返回此邊在集合中的索引

		int mixEdgeIndex = GetMinValueEdge(edgeVec);

		edgeVec[mixEdgeIndex].m_bSelected = true;

		cout<<edgeVec[mixEdgeIndex].m_nNodeIndexA<<"---"<<edgeVec[mixEdgeIndex].m_nNodeIndexB<<"   ";
		cout<<edgeVec[mixEdgeIndex].m_nWeightValue<<endl;
		cout<<m_pNodeArray[edgeVec[mixEdgeIndex].m_nNodeIndexB].m_cData<<endl;

		m_pEdge[edgeCount] = edgeVec[mixEdgeIndex];//儲存找到的最小邊

		edgeCount++;

		int nextNodeIndex = edgeVec[mixEdgeIndex].m_nNodeIndexB;//下次要加入到點集合中的索引

		nodeVec.push_back(nextNodeIndex);

		m_pNodeArray[nextNodeIndex].m_bIsVisited = true;
	}
}

int CZzcGrapha::GetMinValueEdge(vector<CEdge> edgeVec)//找到最小權值邊
{
	int value = 0;
	int edgeIndex = 0;
	
	int i = 0;

	for (;i < (int)edgeVec.size();i++)
	{
		if (!edgeVec[i].m_bSelected)
		{
			value = edgeVec[i].m_nWeightValue;
			edgeIndex = i;
			break;
		}
	}

	if (value == 0)
	{
		return -1;
	}

	for (;i < (int)edgeVec.size();i++)
	{
		if(edgeVec[i].m_bSelected) continue;

		if (value > edgeVec[i].m_nWeightValue)
		{
			value = edgeVec[i].m_nWeightValue;
			edgeIndex = i;
		}
	}

	return edgeIndex;
}

void CZzcGrapha::Kruskal()
{
	int value = 0,edgeCount = 0;

	vector<vector<int>> nodeSets;//存放點集合的陣列，相當於是陣列的陣列

	vector<CEdge> edgeVec;//存放邊的陣列

	//第一步：找出所有邊，並放入到邊的陣列中
	for (int i = 0;i < m_nCapacity - 1;i++)
	{
		for (int k = i + 1;k < m_nCapacity;k++)
		{
			GetValueFromMatrix(i,k,value);
			cout<<value<<" ";
			
			if (value != 0)//i和k兩個點之間存在邊
			{
				

				CEdge edge(i,k,value);
				edgeVec.push_back(edge);
			}
		}
		cout<<endl;
	}

	//第二步，從所有邊中取出最小生成樹的邊
	while (edgeCount < m_nCapacity - 1)
	{
		//從邊的集合中找出最小邊
		int minEdgeIndex = GetMinValueEdge(edgeVec);
		edgeVec[minEdgeIndex].m_bSelected = true;

		//取出最小邊的兩個點
		int nodeAIndex = edgeVec[minEdgeIndex].m_nNodeIndexA;
		int nodeBIndex = edgeVec[minEdgeIndex].m_nNodeIndexB;

		bool bNodeAIsInSet = false;
		bool bNodeBIsInSet = false;

		int nNodeAInSetLab = -1;
		int nNodeBInSetLab = -1;

		//分別找出最小邊兩個點所在的集合
		for (int i = 0;i < (int)nodeSets.size();i++)
		{
			bNodeAIsInSet = IsInSet(nodeSets[i],nodeAIndex);//判斷nodeAIndex點在哪個點集合中

			if (bNodeAIsInSet)
			{
				nNodeAInSetLab = i;//將集合索引儲存起來
			}
		}

		for (int i = 0;i < (int)nodeSets.size();i++)
		{
			bNodeBIsInSet = IsInSet(nodeSets[i],nodeBIndex);//判斷nodeAIndex點在哪個點集合中

			if (bNodeBIsInSet)
			{
				nNodeBInSetLab = i;//將集合索引儲存起來
			}
		}

		//兩點都不在已經存在的集合中,新建一個集合放入集合的陣列中
		if(nNodeAInSetLab == -1&&nNodeBInSetLab == -1)
		{
			vector<int> vec;
			vec.push_back(nodeAIndex);
			vec.push_back(nodeBIndex);
			nodeSets.push_back(vec);
		}
		//nodeAIndex不在已經存在的集合中，nodeBIndex在已經存在的集合中，
		//將nodeAIndex放入到nodeBIndex所在的集合中
		else if(nNodeAInSetLab == -1&&nNodeBInSetLab != -1)
		{
			nodeSets[nNodeBInSetLab].push_back(nodeAIndex);
		}
		//nodeAIndex在已經存在的集合中，nodeBIndex不在已經存在的集合中，
		//將nodeBIndex放入到nodeAIndex所在的集合中
		else if(nNodeAInSetLab != -1&&nNodeBInSetLab == -1)
		{
			nodeSets[nNodeAInSetLab].push_back(nodeBIndex);
		}
		//兩點在不同的集合中，合併兩個集合
		else if(nNodeAInSetLab != -1&&nNodeBInSetLab != -1&&nNodeAInSetLab != nNodeBInSetLab)
		{
			//引數2合併到引數1的集合中
			mergeNodeSet(nodeSets[nNodeAInSetLab],nodeSets[nNodeBInSetLab]);
			//將引數2集合從nodeSets集合中去掉
			for (int i = nNodeBInSetLab;i < (int)nodeSets.size()-1;i++)
			{
				nodeSets[i] = nodeSets[i+1];
			}
		}
		//當期的兩個點在同一個集合中，這就會形成迴路，多以當期邊要摒棄掉
		else if(nNodeAInSetLab != -1&&nNodeBInSetLab != -1&&nNodeAInSetLab == nNodeBInSetLab)
		{
			continue;
		}
		//到這裡說明找出的邊符合要求，將此邊儲存起來
		m_pEdge[edgeCount] = edgeVec[minEdgeIndex];
		edgeCount++;

		cout<<edgeVec[minEdgeIndex].m_nNodeIndexA<<"---"<<edgeVec[minEdgeIndex].m_nNodeIndexB<<"   ";
		cout<<edgeVec[minEdgeIndex].m_nWeightValue<<endl;
	}
}

bool CZzcGrapha::IsInSet(vector<int> nodeVec,int nodeIndex)
{
	for (int i = 0;i < (int)nodeVec.size();i++)
	{
		if (nodeVec[i] == nodeIndex)
		{
			return true;
		}
	}

	return false;
}

void CZzcGrapha::mergeNodeSet(vector<int> &nodeSetA,vector<int> nodeSetB)
{
	for (int i = 0;i < (int)nodeSetB.size();i++)
	{
		nodeSetA.push_back(nodeSetB[i]);
	}
}

// 圖.cpp : 定義控制檯應用程式的入口點。
//

#include "stdafx.h"
#include "ZzcGrapha.h"
#include <iostream>
using namespace std;


int _tmain(int argc, _TCHAR* argv[])
{
	CZzcGrapha* pGrapha = new CZzcGrapha(6);

	CNode* pNodeA = new CNode('A');
	CNode* pNodeB = new CNode('B');
	CNode* pNodeC = new CNode('C');
	CNode* pNodeD = new CNode('D');
	CNode* pNodeE = new CNode('E');
	CNode* pNodeF = new CNode('F');

	pGrapha->AddNodeToGrapha(pNodeA);
	pGrapha->AddNodeToGrapha(pNodeB);
	pGrapha->AddNodeToGrapha(pNodeC);
	pGrapha->AddNodeToGrapha(pNodeD);
	pGrapha->AddNodeToGrapha(pNodeE);
	pGrapha->AddNodeToGrapha(pNodeF);

	pGrapha->SetValueToMatrixForUnDirectedGraph(0,1,6);
	pGrapha->SetValueToMatrixForUnDirectedGraph(0,4,5);
	pGrapha->SetValueToMatrixForUnDirectedGraph(0,5,1);
	pGrapha->SetValueToMatrixForUnDirectedGraph(1,2,3);
	pGrapha->SetValueToMatrixForUnDirectedGraph(1,5,2);
	pGrapha->SetValueToMatrixForUnDirectedGraph(2,5,8);
	pGrapha->SetValueToMatrixForUnDirectedGraph(2,3,7);
	pGrapha->SetValueToMatrixForUnDirectedGraph(3,5,4);
	pGrapha->SetValueToMatrixForUnDirectedGraph(3,4,2);
	pGrapha->SetValueToMatrixForUnDirectedGraph(4,5,9);

	pGrapha->PrintMatrix();
	cout<<endl;

	//pGrapha->DepthFirstTraverse(0);
	//cout<<endl;
	//pGrapha->ResetNodeVisitFlag();
	//pGrapha->WidthFirstTraverse(0);

	//pGrapha->PrimTree(0);
	pGrapha->Kruskal();


	return 0;
}