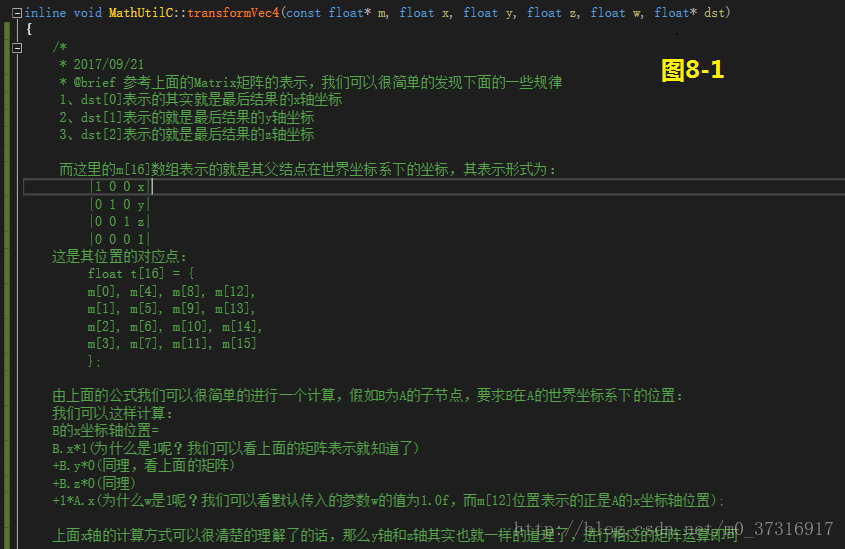
[cocos2d-x]從原始碼角度思考convertToWorldSpace()與convertToWorldSpaceAR()座標系的轉換
convertToWorldSpace()
話不多說,先上原始碼,之後再慢慢講解:

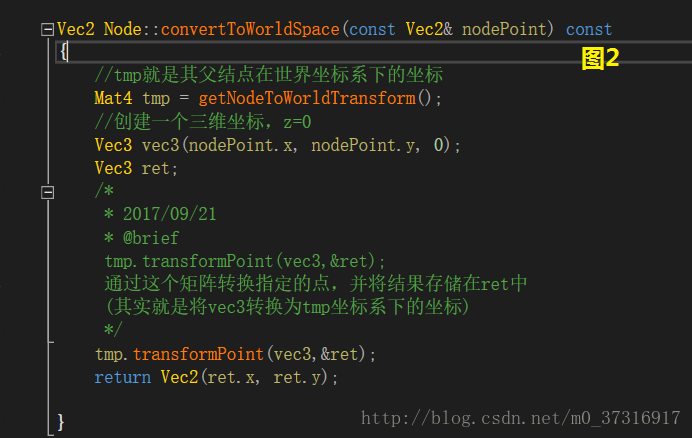
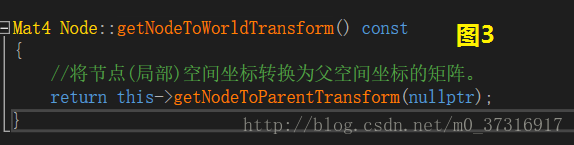
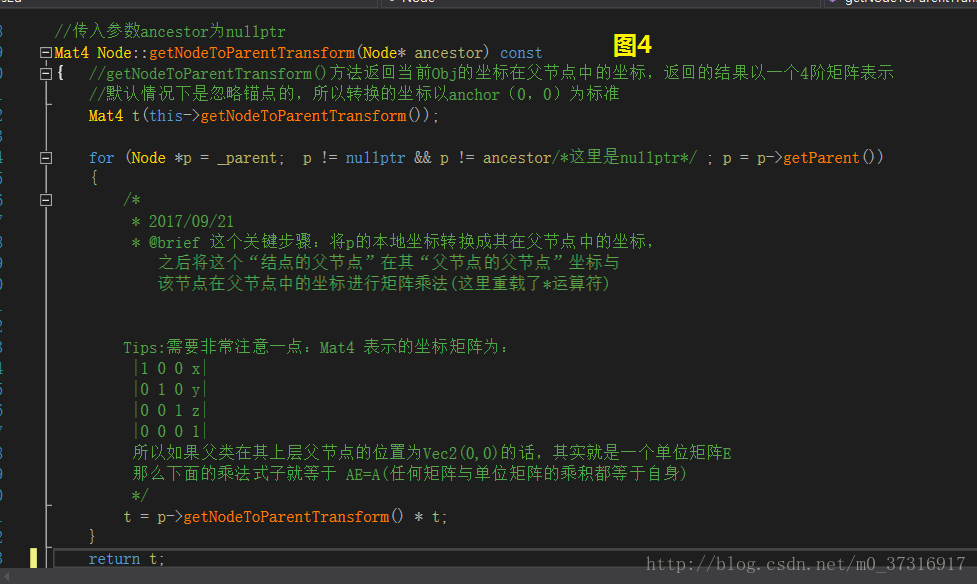
(5和6圖截圖的時候重複了,這裡就不弄出來了)
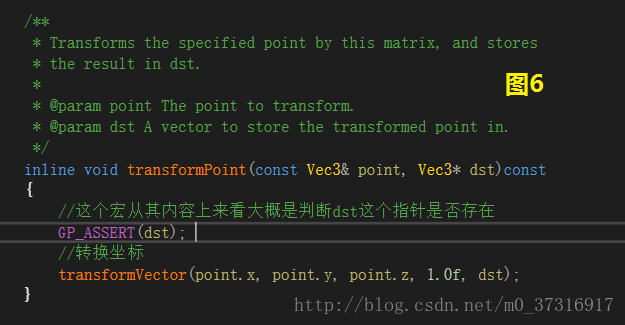


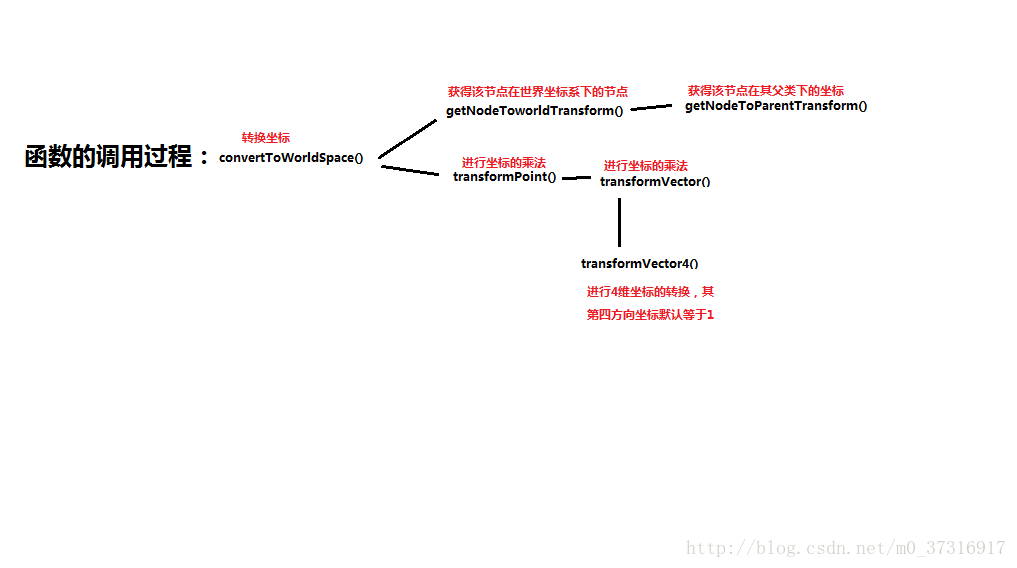
只要通過圖1到圖8中我寫的註釋進行分析(不懂的地方可以自己去翻一下cocos2dx的原始碼,這樣可能更直接)
所以結論就很明顯:最後的結果=子節點在父節點中的座標+父節點在世界座標系下的座標
convertToWorldSpaceAR()
當然,我們由此也可以來看下convertToWorldSpaceAR()的實現:


從圖中的原始碼,我們其實很好理解,就是將子節點在父節點中的座標加上父節點的錨點(以畫素為單位的錨點)
最後的結論就是:最後的座標=子節點在父節點中的座標+父節點在世界座標系下的座標+父節點的錨點(以畫素為單位,也就是anchorPoint*ContentSize())
一個簡單的例子來驗證
這個例子是我從cocos2dx-lua實戰書中看到的,從圖中的結果我們可以看到轉換後的座標的計算方式:
convertToWorldSpace():
最後座標(250,450)=(0,0)+(250,450)
convertToWorldSpace():
最後座標(400,500)=(0,0)+(250,450)+(0.5,0.5)×(300,100)
最後下個總結
convertToWorldSpace():最後的結果=子節點在父節點中的座標+父節點在世界座標系下的座標
convertToWorldSpace():最後的座標=子節點在父節點中的座標+父節點在世界座標系下的座標+父節點的錨點(以畫素為單位,也就是anchorPoint*ContentSize())
總結中的總結:
雖然convertToNodeSpace()和convertToNodeSpaceAR()沒有分析,但是我想實現的過程應該是差不多相反的過程,下次有時間再去看一下原始碼。
好吧,其實通過分析這個原始碼,我還是沒有從底層的原理上透徹理解座標儲存在矩陣中所進行的矩陣運算的原理,比如下面幾個問題都還困擾著我:
為什麼要將其座標軸儲存在其對應的位置並且還要加上一個單位矩陣?
四維向量中第四個向量代表的是什麼意思?
父節點和子節點之間的座標矩陣乘法的原理是什麼,為什麼要這樣乘呢?
and so on….
這些答案可能還需要以後進一步的學習才理解,共勉!